Производная степенной функции. Ее геометрический смысл

Задачи урока:
1 Применяя геометрический смысл производной находить:
а) Угловой коэффициент касательной к графику функции.
б) Угол ,образованный касательной к графику функции с положительным направлением оси абсцисс.
в) Тангенс угла наклона касательной.
2 Исследовать функцию на монотонность. Находить наименьшее и наибольшее значение функции на промежутке.

Найти наименьшее и наибольшее значение функции
На промежутке [1; 2]
На промежутке (6; 8]
Решение: Функция является возрастающей на D(y) , значит большему значению аргумента соответствует большее значение функции.
Решение: Наименьшего не существует.

на [1;8]
Ответ :
№ 38.32(а,б)
Правило.
Найти значение функции на концах отрезка f(а) и f(b)
Найти ее значения в тех критических точках, которые принадлежат интервалу (а;b)
Из найденных значений выбрать наибольшее и наименьшее.
Наибольшее значение на интервале функция принимает в точке максимума , наименьшее- в точке минимума.

Найти наименьшее и наибольшее значение заданной функции на заданном промежутке:
Ответ: Наибольшее 0, наименьшее значение -8/3
Ответ: Наибольшее ½, наименьшее не существует.

Геометрический смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.
Найдите угловой коэффициент касательной к графику функции y=f(х) в точке с абсциссой х=1
Найдите угол, образованный касательной к графику функции y=f(x) с положительным направлением оси абсцисс в точке.
Найдите тангенс угла наклона касательной, проведенной к графику функции y=f(x) в его точке с абсциссой x=-1

Установим связь между условием и заключением.
Задача1
Задача 2,3

Решите уравнение.
Проведите касательную к графику заданной функции из данной точки М(0;1)

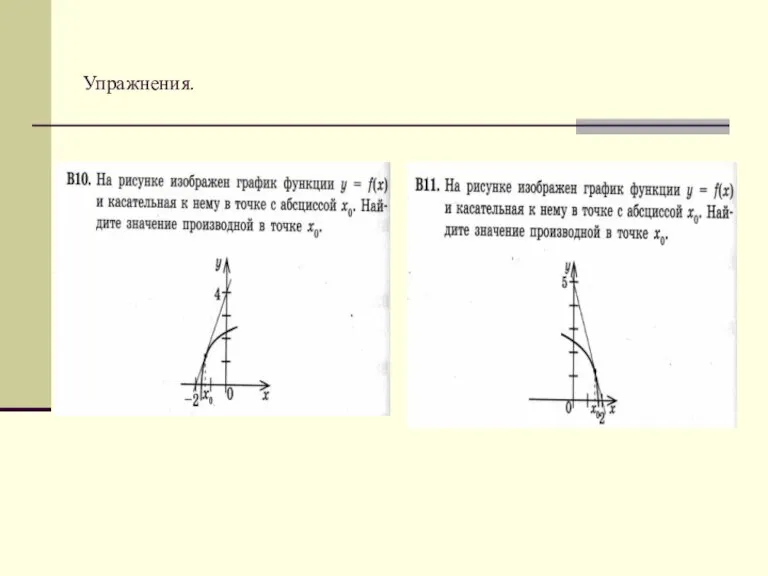
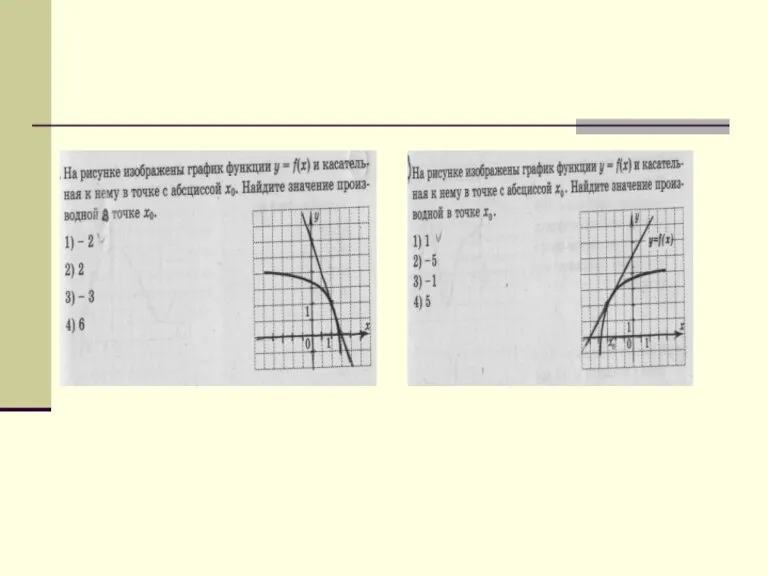
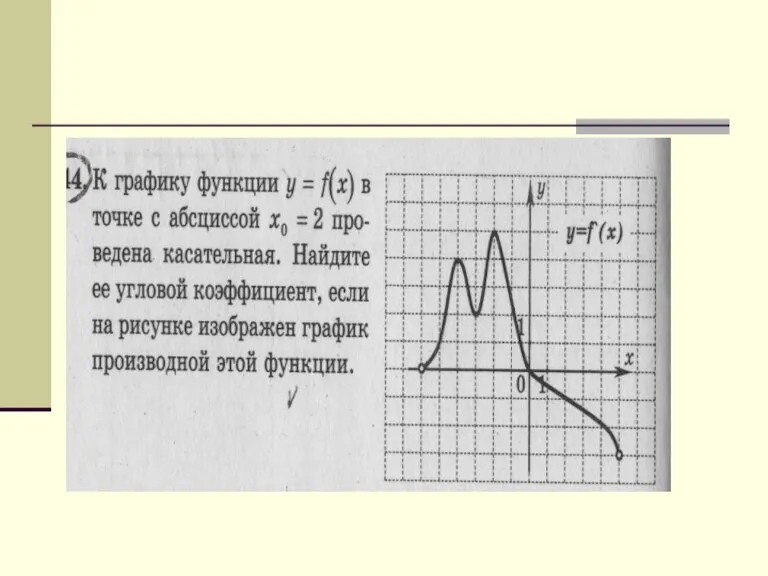
Упражнения.

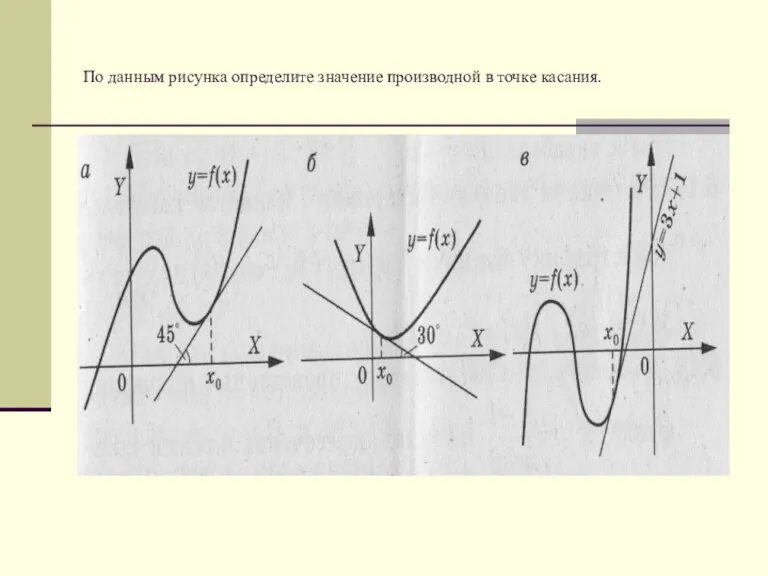
По данным рисунка определите значение производной в точке касания.

Итог урока: Руководство к решению задачи.
1) Понять смысл задания.
2)Установить связь между условием и заключением.
3)Применить необходимые формулы.
4)Самоконтроль выполнения.