Слайд 2Справимся легко!
№1. По графику функции y=f(x) ответьте на вопросы:
Сколько точек максимума имеет
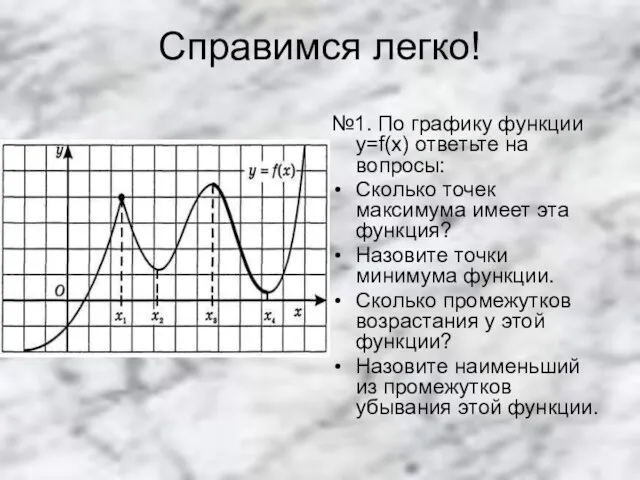
эта функция?
Назовите точки минимума функции.
Сколько промежутков возрастания у этой функции?
Назовите наименьший из промежутков убывания этой функции.
Слайд 3Легко ли?
№2. (задание В5 ЕГЭ по математике)
По графику функции
y=f ´(x) ответьте
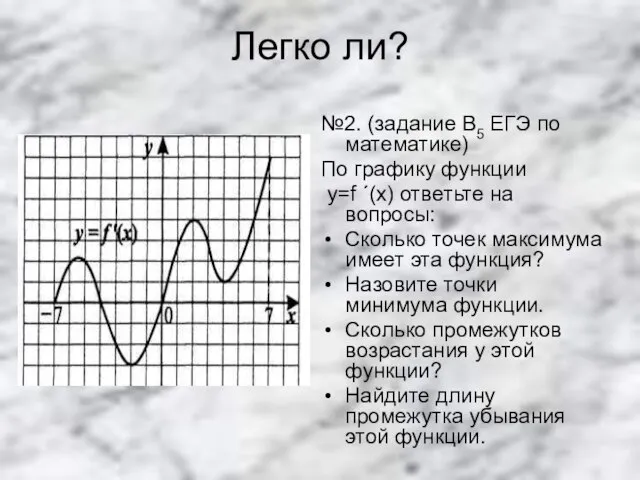
на вопросы:
Сколько точек максимума имеет эта функция?
Назовите точки минимума функции.
Сколько промежутков возрастания у этой функции?
Найдите длину промежутка убывания этой функции.
Слайд 4Для нас задача…
Составить (создать, разработать) правило (алгоритм), с помощью которого

можно исследовать функции на монотонность и экстремумы по её производной.
Слайд 7Теорема 1
Если во всех точках открытого промежутка Х производная f ´(x)

больше или равна нулю (причем
f ´(x) =0 лишь в отдельных точках), то функция y=f (x) возрастает на промежутке Х.
Слайд 8Теорема 2
Если во всех точках открытого промежутка Х производная f ´(x)

меньше или равна нулю (причем
f ´(x) =0 лишь в отдельных точках), то функция y=f (x) убывает
на промежутке Х.
Слайд 9Теорема 3
Если функция y=f (x) имеет экстремум в точке х0, то

в этой точке производная функции либо равна нулю, либо не существует.
Слайд 11
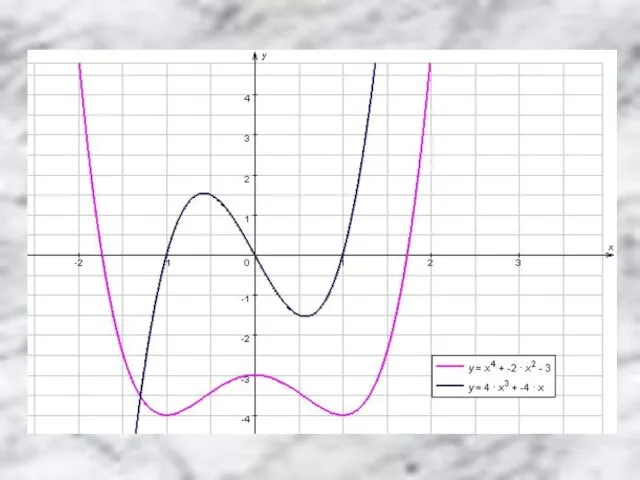
№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её
![№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/304456/slide-10.jpg)
производной. Укажите количество промежутков возрастания функции.
Слайд 12 №2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график
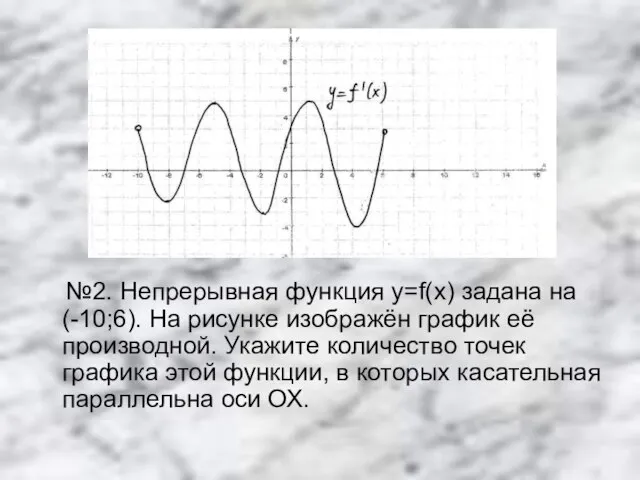
её производной. Укажите количество точек графика этой функции, в которых касательная параллельна оси ОХ.
Слайд 13 №3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график
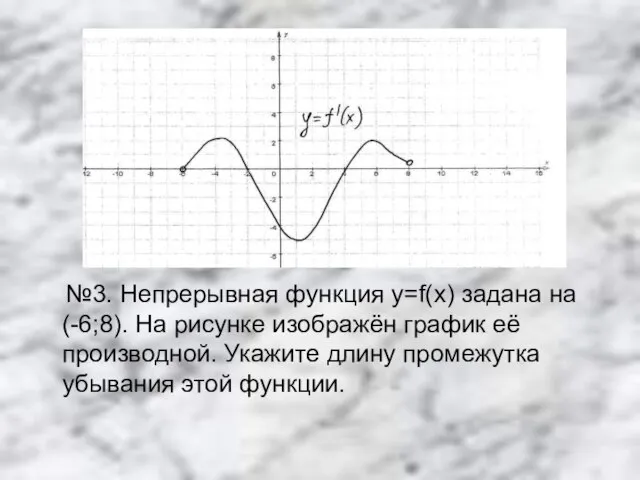
её производной. Укажите длину промежутка убывания этой функции.








![№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/304456/slide-10.jpg)


 Виды показательных уравнений
Виды показательных уравнений  Путешествие в страну дробных чисел
Путешествие в страну дробных чисел Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Старая сказка на новый лад
Старая сказка на новый лад ТОЖДЕСТВА 7 класс
ТОЖДЕСТВА 7 класс  Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_
Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_ 9-klass-kvadratichnaya-funkciya.ppt
9-klass-kvadratichnaya-funkciya.ppt Метод рационализации
Метод рационализации Графическое решение систем уравнений
Графическое решение систем уравнений Презентация на тему Аварии на радиационно-опасных объектах
Презентация на тему Аварии на радиационно-опасных объектах  Сложение и вычитание смешанных чисел 5 класс
Сложение и вычитание смешанных чисел 5 класс Всё о квадратном уравнении
Всё о квадратном уравнении Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766
Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766 Квадратный трехчлен и его приложения
Квадратный трехчлен и его приложения Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Алгебра модуля
Алгебра модуля Построение арифметических выражений
Построение арифметических выражений Uravneniya-s-parametrami.ppt
Uravneniya-s-parametrami.ppt Обратные тригонометрические функции
Обратные тригонометрические функции vzaimno-obratnye-funkcii.ppt
vzaimno-obratnye-funkcii.ppt Комбинаторные задачи Перестановки РазмещенияСочетания (выборки)
Комбинаторные задачи Перестановки РазмещенияСочетания (выборки) Арифметическая прогрессия.Формула n –го члена арифметической прогрессии
Арифметическая прогрессия.Формула n –го члена арифметической прогрессии Как появилось книгопечатание на Руси
Как появилось книгопечатание на Руси Свойства функций
Свойства функций Одночлены и многочлены 7 класс
Одночлены и многочлены 7 класс Презентация на тему Экзамен без стресса
Презентация на тему Экзамен без стресса  Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений