Слайд 2Задача №1.
На одной полке книжного шкафа стоит 30 различных книг, а на

другой – 40 различных книг (не такие как на первой). Сколькими способами можно выбрать одну книгу.
Решение:
30 + 40 = 70 (способами).
Слайд 3Правило суммы
Если пересечение конечных множеств А и В пусто, то число элементов

в их объединении равно сумме чисел элементов множеств А и В :
Слайд 4Задача № 2
При формировании экипажа космического корабля имеется 10 претендентов на пост

командира, 20 – на пост инженера и 25 – на пост космонавта. Сколькими способами можно выбрать одну из кандидатур или командира, или инженера, или космонавта, если не один кандидат не претендует одновременно на два поста?
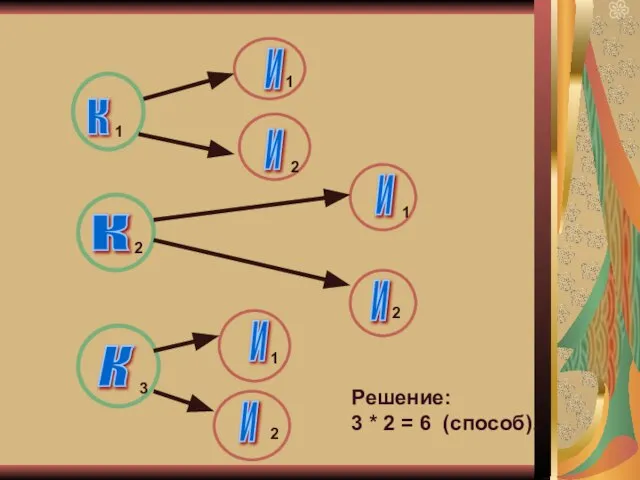
Слайд 5Задача № 3
Пусть существует три кандидата на пост командира и 2 на

пост инженера. Сколькими способами можно сформировать экипаж корабля, состоящий из командира и инженера?
Слайд 6к
к
к
и
и
и
и
и
и
1
1
1
1
2
3
2
2
2
Решение:
3 * 2 = 6 (способ).
Слайд 7Правило умножения.
Если множества А и В конечны, то число N возможных пар

(а; в), где а из А, в из В равно произведению чисел элементов этих множеств:
N = n (A) *n (B)
Слайд 8Задача № 2
Сколькими способами можно выбрать в столовой обед из трех блюд

из предложенных двух первых, трех вторых блюд и двух видов десерта.







 Виды показательных уравнений
Виды показательных уравнений  Путешествие в страну дробных чисел
Путешествие в страну дробных чисел Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Старая сказка на новый лад
Старая сказка на новый лад ТОЖДЕСТВА 7 класс
ТОЖДЕСТВА 7 класс  Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_
Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_ 9-klass-kvadratichnaya-funkciya.ppt
9-klass-kvadratichnaya-funkciya.ppt Метод рационализации
Метод рационализации Графическое решение систем уравнений
Графическое решение систем уравнений Презентация на тему Аварии на радиационно-опасных объектах
Презентация на тему Аварии на радиационно-опасных объектах  Сложение и вычитание смешанных чисел 5 класс
Сложение и вычитание смешанных чисел 5 класс Всё о квадратном уравнении
Всё о квадратном уравнении Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766
Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766 Квадратный трехчлен и его приложения
Квадратный трехчлен и его приложения Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Алгебра модуля
Алгебра модуля Построение арифметических выражений
Построение арифметических выражений Uravneniya-s-parametrami.ppt
Uravneniya-s-parametrami.ppt Обратные тригонометрические функции
Обратные тригонометрические функции vzaimno-obratnye-funkcii.ppt
vzaimno-obratnye-funkcii.ppt Комбинаторные задачи Перестановки РазмещенияСочетания (выборки)
Комбинаторные задачи Перестановки РазмещенияСочетания (выборки) Арифметическая прогрессия.Формула n –го члена арифметической прогрессии
Арифметическая прогрессия.Формула n –го члена арифметической прогрессии Как появилось книгопечатание на Руси
Как появилось книгопечатание на Руси Свойства функций
Свойства функций Одночлены и многочлены 7 класс
Одночлены и многочлены 7 класс Презентация на тему Экзамен без стресса
Презентация на тему Экзамен без стресса  Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений