Тригонометрические функции и их графики

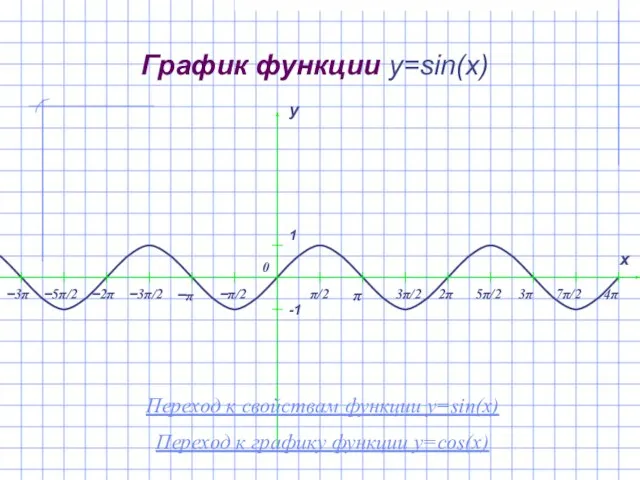
График функции y=sin(x)
Переход к свойствам функции y=sin(x)
Переход к графику функции y=cos(x)

Свойства функции y=sin(x)
Область определения y=sin(x) – множество R всех действительных чисел.
Множество значений y=sin(x) – отрезок [-1;1].
Функция периодическая: sin(x)=sin(x+2πn) , n∈Ζ.
Функция нечётная: sin(x)=-sin(-x).
Функция принимает нулевые значения в точках, кратных π.
Функция y=sin(x) принимает максимальное значение, равное 1, в точках x=π/2 + 2πn, n∈Ζ.
Функция y=sin(x) принимает минимальное значение, равное -1 в точках x=-π/2 + 2πn , n∈Ζ.
Между этими точками функция y=sin(x) монотонно убывает или монотонно возрастает.
Вернись обратно к графику и найди на нём все указанные свойства функции y=sin(x) !

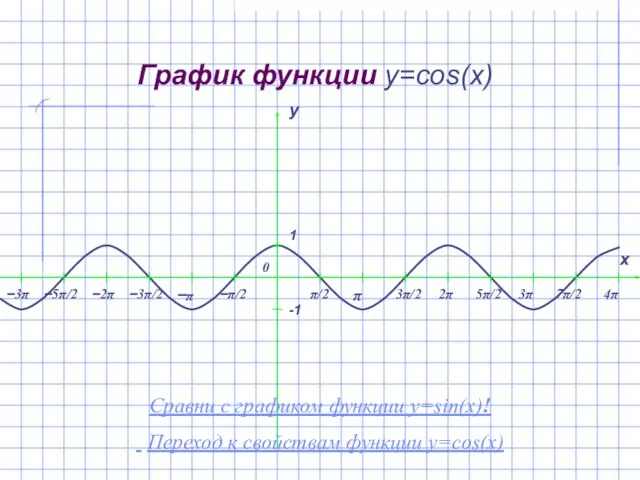
График функции y=cos(x)
Сравни с графиком функции y=sin(x)!
Переход к свойствам функции y=cos(x)

Свойства функции y=cos(x)
Область определения y=cos(x) – множество R всех действительных чисел.
Множество значений y=cos(x) – отрезок [-1;1].
Функция периодическая: cos(x)=cos(x+2πn) , n ∈Ζ.
Функция чётная: cos(x)=cos(-x).
Функция y=cos(x) принимает нулевые значения в точках x=π/2 + πn , n ∈Ζ.
Функция y=cos(x) принимает максимальное значение, равное 1, в точках x=2πn , n ∈Ζ.
Функция y=cos(x) принимает минимальное значение, равное -1 в точках x= (2n+1 ) π, n ∈ Ζ.
Между этими точками функция y=cos(x) монотонно убывает или монотонно возрастает.
Вернись обратно к графику и найди на нём все указанные свойства функции y=cos(x) !

Преобразования графиков функций sin(x) и cos(x)
y= -sin(x)
y= sin(x-)
y= sin(x+/2)
y= sin(x-/4)
y= sin(x)+2
y= 2sin(x)-1
y= 2sin(x-/4)-1
y= -cos(x)
y= cos(x+)
y= cos(x-/2)
y= cos(x+/4)
y= cos(x)-1
y= 2cos(x)+1
y= 2cos(x+/4)+1

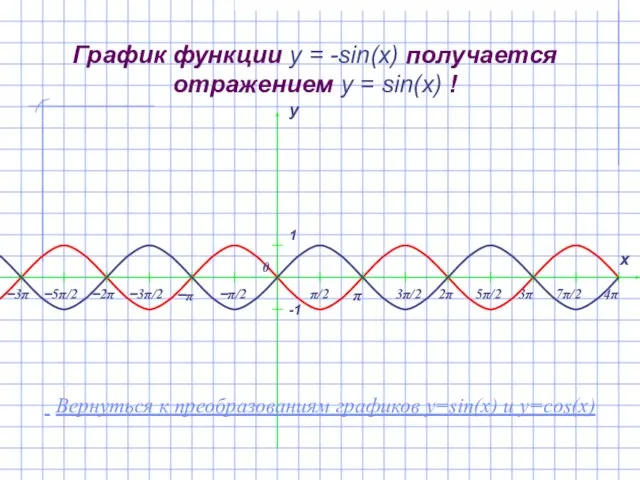
График функции y = -sin(x) получается отражением y = sin(x) !
Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

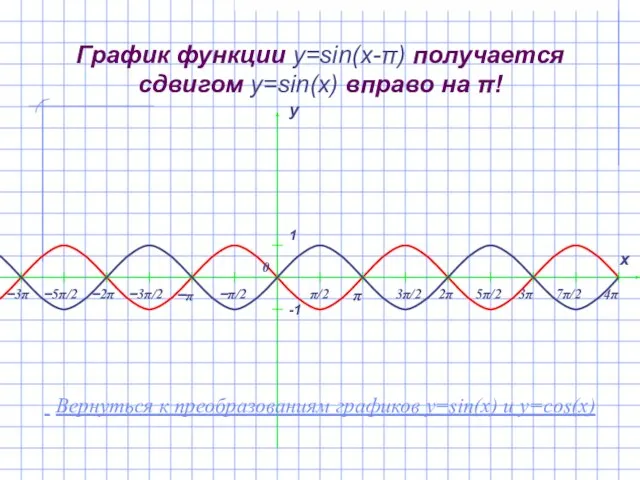
График функции y=sin(x-π) получается сдвигом y=sin(x) вправо на π!
Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

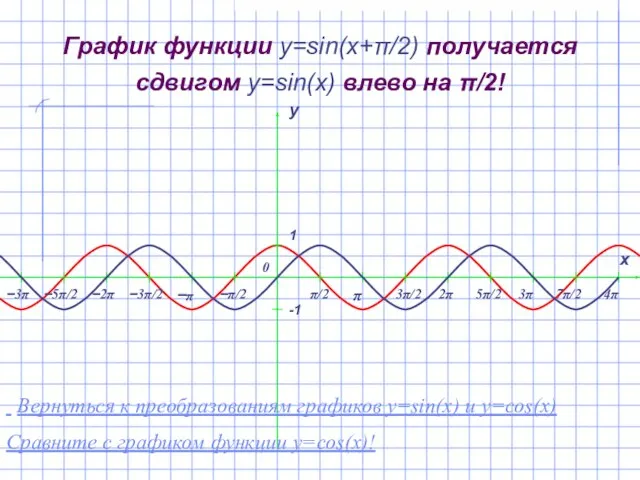
График функции y=sin(x+π/2) получается сдвигом y=sin(x) влево на π/2!
Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)
Сравните с графиком функции y=cos(x)!

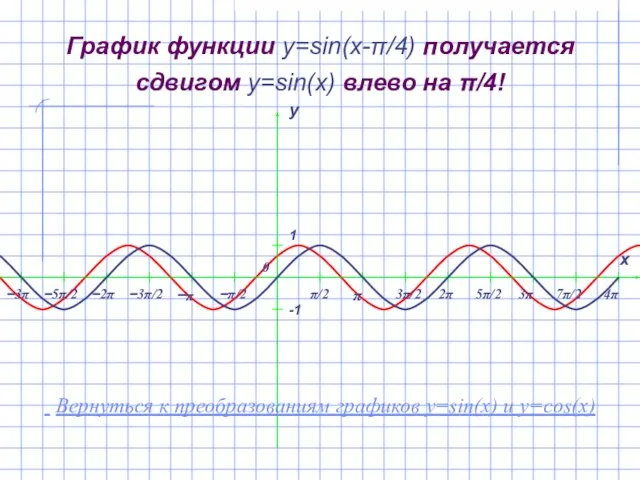
График функции y=sin(x-π/4) получается сдвигом y=sin(x) влево на π/4!
Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

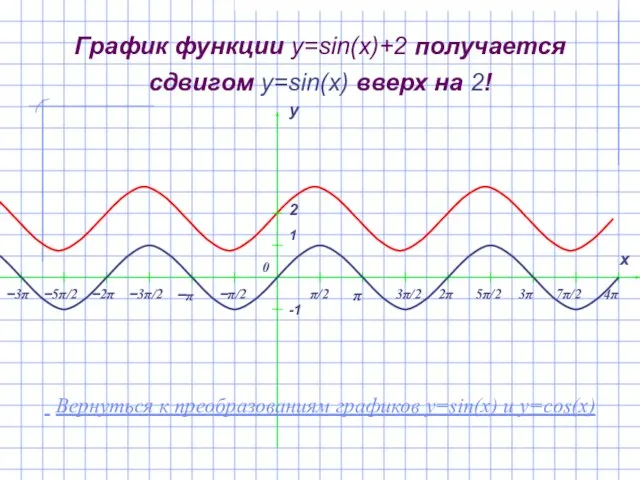
График функции y=sin(x)+2 получается сдвигом y=sin(x) вверх на 2!
Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

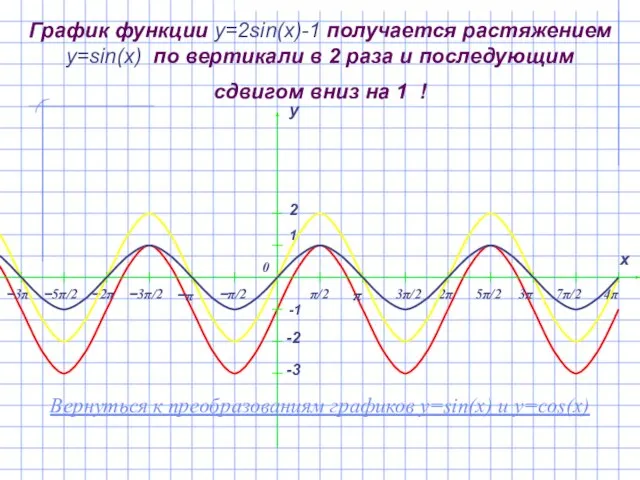
График функции y=2sin(x)-1 получается растяжением y=sin(x) по вертикали в 2 раза и последующим сдвигом вниз на 1 !
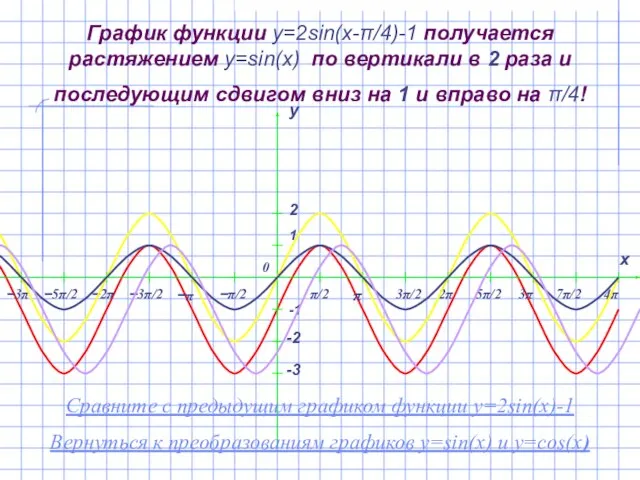
Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

График функции y=2sin(x-π/4)-1 получается растяжением y=sin(x) по вертикали в 2 раза и последующим сдвигом вниз на 1 и вправо на π/4!
Сравните с предыдущим графиком функции y=2sin(x)-1
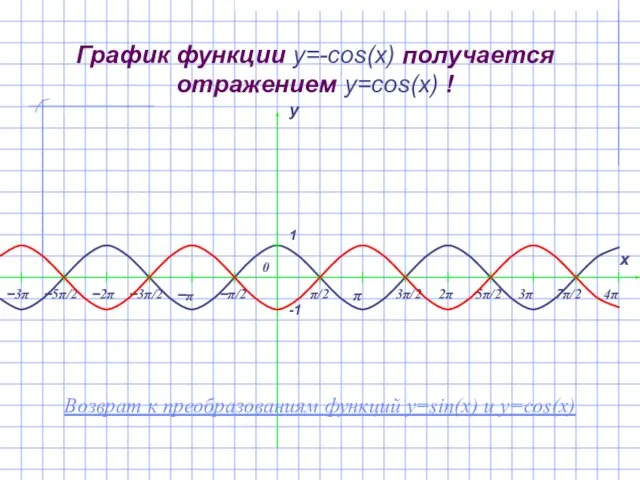
Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

График функции y=-cos(x) получается отражением y=cos(x) !
Возврат к преобразованиям функций y=sin(x) и y=cos(x)

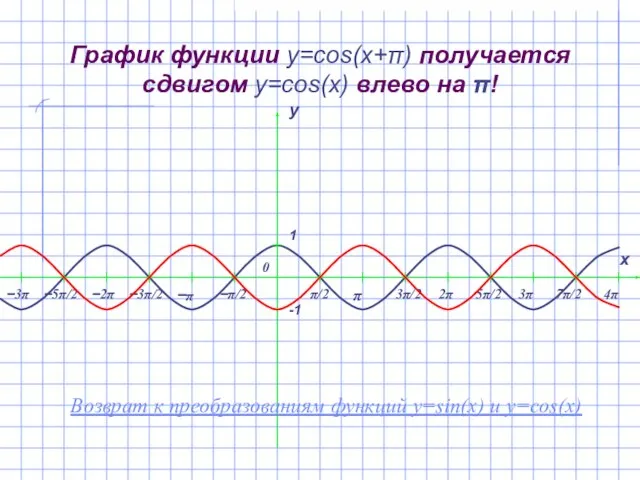
График функции y=cos(x+π) получается сдвигом y=cos(x) влево на π!
Возврат к преобразованиям функций y=sin(x) и y=cos(x)

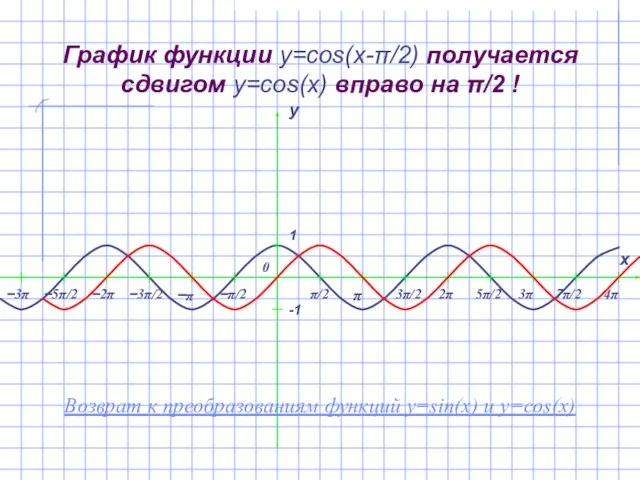
График функции y=cos(x-π/2) получается сдвигом y=cos(x) вправо на π/2 !
Возврат к преобразованиям функций y=sin(x) и y=cos(x)

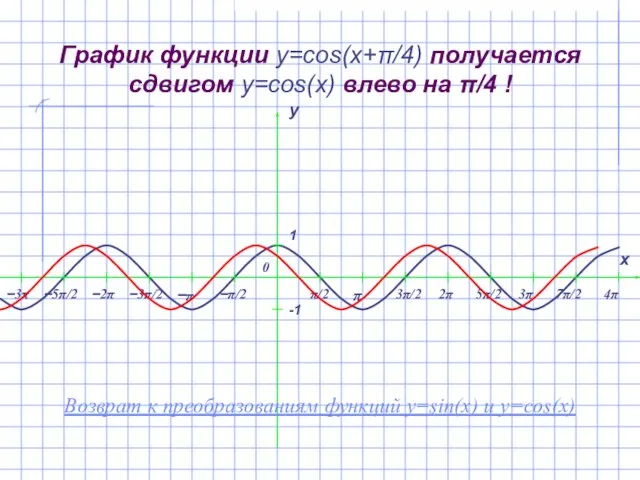
График функции y=cos(x+π/4) получается сдвигом y=cos(x) влево на π/4 !
Возврат к преобразованиям функций y=sin(x) и y=cos(x)

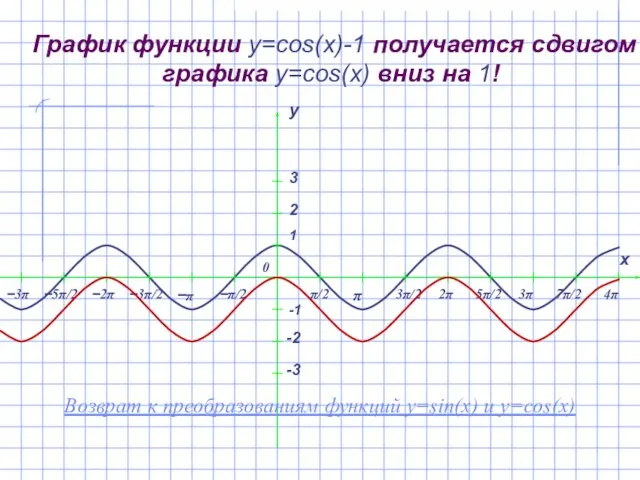
График функции y=cos(x)-1 получается сдвигом графика y=cos(x) вниз на 1!
Возврат к преобразованиям функций y=sin(x) и y=cos(x)

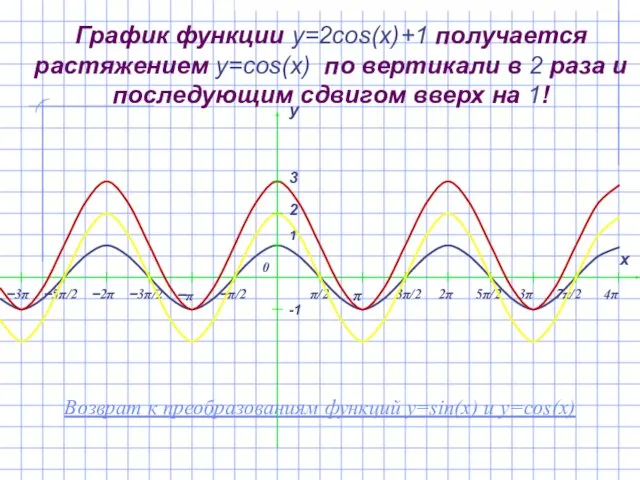
График функции y=2cos(x)+1 получается растяжением y=cos(x) по вертикали в 2 раза и последующим сдвигом вверх на 1!
Возврат к преобразованиям функций y=sin(x) и y=cos(x)