Применение производной к исследованию функций

Понятие «производная» возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики.
Готфрид Вильгельм фон Лейбниц
Иcаак Ньютон
25 декабря 1642 — 20 марта 1727
1 июля 1646 — 14 ноября 1716,

Используя методы дифференциального исчисления английский астроном, математик Эдмон Галлей ещё в XVII веке предсказал возвращение кометы Галлея.
(что, увы, было уже после его смерти). Комета действительно возвратилась, как было предсказано, и позже была названа в его честь.
Комета Галлея вернется во внутреннюю Солнечную систему в следующий раз в 2061 году.
В 1705 году Эдмонд Галлей предсказал, что комета, которую наблюдали в 1531, 1607 и 1682 годах, должна возвратиться в 1758 году

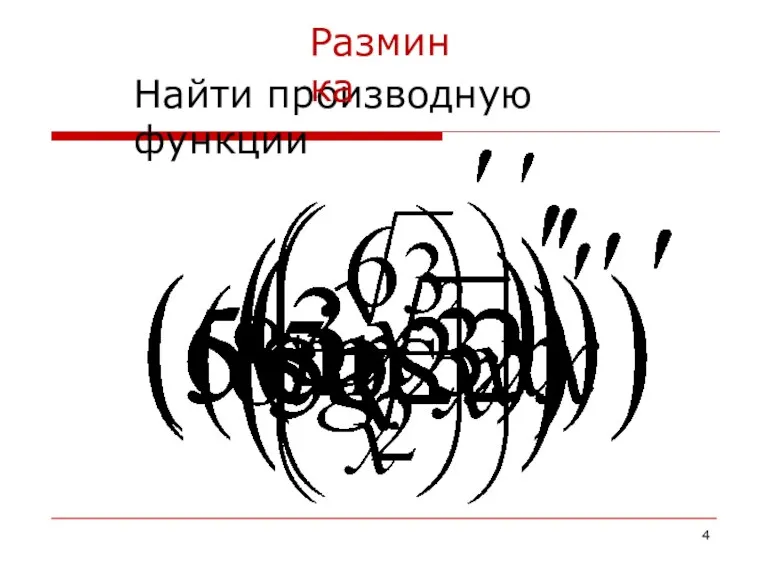
Найти производную функции
Разминка

Признак возрастания и убывания функции
=

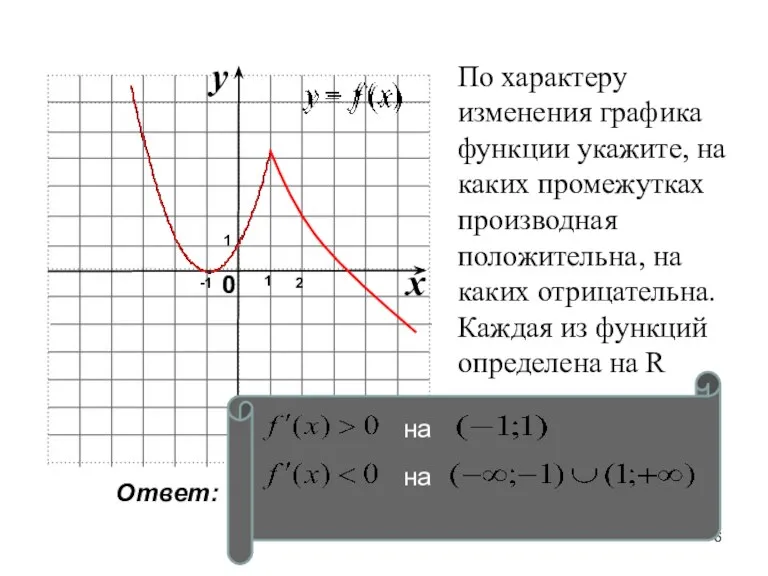
По характеру изменения графика функции укажите, на каких промежутках производная положительна, на каких отрицательна. Каждая из функций определена на R
Ответ:

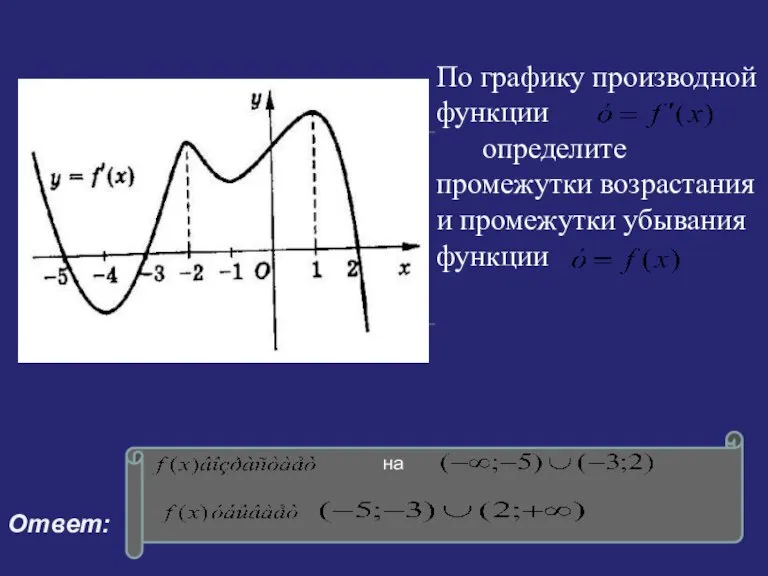
По графику производной функции
определите промежутки возрастания и промежутки убывания функции
Ответ:
1

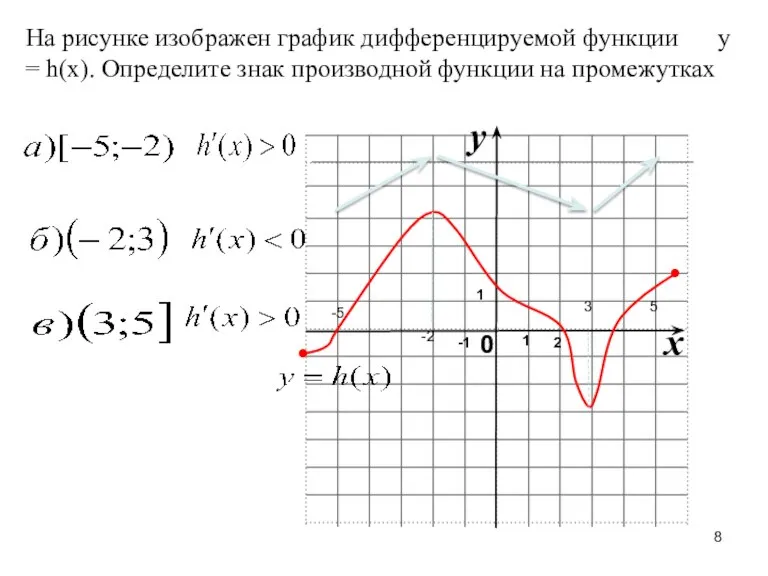
На рисунке изображен график дифференцируемой функции y = h(x). Определите знак производной функции на промежутках
-2
3
-5
5
1

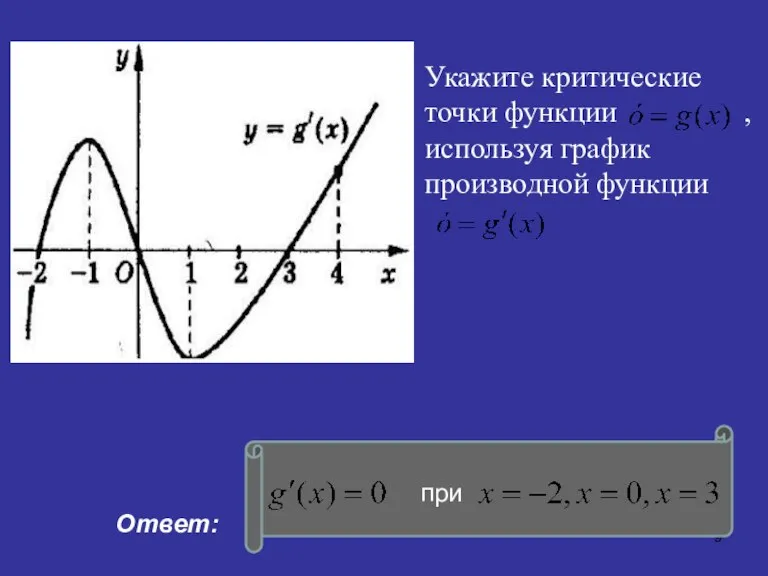
Укажите критические точки функции , используя график производной функции .
Ответ:

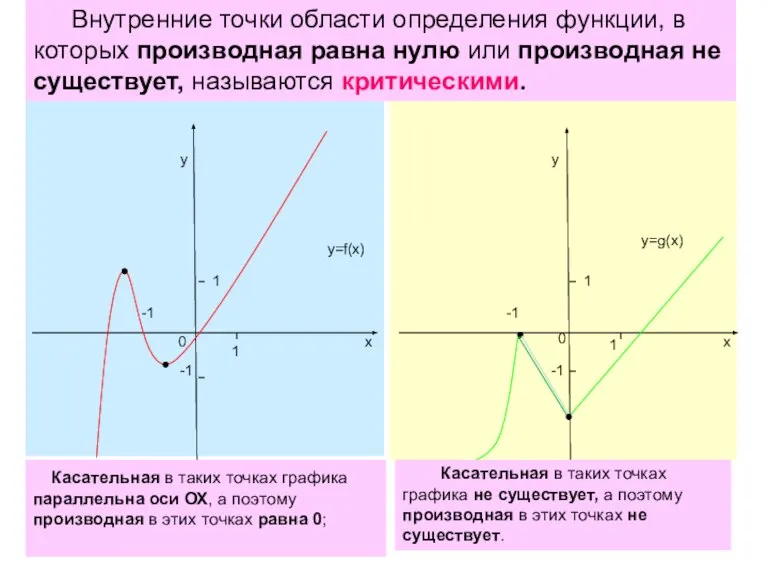
1
1
-1
0
х
у
-1
у
х
1
0
-1
1
-1
y=f(x)
y=g(x)
Касательная в таких точках графика параллельна оси ОХ, а поэтому производная в этих точках равна 0;
Внутренние точки области определения функции, в которых производная равна нулю или производная не существует, называются критическими.
Касательная в таких точках графика не существует, а поэтому производная в этих точках не существует.

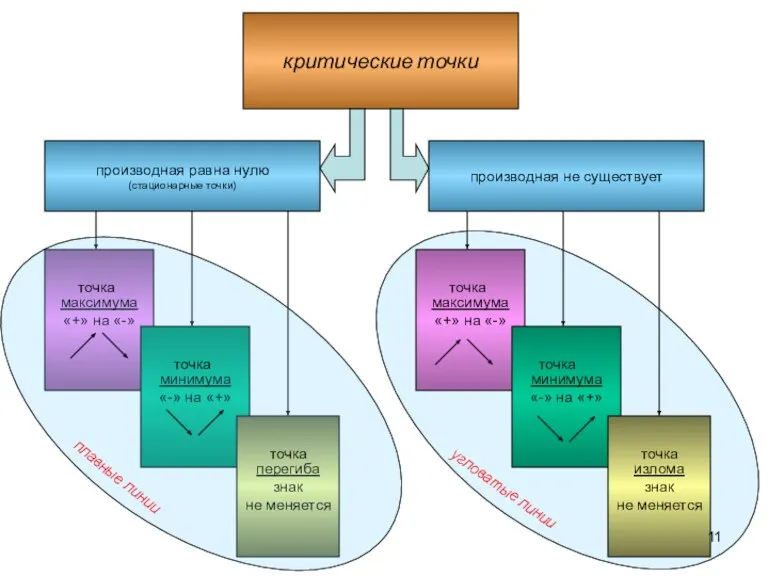
производная равна нулю
(стационарные точки)
критические точки
производная не существует
максимума
«+» на «-»
минимума
«-» на «+»
перегиба
знак
не меняется
максимума
«+» на «-»
минимума
«-» на «+»
излома
знак
не меняется
плавные линии
угловатые линии
точка
точка
точка
точка
точка
точка

Достаточное условие существования экстремума функции:
Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «+» на «-», то х0 – точка максимума функции f(x).
Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «-» на «+», то х0 – точка минимума функции f(x).
3) Если при переходе через критическую точку х0 функции f(x) ее производная не меняет знака, то в точке х0 экстремума нет.

Исследование функций с помощью производной и построение графиков функций.

Схема исследования функции
Найти область определения функции;
Исследовать функцию на четность, нечетность, периодичность;
Найти точки пересечения графика функции с осями координат;
Исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
Найти точки экстремума и экстремальные значения функции;
Построить график функции.

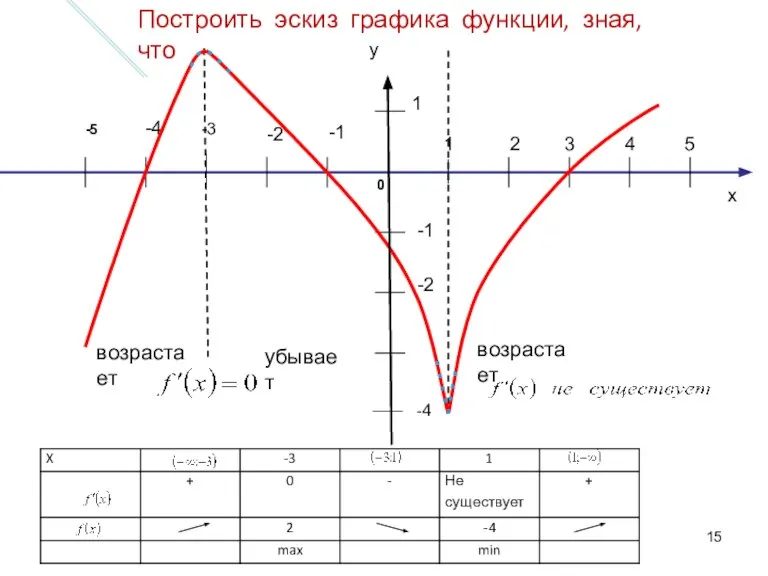
x
1
2
3
4
5
-1
-2
-4
-1
-2
1
-3
-5
0
возрастает
возрастает
убывает
Построить эскиз графика функции, зная, что
y
-4

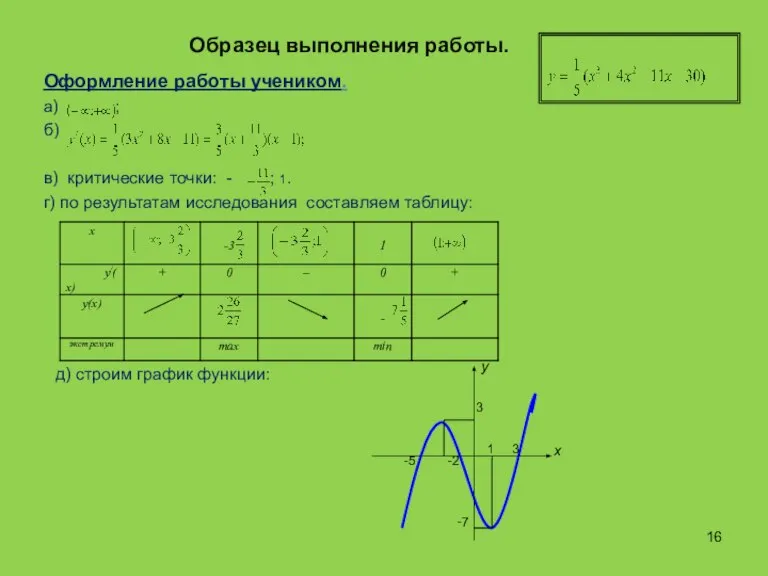
Образец выполнения работы.
Оформление работы учеником.
а) ;
б)
в) критические точки: - ; 1.
г) по результатам исследования составляем таблицу:
д) строим график функции:
1 3
х
у
-5 -2
3
-7

Задачи на нахождение
наибольшего и наименьшего значений