Процентные вычисления в жизненных ситуациях

● Проценты - одно из математических понятий, которые часто встречаются в повседневной жизни. Так, мы часто читаем или слышим, что, например, в выборах приняли участие 52,5% избирателей, промышленное производство сократилось на 11,3%, банк начисляет 12% годовых, молоко содержит 3,2% жира и т.д.
● Слово «процент» происходит от латинского слова procentum,что означает «за сотню» или «со ста».
Историческая справка

● Уже в в клинописных табличках вавилонян содержатся задачи на расчёт процентов. Проценты были известны в Индии, в Древнем Риме. От римлян проценты перешли к другим народам.
● В средние века в Европе в связи с развитием торговли приходилось рассчитывать не только проценты, но и проценты с процентов ,то есть сложные проценты, как называют их в наше время. Отдельные конторы при вычислениях процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы.

Впервые опубликовал такие таблицы в 1584 году Симон Стевин - инженер из Нидерландов.

● Знак «%» происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчётах часто писалось сокращённо cto . Отсюда путём дальнейшего упрощения в скорописи буквы t в наклонную черту произошёл современный символ для обозначения процента.
● Существует и другая версия возникновения этого знака. В 1685 году в Париже была опубликована книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал % .

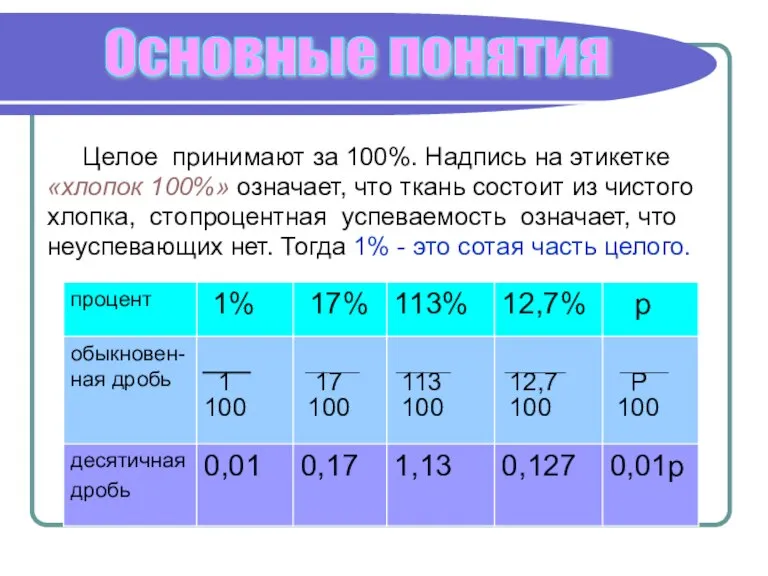
Целое принимают за 100%. Надпись на этикетке
«хлопок 100%» означает, что ткань состоит из чистого
хлопка, стопроцентная успеваемость означает, что
неуспевающих нет. Тогда 1% - это сотая часть целого.
ж
Основные понятия

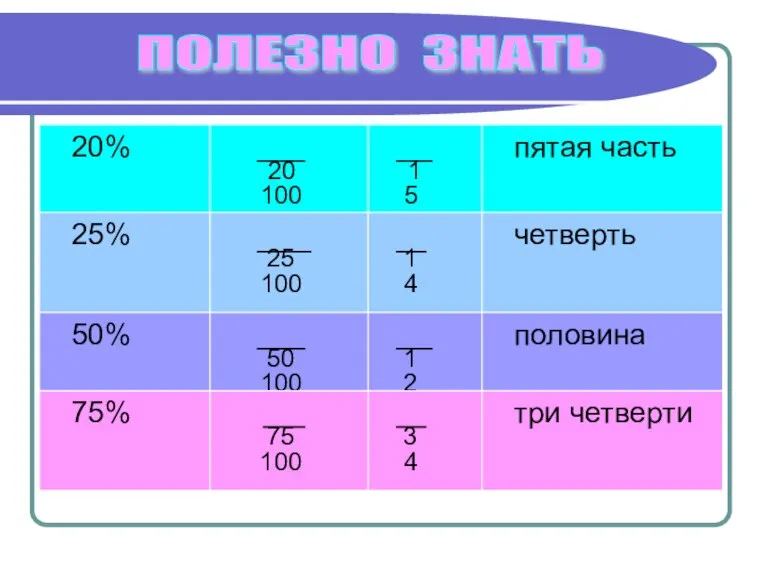
ПОЛЕЗНО ЗНАТЬ

Тема 1.
Чтобы найти процент от заданного числа, нужно это число умножить на проценты.
Задана величина S , тогда p% от S можно найти так:
S · p% = S ∙ p/100
или
S · p% = S ∙ 0,01p=0,01pS
Вычисление количеств по процентам

Н А П Р И М Е Р
Задача. Товар стоил 500 руб. Его цена повысилась на 20%. На сколько руб. повысилась цена?
Решение.
Найдём 20% от 500 руб.
500 · 20% = 500 · 20/100 = 100
или
500∙ 20% = 500 · 0,2 = 100
Ответ: 100 рублей.

Чтобы найти число, p% которого известны, нужно известное число разделить на проценты.
Тогда число, p% которого равны A, можно найти так:
A : p
A : p% = 100
A : 0,01p

Н А П Р И М Е Р
Задача. При помоле пшеницы получается 80% муки. Сколько пшеницы нужно смолоть, чтобы получить 480 кг муки?
Решение.
Найдём число, 80% которого есть 480 кг
480 : 80% = 480 : 0,8 = 4800 : 8 = 600
Ответ: 600 кг .

● Найдём количество, большее(меньшее), чем A, на p%.
● Количество A принимаем за 100% . Если новое количество больше (меньше), чем A на p%, то оно составляет (100±p)% от А.
А ∙ (100 ± p)% = А . 100 ± p = A ( 1 ± p )
100 100
А · (100 ± p)% = A (1 ± 0,01p)

Н А П Р И М Е Р
Задача 1. Зарплата рабочего 6000 руб. Сколько будет получать рабочий после повышения зарплаты на 12%?
Решение.
6000 · (100+12)% = 6000 ∙ 112% =6000 · 1,12 = 6720
Ответ: 6720 рублей.
Задача 2. Товар в 200 руб. подешевел на 10%. Какова новая цена товара?
Решение.
200 · (100-10)% = 200 ∙ 90% = 200 · 0,9 = 180
Ответ: 180 рублей.

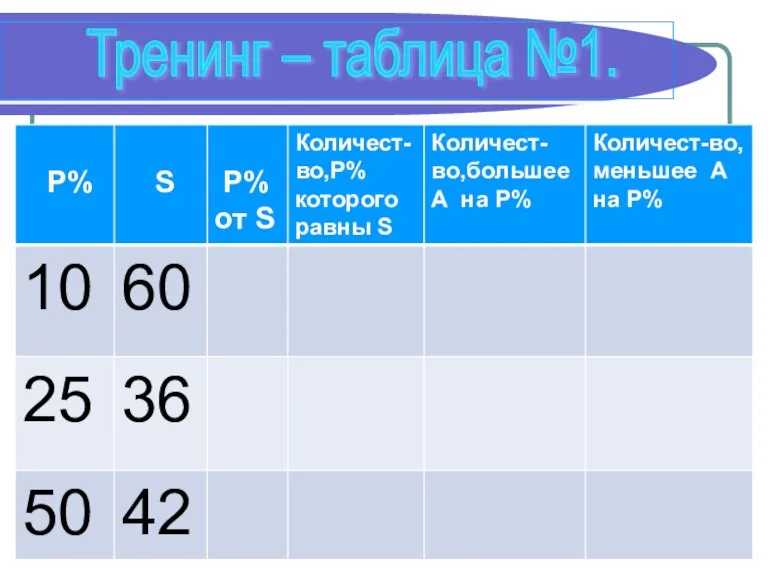
Тренинг – таблица №1.

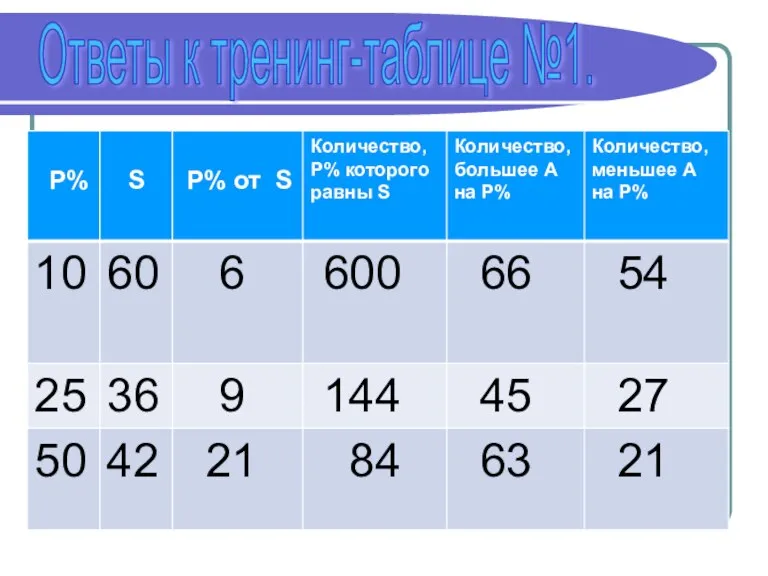
Ответы к тренинг-таблице №1.

Тема 2. Вычисление процентов по количествам.
Сколько процентов составляет А от В можно найти по формуле:
А / В * 100%.
Задача. Сколько процентов составляет 150 от 600?
Решение: 150 / 600 * 100% = 25%
Ответ: 25%.

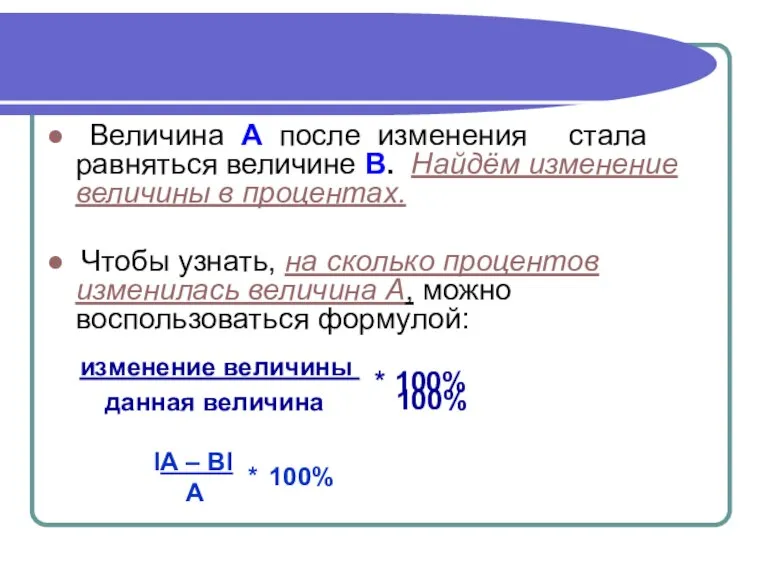
● Величина А после изменения стала равняться величине В. Найдём изменение величины в процентах.
● Чтобы узнать, на сколько процентов изменилась величина А, можно воспользоваться формулой:
изменение величины * 100%
данная величина 100%
IА – ВI * 100%
А

Задача 1. Товар стоимостью 150 р. Уценён до 120 р. На сколько процентов уценили товар ?
Решение: 150-120 * 100%= 30 * 100%=20%
150 150
Ответ: на 20%.
Задача 2. На сколько процентов
а) 50 больше 40; б) 40 меньше 50?
Решение: а) Было число 40, стало 50.
50- 40 * 100% = 1 / 4 * 100% = 25 %
40
б) Было число 50, стало 40.
50- 40 * 100% = 1 / 5 * 100% = 20%
50
Ответ: на 25%, на 20%.
Н А П Р И М Е Р

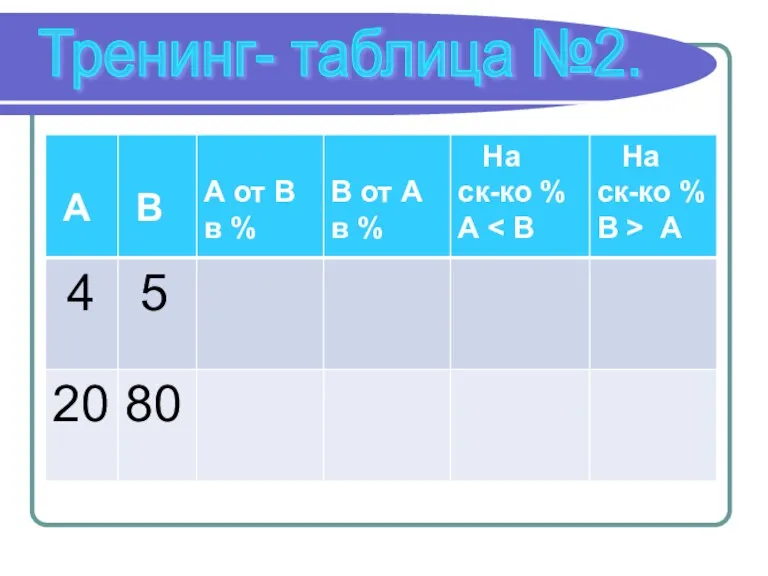
Тренинг- таблица №2.

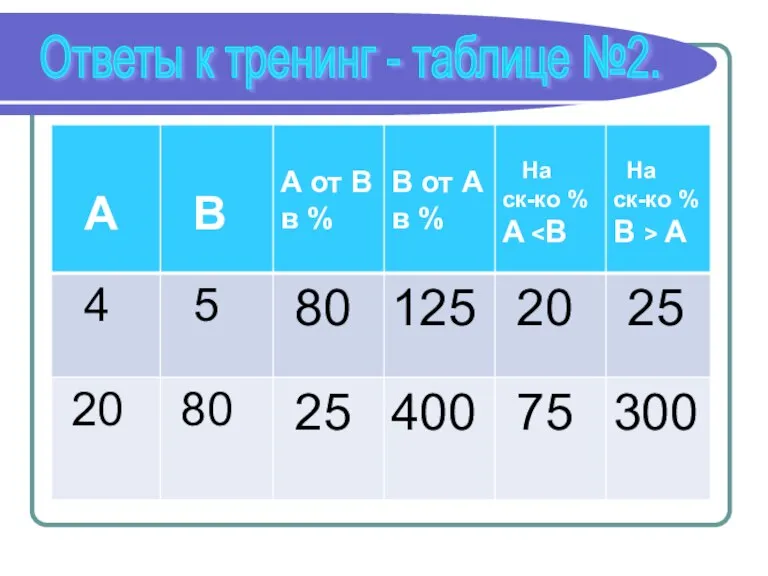
Ответы к тренинг - таблице №2.

Тема 3. ЗАДАЧИ С ФИНАНСОВО – ЭКОНОМИЧЕСКИМ СОДЕРЖАНИЕМ
s0-начальное значение величины sn-значение, полученное в результате некоторых изменений начальной величины.
n-количество изменений
p-процент изменения
При решении задач на повышение (снижение) цены товара на p1%, затем на p2% и т.д. используют формулу:
sn= s0(1± 0,01p1)·(1± 0,01p2)·…∙(1± 0,01pn)
или
sn= s0(1± p1/100)·(1± p2/100)·…∙(1± pn/100)

Если повышение (снижение) происходит несколько раз на один и тот же процент, то используют формулу:
Sn = S0(1± 0,01p)n или
Sn = S0(1± p/100)n
Эти формулы называются формулами сложных процентов. Их так же используют при решении задач о начислении процентов по вкладам.

ЗАДАЧА 1. Летом фрукты стоили 30руб. В осенне - зимний период цена возрастала трижды: на 10%, на20%, на 25%. Какова зимняя цена на фрукты ?
Решение. S=30(1+10/100)(1+20/100)(1+25/100)=49,5
Ответ: 49 руб. 50 коп.
ЗАДАЧА 2. Вкладчик открыл счёт в банке, внеся 2000руб. на вклад, годовой доход по которому составляет 12%. Какая сумма будет лежать на его счёте через 6 лет?
Решение. S=2000(1+12/100)6=2000+(1,12)6=3947,65
Ответ: 3947 руб. 65 коп.
н а п р и м е р

Решите задачу №1
Б А Н К
Банк «Винни-Пух и Пятачок» начисляет своим вкладчикам по 10% ежемесячно. Иа сделал вклад в этот банк в размере 1,00$. Сколько денег он может снять со своего счета через два месяца?

Используем формулу сложных процентов Sn=S0(1 + P/100)n
S2= 1,00∙( 1+ 10/100)2=1·(1,1)2=1,21 Ответ: 1,21 $.
Проверьте своё решение

Решите задачу №2
Клиент банка имеет счет, по которому начисляется 10% годовых. Через сколько лет он сможет купить автомобиль по цене 177 000 рублей, если на счете у него
100000 рублей?

Используем формулу сложных процентов:
Sn=S0(1 + P/100)n
Проверьте своё решение
S0=100 000 Sn=177 000
получаем уравнение с одним неизвестным
177 000 = 100 000(1+10/100)n
177 000 = 100 000 ∙ 1,1n
1,1n = 1,77
n = 6, т.к. 1,16 = 1,771561.
Ответ : 6 лет.