Issledovanie-funkciy-i-postroenie-grafikov.ppt
Содержание
- 1. Issledovanie-funkciy-i-postroenie-grafikov.ppt
- 2. Тема урока: Исследование функций и построение графиков
- 3. Цель урока:Цель урока: Совершенствовать умение применять
- 4. Алгоритм исследования Алгоритм исследования функцийфункций 1) Найти
- 5. Область определения функции - множество значений,
- 6. Функция f возрастает на множестве Р, если
- 7. Тока х 0 называется точкой минимума функции
- 9. Проведите по общей схеме исследование функции 1
- 10. Вариант 1
- 11. Постройте график функции Постройте график функции ff
- 12. 1 2 3 4 5
- 13. Итог урокаИтог урока 5 плюсов – оценка «5» 4 плюса- оценка «4» 3 плюса –оценка «3»
- 14. Домашнее заданиеДомашнее задание Задание- практическое:
- 15. З адание аналитическое: Отыщите функцию, среди
- 16. Поделитесь своим впечатлениемПоделитесь своим впечатлением 1)Что вы
- 17. Спасибо за урок!
- 18. Список литературы:Список литературы: 1. Учебник А.Н. Колмогоров
- 19. Скачать презентацию
- 20. Похожие презентации
Тема урока: Исследование функций и построение графиков
![Вариант 1 Вариант 2 1. D ( y )=[-8;5], E ( y )=[-2;5]](/files/22/21718/page-10.jpg "Вариант 1 Вариант 2 1. D ( y )=[-8;5], E ( y )=[-2;5]")
Слайды презентации
Слайд 1
Павленко Надежда Васильевна
учитель математики и физики
НОУ «СОШ с углубленным изучением
отдельных предметов имени В.Д. Чурсина»
Слайд 2
Тема урока: Исследование
функций и построение графиков
Слайд 3
Цель урока:Цель урока:
Совершенствовать умение применять полученные
сведения для
построения графиков функций на основе предварительного исследования
Слайд 4
Алгоритм исследования Алгоритм исследования
функцийфункций
1) Найти области определения и значений
данной функции f . 2) Найти координаты точек пересечения
графика с осями координат. 3) Найти промежутки знакопостоянства функции f
. 4) Выяснит, на каких промежутках функция f возрастает, а на каких убывает. 5) Найти точки экстремума, вид экстремума (максимум или минимум) и вычислить значения f в этих точках.
Слайд 5
Область определения функции -
множество значений, принимаемых независимой
переменной
х . Область значения функции - множество значений функции f(x)
Слайд 6
Функция f возрастает на множестве Р, если для
любых х
1
и х 2 из множества Р, таких, что х 2 >х 1,
выполнено неравенство f (х) 2 > f (х 1 ). Функция
f убывает на множестве Р, если для любых х 1 и х 2 из множества Р, таких, что х 2 >х 1, выполнено неравенство f (х) 2 < f (х 1 ).
Слайд 7
Тока х
0 называется точкой минимума функции f ,
если для
всех з из некоторой окрестности х 0 выполнено неравенство f
(х)> f (х 0 ). Тока х 0 называется точкой максимума функции
f , если для всех з из некоторой окрестности х 0 выполнено неравенство f (х)< f (х 0 ).
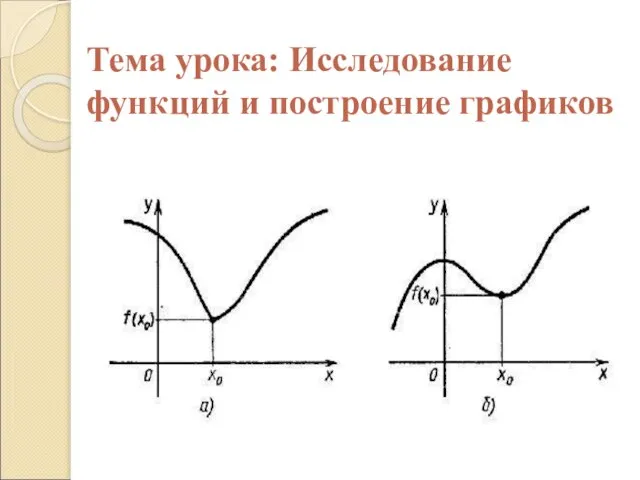
Слайд 9
Проведите по общей схеме
исследование функции
1 Вариант –рис.57 график а)
2
Вариант- рис. 57 график б)
Слайд 10
Вариант 1
Вариант 2 1. D ( y )=[-8;5], E
( y )=[-2;5] 1. D ( y )=[-6;6], E ( y )=[-2;2] 2. c Ox (1;0), (5;0) 2. c Ox (-4;0), (0;0), (4;0) c Oy (2;0) с Оу (0;0) 3. f ( x )>0 (-8;0), (0;1) 3. f ( x )>0 (-4;0), (4;6) f ( x )<0 (1;5) f(x)<0 (-6;-4), (0;4) 4. возрастает (-5;-1), (3;5) 4. возрастает(-6;-2), (2;6) убывает (-8;5), (-1;3) убывает (-2;2) 5. максимум f (-1)=5 5. максимум f (-2)=2 минимум f (-5)=1, f (3)=-2 минимум f (2)=2
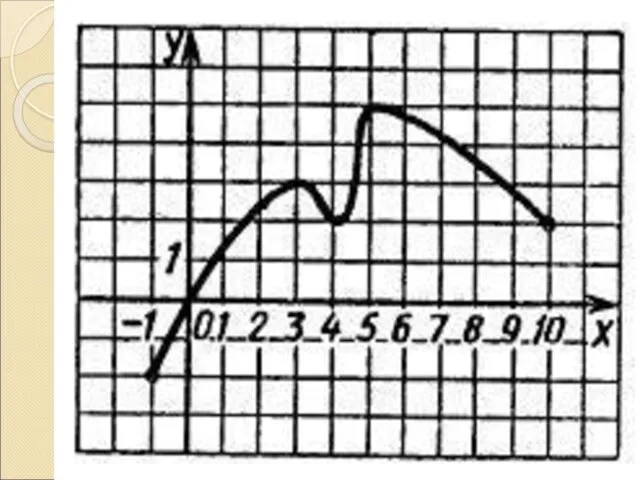
Слайд 11
Постройте график функции Постройте график функции
ff
, если , если
известны ее свойстваизвестны ее свойства Свойство функции 1 Область определения Область значений
[-6;6] [-2;5] 2 Точки пересечения графика: а) с осью Ох б) с осью Оу
А(-4;0). В(-2;0) С(0;2,5) 3 Промежутки знакопостоянства: а) f ( x )>0 б) f(x)<0 [-6;-4). (-2;6] (-4;-2) 4 Промежутки : а) возрастания б) убывания [-3;1], [4;6] [-6;-3], [1;4] 5 Точки максимума, максимум функции Точки минимума, минимум функции (1)=3 (-3)=-2; (4)=1 6 Дополнительные точки графика f(-6)=3; f(6)=5
Слайд 12
1
2
3
4
5
Слайд 13
Итог урокаИтог урока
5 плюсов – оценка «5»
4 плюса- оценка
«4» 3 плюса –оценка «3»
Слайд 14
Домашнее заданиеДомашнее задание
Задание- практическое:
пункт 6 читать; №94 (б, г); №95
(в, г); № 96 (б);
№97 (в)
Слайд 15
З адание аналитическое:
Отыщите функцию, среди предложенных, исходя
из её «автобиографии»: Я – функция сложная, это известно,
Ещё расскажу, если Вам интересно, Что точку разрыва и корень
имею, И есть интервал, где расти не посмею. Во всём остальном положительна, право. И это конечно не ради забавы. Для чисел больших я стремлюсь к единице. Найдите меня среди прочих в таблице.
Слайд 16
Поделитесь своим впечатлениемПоделитесь своим впечатлением
1)Что вы сегодня изучали на уроке?
2)
Какие задания вызвали у вас затруднения? 3) Какие задания вам
понравились? 4)Какие знания математики пригодились вам на уроке?
Слайд 17
Спасибо за урок!
Слайд 18
Список литературы:Список литературы:
1. Учебник А.Н. Колмогоров «Алгебра и начала анализа.
10-11 класс». 2. Денищева Л.О. Седова Е.А. Дидактические материалы по
алгебре и началам анализа 10-11 класс. 3. Кузнецова Г.М. Программа для
общеобразовательных школ, гимназий. Математика., 2000. 4. Ивлев Б.М. Дидактические материалы по алгебре и началам анализа 10 класс. М.
Чтобы скачать презентацию - поделитесь ей с друзьями с помощью
социальных кнопок.
