Содержание
- 2. Что называют разложением многочлена на множители? a2 – 5ab = a2 – 25 = a2 –
- 3. 8 – a3 = x3 + 64 = a3 – 25а = а(а + 4b) a2
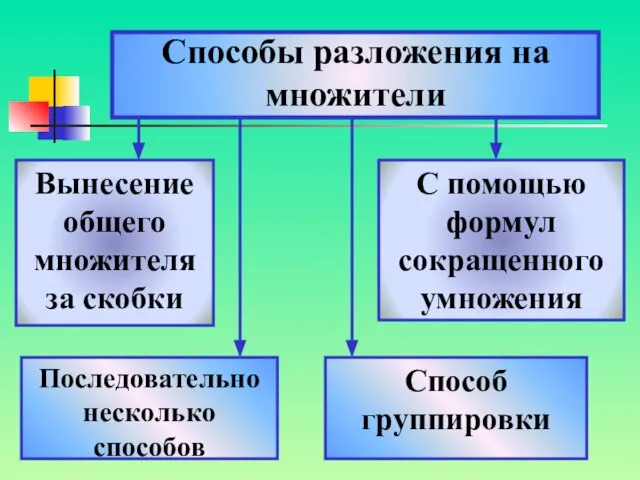
- 4. Способы разложения на множители Вынесение общего множителя за скобки Способ группировки С помощью формул сокращенного умножения
- 5. Решите уравнения (х – 2)(х + 2) = 0 Х= 2 и х = - 2
- 6. х2 – 16 = 0 (х – 4)(х + 4) = 0 х = 4 и
- 7. х2 + 10х + 25 =0 (х + 5)2 = 0 х = - 5 Ответ:
- 8. 9х – х3 = 0 х(9-х2) = 0 х(3 – х)(3 + х) = 0 х
- 9. Разложение на множители позволило нам сократить дробь. Найдите значение числового выражения 532-472 612-392 Самое эффективное решение
- 10. Алгоритм отыскания общего множителя нескольких одночленов 1. Найти наибольший общий делитель коэффициентов всех одночленов, входящих в
- 11. Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из
- 12. Разложить на множители: -x4y3-2x3y2+5x2. Воспользуемся сформулированным алгоритмом. Наибольший общий делитель коэффициентов –1, -2 и 5 равен
- 13. Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки. Вывод: за
- 14. Способ группировки Рассмотрим пример: разложите на множители многочлен х3+х2у– 4у – 4х = (х2+х2у) – (4х+4у)
- 15. bx2 + 2b2 – b3 – 2x2 = (bx2 – b3) – (2x2–2b2)= = b(x2 –
- 16. Разложение многочлена на множители с помощью формул сокращенного умножения Вспомните эти формулы: a2-b2=(a-b)(a+b); a3-b3=(a-b)(a2+ab+b2); a3+b3=(a+b)(a2-ab+b2); a2+2ab+b2=(a+b)2;
- 17. Первую из этих формул можно применять к выражению, представляющему собой разность квадратов (безразлично чего – чисел,
- 18. Воспользовались формулой суммы кубов. а6 + 27b3 = (a2)3 + (3b)3 = = (a2 + 3b)(a4
- 19. Х 2 4 0,8ху + 0,16у 2 Х 2 2 = 2 · 1 2 х
- 20. Воспользовались формулой разности квадратов. х6 – 4а4 = = (х3)2 – (2а2)2 = (х3 – 2а2)
- 21. Разложение многочлена на множители с помощью комбинации различных приемов В математике не так часто бывает, чтобы
- 22. Сначала займемся вынесением общего множителя за скобки. Рассмотрим коэффициенты 36, 96, 64. Все они делятся на
- 23. Итак, за скобки вынесем 4a2b3. Тогда получим: 36a6b3-96a4b4+64a2b5 = 4a2b3(9a4-24a2b+16b2) 2) Рассмотрим трехчлен в скобках: 9a4-24a2b+16b2.
- 24. Все условия полного квадрата соблюдены, следовательно, 9a4-24a2b+16b2= 3) Комбинируя два приема (вынесение общего множителя за скобки
- 25. 2. Разложить на множители x4+x2a2+a4 Применим метод выделения полного квадрата. Для этого представим x2a2 в виде
- 26. 3. Разложить на множители n3+3n2+2n Сначала воспользуемся тем, что n можно вынести за скобки: n(n2+3n+2). Теперь
- 27. Окончательно получаем: n2+3n+2= n2+2n+n+2 = = (n2+2n)+(n+2) = n(n+2)+(n+2) = = (n+2)(n+1). n(n+1)(n+2). n2+3n+2=
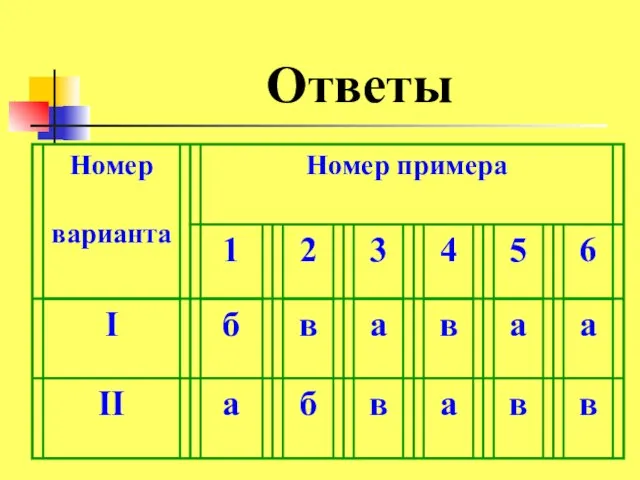
- 29. Ответы
- 30. До новых встреч!
- 32. Скачать презентацию



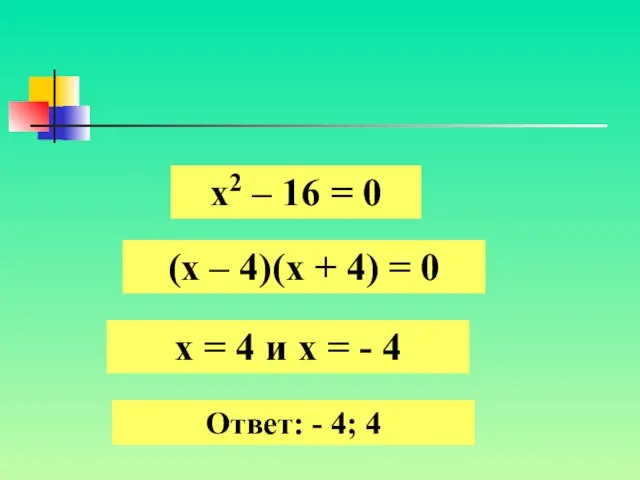
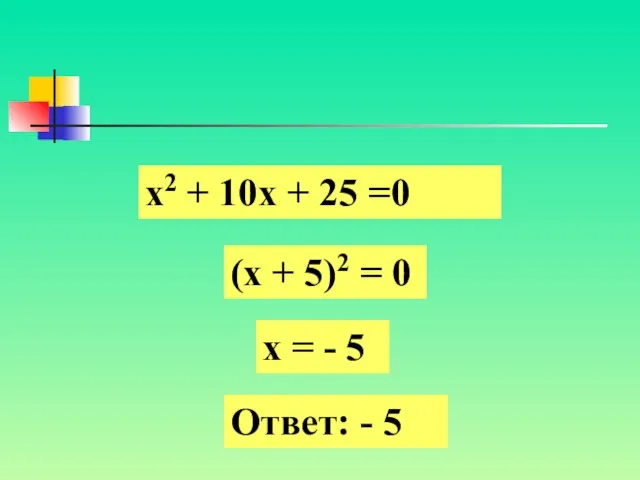
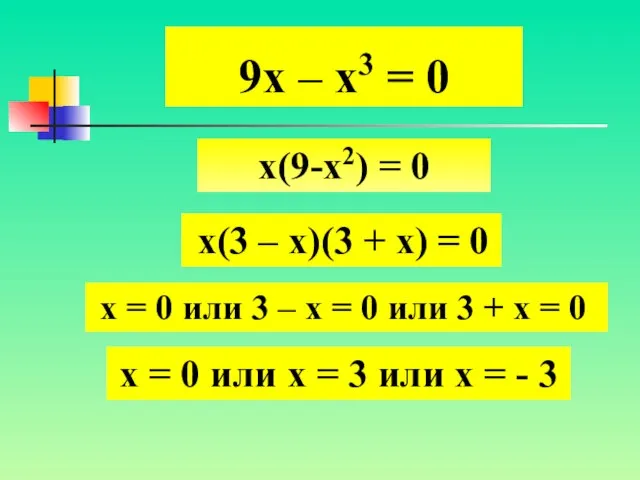





















 Виды показательных уравнений
Виды показательных уравнений  Путешествие в страну дробных чисел
Путешествие в страну дробных чисел Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Старая сказка на новый лад
Старая сказка на новый лад ТОЖДЕСТВА 7 класс
ТОЖДЕСТВА 7 класс  Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_
Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_ 9-klass-kvadratichnaya-funkciya.ppt
9-klass-kvadratichnaya-funkciya.ppt Метод рационализации
Метод рационализации Графическое решение систем уравнений
Графическое решение систем уравнений Презентация на тему Аварии на радиационно-опасных объектах
Презентация на тему Аварии на радиационно-опасных объектах  Сложение и вычитание смешанных чисел 5 класс
Сложение и вычитание смешанных чисел 5 класс Всё о квадратном уравнении
Всё о квадратном уравнении Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766
Презентация на тему ИСТОРИЧЕСКИЙ ПОРТРЕТ НИКОЛАЯ МИХАЙЛОВИЧА КАРАМЗИНА (1766 Квадратный трехчлен и его приложения
Квадратный трехчлен и его приложения Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Алгебра модуля
Алгебра модуля Построение арифметических выражений
Построение арифметических выражений Uravneniya-s-parametrami.ppt
Uravneniya-s-parametrami.ppt Обратные тригонометрические функции
Обратные тригонометрические функции vzaimno-obratnye-funkcii.ppt
vzaimno-obratnye-funkcii.ppt Комбинаторные задачи Перестановки РазмещенияСочетания (выборки)
Комбинаторные задачи Перестановки РазмещенияСочетания (выборки) Арифметическая прогрессия.Формула n –го члена арифметической прогрессии
Арифметическая прогрессия.Формула n –го члена арифметической прогрессии Как появилось книгопечатание на Руси
Как появилось книгопечатание на Руси Свойства функций
Свойства функций Одночлены и многочлены 7 класс
Одночлены и многочлены 7 класс Презентация на тему Экзамен без стресса
Презентация на тему Экзамен без стресса  Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений