Содержание
- 2. ЗАДАЧИ Задача №1. Задача №2. Задача №8. Задача №9. Задача №4. Задача №5. Задача №10. Задача
- 3. ЗАДАЧА №1
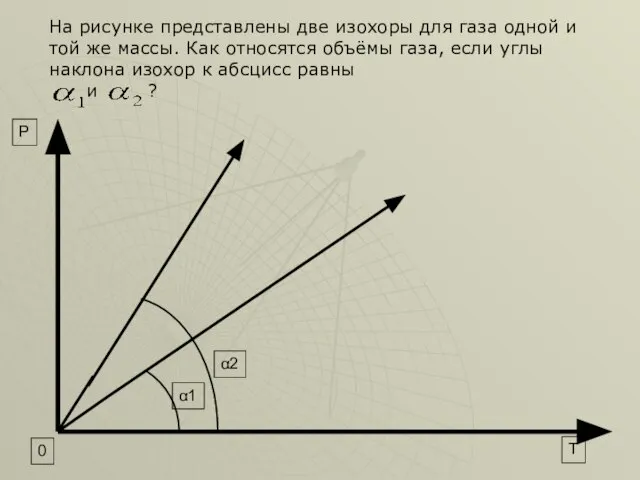
- 4. α2 α1 0 T P На рисунке представлены две изохоры для газа одной и той же
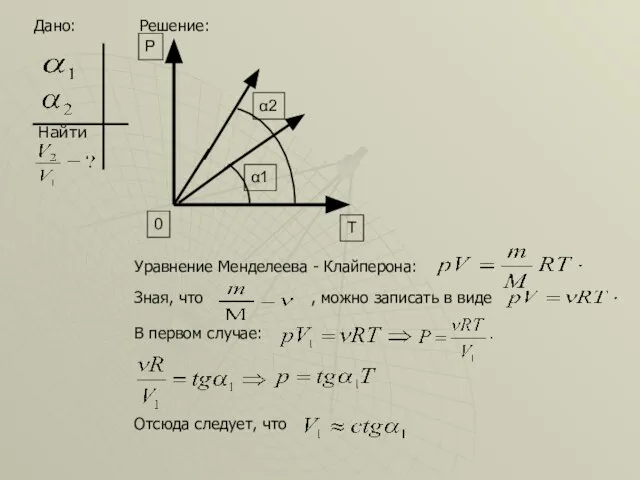
- 5. Найти: Дано: Решение: Уравнение Менделеева - Клайперона: Зная, что , можно записать в виде В первом
- 6. Во втором случае: Исходя из выше написанного следует, что Ответ:
- 7. ЗАДАЧА №2
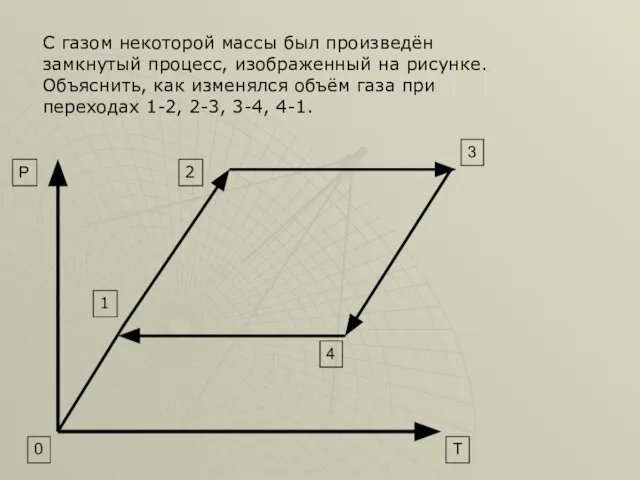
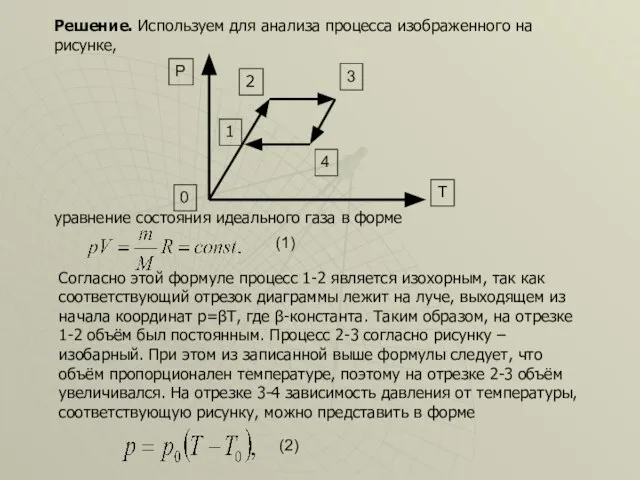
- 8. С газом некоторой массы был произведён замкнутый процесс, изображенный на рисунке. Объяснить, как изменялся объём газа
- 9. 3 4 0 T P 2 1 Решение. Используем для анализа процесса изображенного на рисунке, уравнение
- 10. откуда следует, что на отрезке 3-4 объём увеличился из-за уменьшения температуры.Отрезок 4-1 – вновь изобара. Следовательно,
- 11. Ответ.1-2-оставался постоянным; 2-3-увеличивался пропорционально Т; 3-4-увеличивался; 4-1-уменьшался пропорционально Т.
- 12. ЗАДАЧА №3
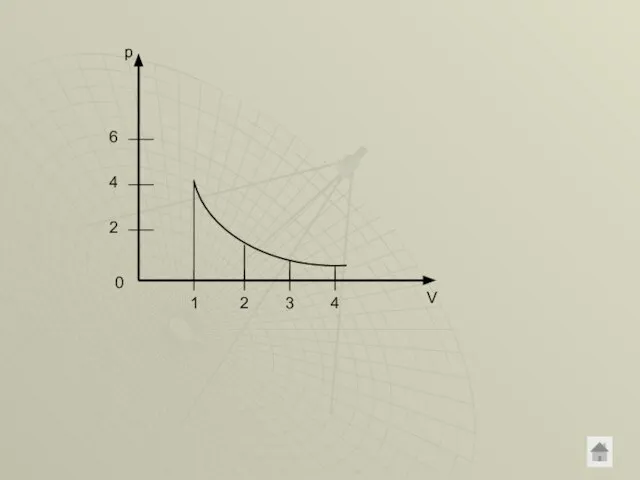
- 13. Начертить изотерму процесса для случая pV=40. Пользуясь графиком ответить на вопрос: на сколько изменился объем данной
- 14. p V 1 2 3 4 2 4 6 0
- 15. ЗАДАЧА №4
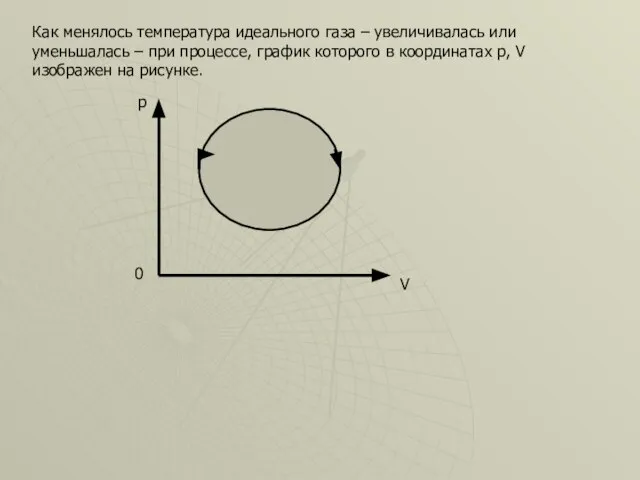
- 16. Как менялось температура идеального газа – увеличивалась или уменьшалась – при процессе, график которого в координатах
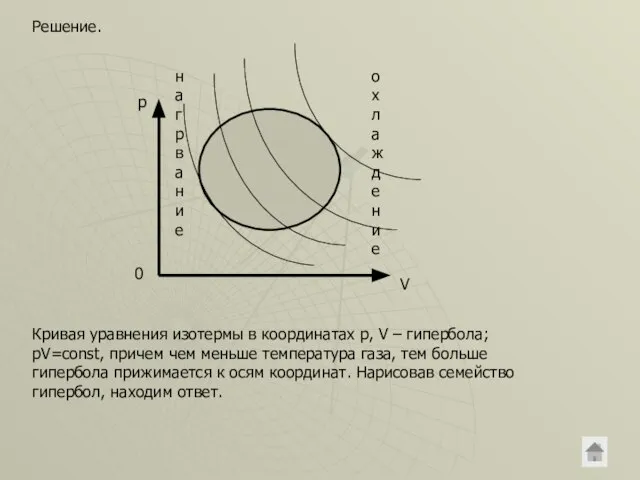
- 17. Решение. p V 0 нагрвание охлаждение Кривая уравнения изотермы в координатах p, V – гипербола; pV=const,
- 18. ЗАДАЧА №5
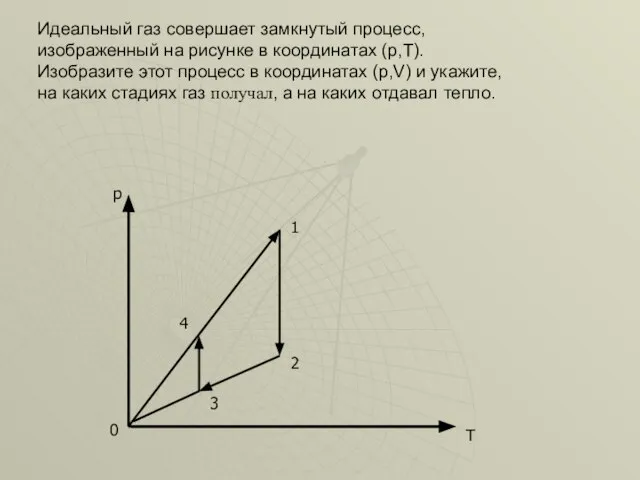
- 19. Идеальный газ совершает замкнутый процесс, изображенный на рисунке в координатах (p,T).Изобразите этот процесс в координатах (p,V)
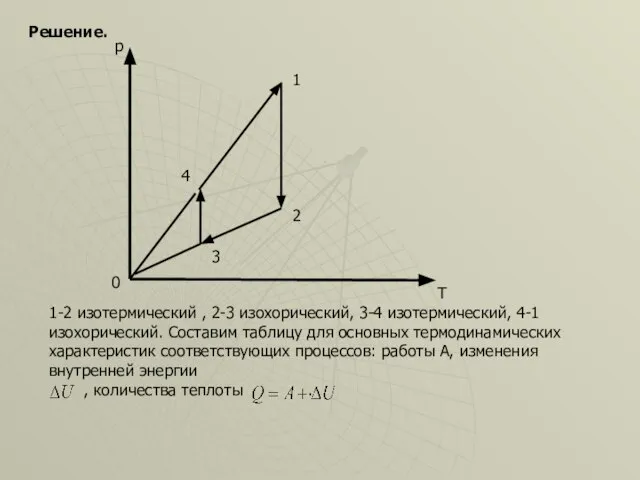
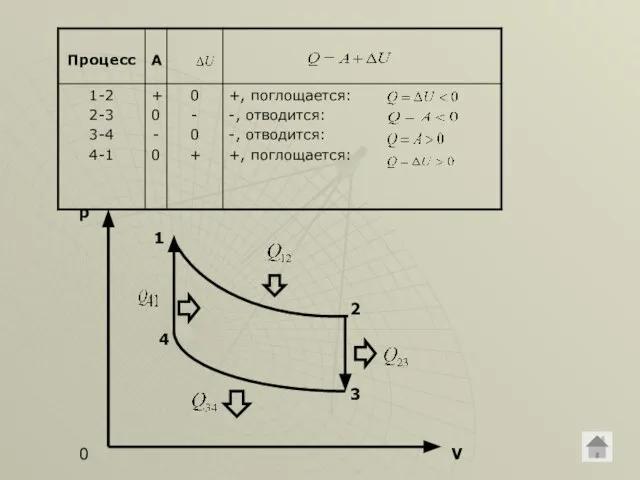
- 20. 0 р 1 2 3 4 Решение. Т 1-2 изотермический , 2-3 изохорический, 3-4 изотермический, 4-1
- 21. p V 0 1 2 3 4
- 22. ЗАДАЧА №6
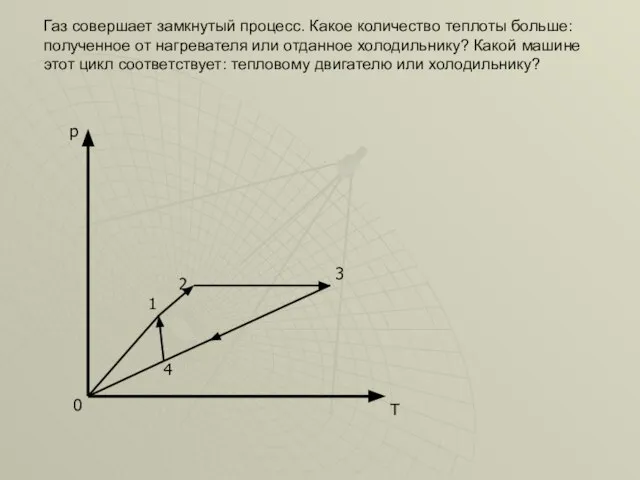
- 23. Т р 0 1 2 4 3 Газ совершает замкнутый процесс. Какое количество теплоты больше: полученное
- 24. Cформулируем общий алгоритм решения этой задачи: перевести цикл в координаты (p, V) и составить таблицу; установить
- 25. Решение: 0 p V 4 1 2 3 В координатах (p,V) цикл обходится по часовой стрелке,
- 26. При контакте с нагревателем система получает тепло а тепло отдает холодильнику. Если цикл запустить в обратном
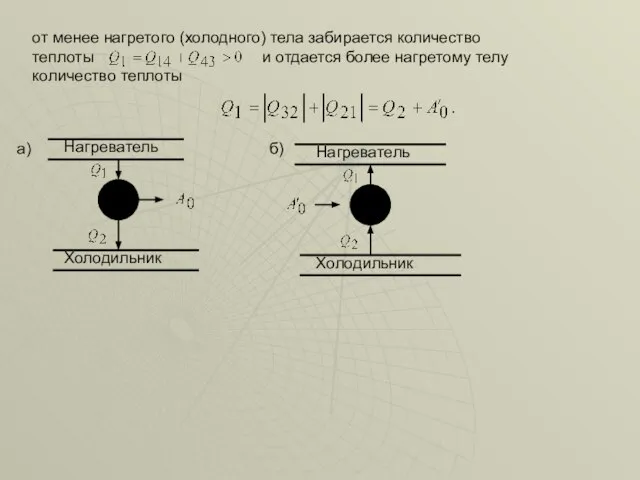
- 27. от менее нагретого (холодного) тела забирается количество теплоты и отдается более нагретому телу количество теплоты Нагреватель
- 28. а) если цикл соответствует тепловому двигателю (обход по часовой стрелке), КПД равен: (1) б) если цикл
- 29. где - температура более нагретого тела, - температура холодного тела, от которого отбирается тепло; г) если
- 30. ЗАДАЧА №7
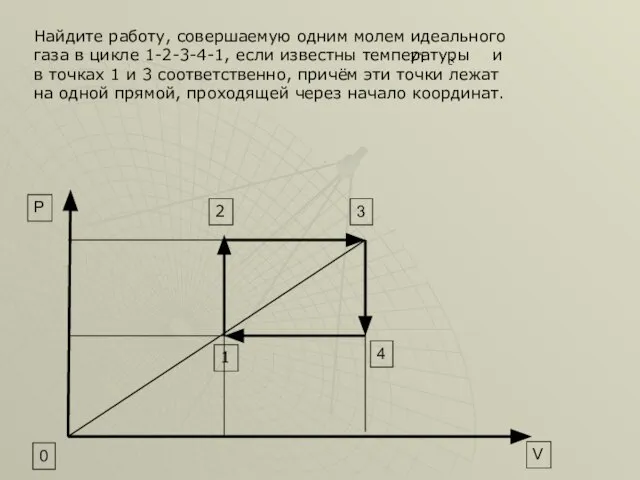
- 31. Найдите работу, совершаемую одним молем идеального газа в цикле 1-2-3-4-1, если известны температуры и в точках
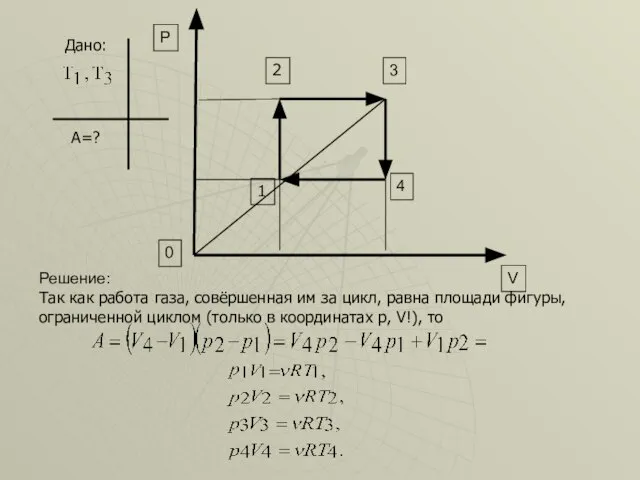
- 32. Дано: А=? 3 4 0 V P 2 1 Так как работа газа, совёршенная им за
- 33. В системе уравнений: (1) (2) (3) (4) Уменьшаем индексы: Из этого равенства, а также из второго
- 34. Так как точки 1 и 3 лежат на прямой, проходящей через начало координат, то или после
- 35. Ответ.
- 36. ЗАДАЧА №8
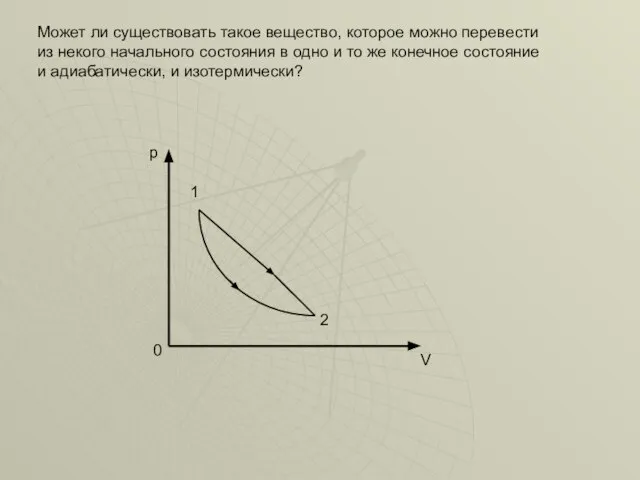
- 37. Может ли существовать такое вещество, которое можно перевести из некого начального состояния в одно и то
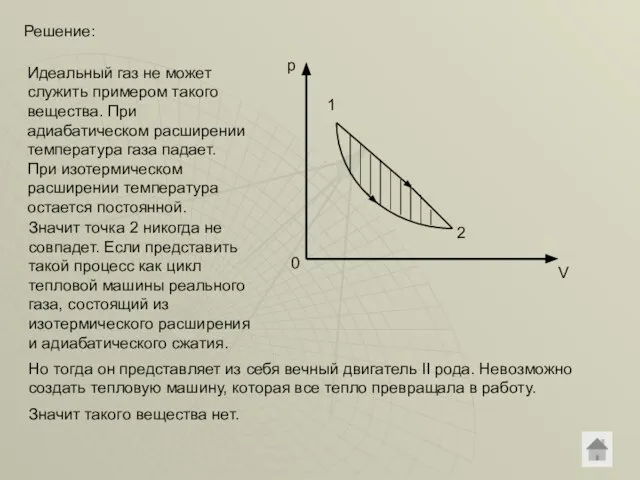
- 38. Решение: 0 p V 1 2 Идеальный газ не может служить примером такого вещества. При адиабатическом
- 39. ЗАДАЧА №9
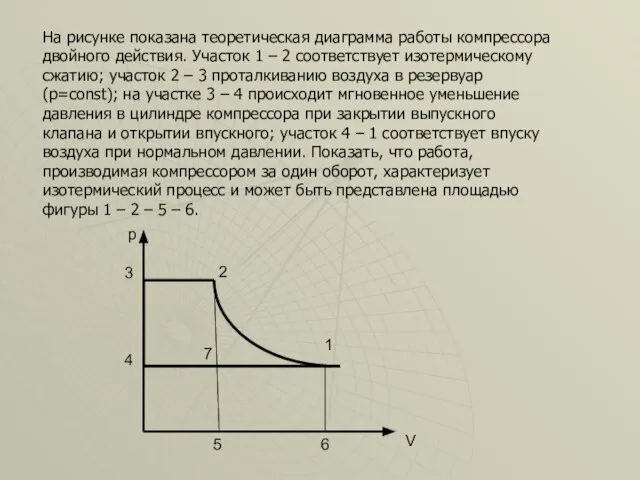
- 40. На рисунке показана теоретическая диаграмма работы компрессора двойного действия. Участок 1 – 2 соответствует изотермическому сжатию;
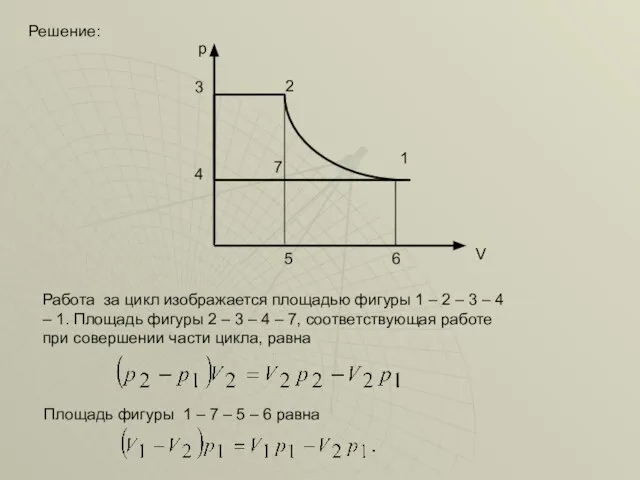
- 41. Решение: p V 2 3 6 5 4 7 Работа за цикл изображается площадью фигуры 1
- 42. Так как точки 1 и 2 лежат на одной изотерме, то Следовательно, то есть за один
- 43. ЗАДАЧА №10
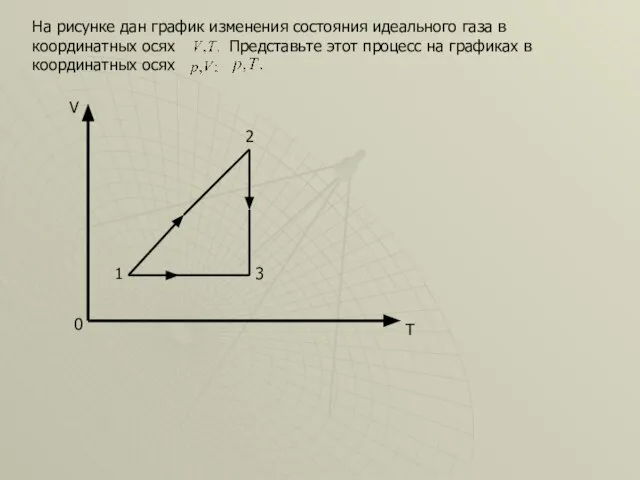
- 44. На рисунке дан график изменения состояния идеального газа в координатных осях Представьте этот процесс на графиках
- 45. 0 V T 2 3 1 Решение. Поскольку на осях координат не указан масштаб, то по
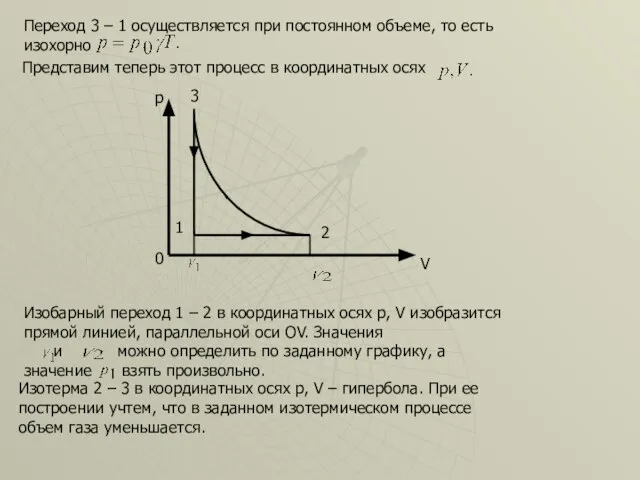
- 46. Переход 3 – 1 осуществляется при постоянном объеме, то есть изохорно Представим теперь этот процесс в
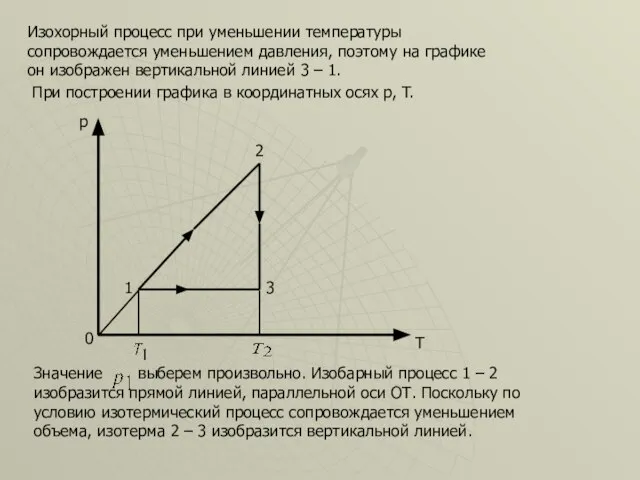
- 47. Изохорный процесс при уменьшении температуры сопровождается уменьшением давления, поэтому на графике он изображен вертикальной линией 3
- 48. Точка 3 должна находиться на изотерме - 2 и на изохоре, часть которой О – 1
- 49. ЗАДАЧА №11
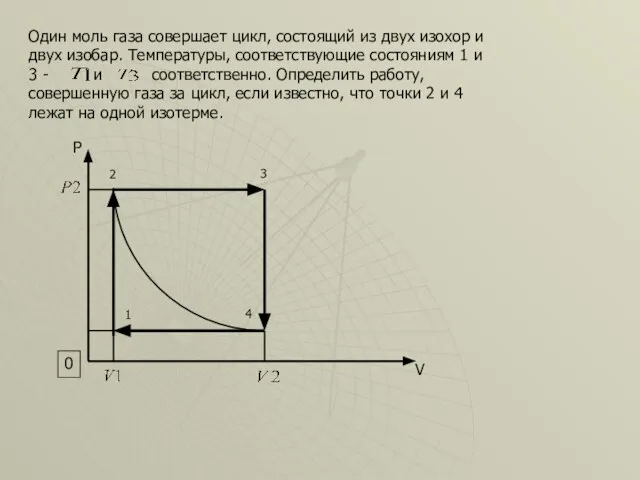
- 50. Один моль газа совершает цикл, состоящий из двух изохор и двух изобар. Температуры, соответствующие состояниям 1
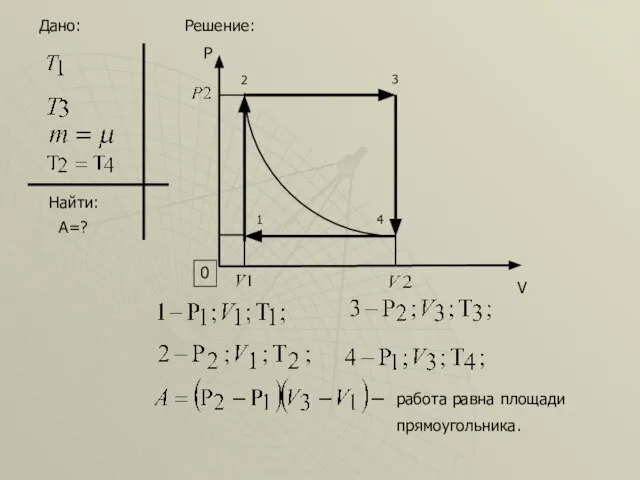
- 51. Дано: Найти: А=? P V 0 1 2 3 4 Решение: работа равна площади прямоугольника.
- 52. Так как (1) Уравнение Клайперона-Менделеева: ( так как ) (2) (3) (4) Из Преобразуем уравнение для
- 54. Скачать презентацию


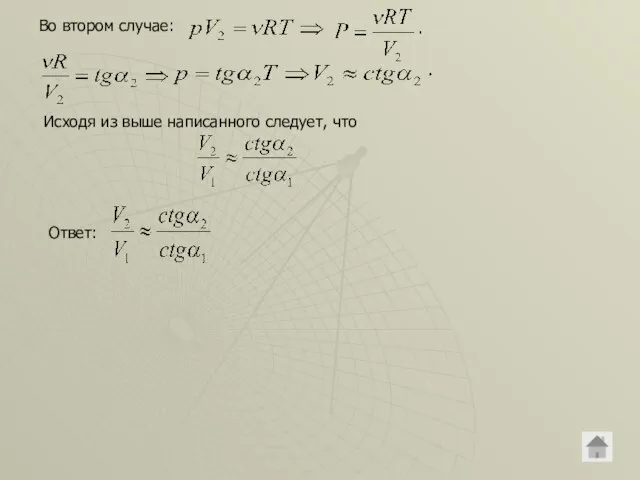
















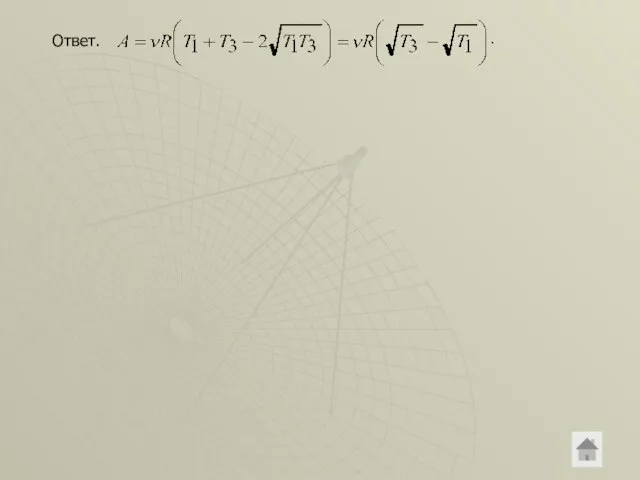







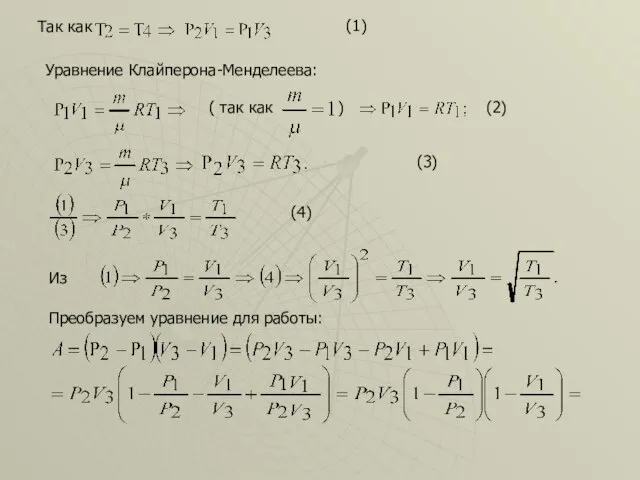
 Отражение звука. Эхо. Звуковой резонанс
Отражение звука. Эхо. Звуковой резонанс Энергия - это жизнь
Энергия - это жизнь Подготовка к ремонту машин необходимого оборудования, инструментов, приспособлений и материалов
Подготовка к ремонту машин необходимого оборудования, инструментов, приспособлений и материалов Виды транспорта
Виды транспорта Подвижной состав автотранспорта
Подвижной состав автотранспорта Силы в механике
Силы в механике Презентация на тему Зрение
Презентация на тему Зрение  Механизмы распределения мощности
Механизмы распределения мощности История телеграфа
История телеграфа Физико-химические МУН. Лекция 6
Физико-химические МУН. Лекция 6 Изменение импульса механической системы
Изменение импульса механической системы Три состояния вещества
Три состояния вещества Радиоактивность. Модели атомов. 9 класс
Радиоактивность. Модели атомов. 9 класс Технологический процесс монтажа устройства для формовки протектора
Технологический процесс монтажа устройства для формовки протектора Техническая механика
Техническая механика Центр тяжести.Виды равновесия (10 класс)
Центр тяжести.Виды равновесия (10 класс) Презентация на тему Связь в России
Презентация на тему Связь в России  Закон сохранения механической энергии. 7 класс
Закон сохранения механической энергии. 7 класс Волновые явления (11 класс)
Волновые явления (11 класс) Масштаб аэрофотоснимков
Масштаб аэрофотоснимков Электромагнитная природа света. Интерференция света. Лекции 12-13
Электромагнитная природа света. Интерференция света. Лекции 12-13 Презентация на тему Первоначальные сведения о строении вещества
Презентация на тему Первоначальные сведения о строении вещества  Молния. Гроза́
Молния. Гроза́ ЭДС индукции
ЭДС индукции Основы волновой теории распространения сейсмических колебаний. Сейсмические волны (лекция№15)
Основы волновой теории распространения сейсмических колебаний. Сейсмические волны (лекция№15) Идеальный газ
Идеальный газ Презентация на тему Скорость
Презентация на тему Скорость 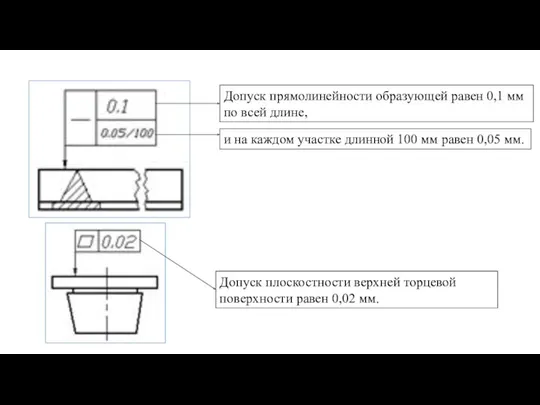 Отклонения формы и расположения
Отклонения формы и расположения