Двугранный угол (10-11 класс) - презентация по Геометрии_

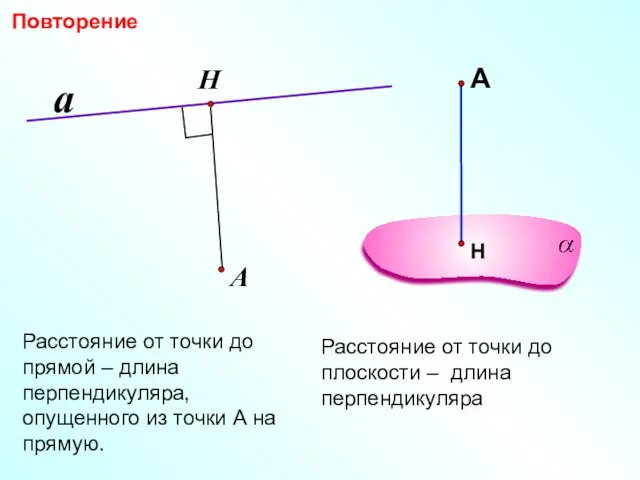
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки А на прямую.
a
А
Расстояние от точки до плоскости – длина перпендикуляра
Повторение
А

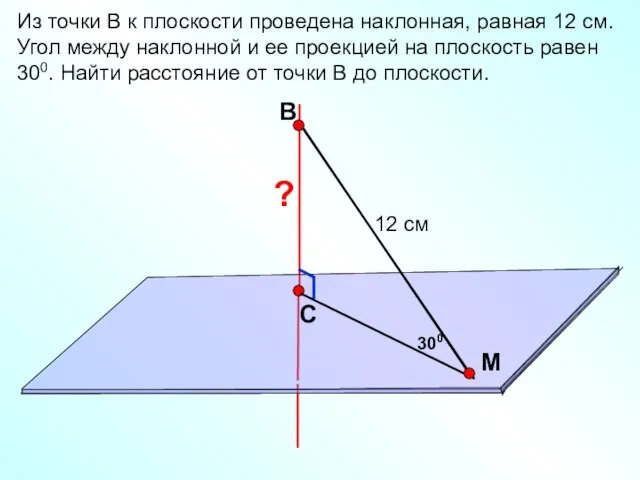
В
С
M
Из точки В к плоскости проведена наклонная, равная 12 см. Угол между наклонной и ее проекцией на плоскость равен 300. Найти расстояние от точки В до плоскости.
12 см
300
?

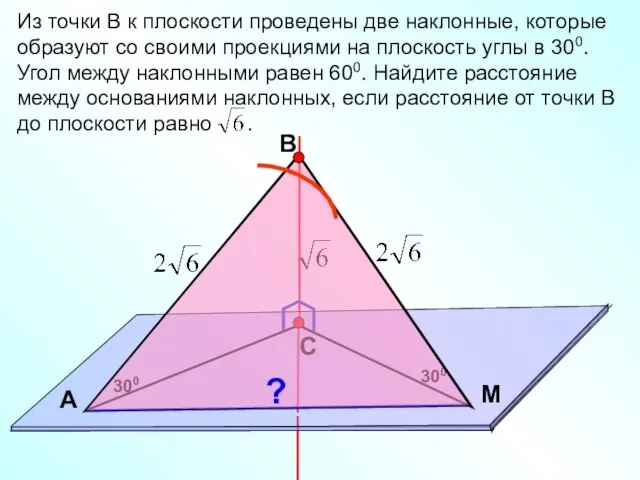
В
С
M
А
Из точки В к плоскости проведены две наклонные, которые образуют со своими проекциями на плоскость углы в 300. Угол между наклонными равен 600. Найдите расстояние между основаниями наклонных, если расстояние от точки В до плоскости равно .
300
300
?

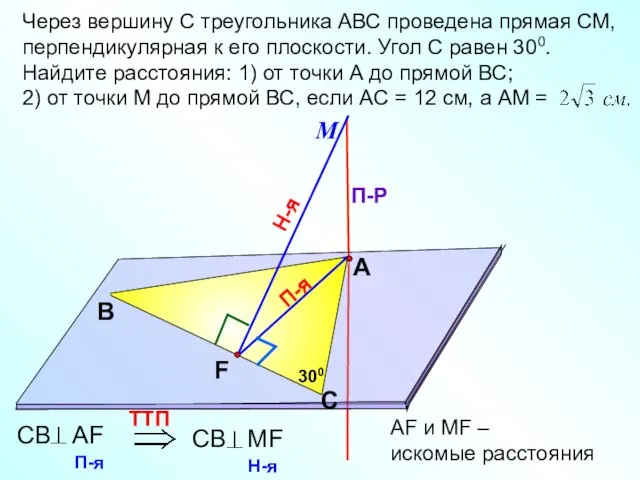
П-я
Через вершину С треугольника АВС проведена прямая СМ, перпендикулярная к его плоскости. Угол С равен 300. Найдите расстояния: 1) от точки А до прямой ВС;
2) от точки М до прямой ВС, если АС = 12 см, а АМ =
А
В
С
П-Р
Н-я
АF и МF –
искомые расстояния
300

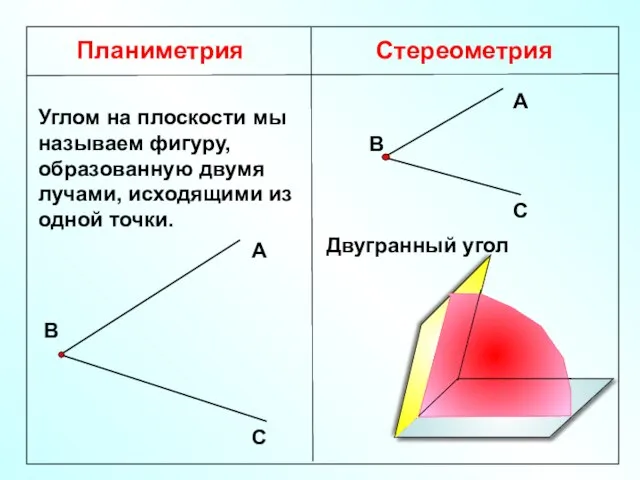
Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.
Двугранный угол

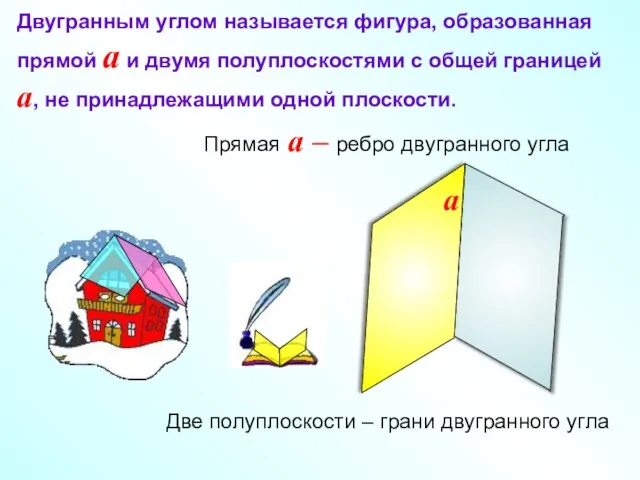
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.
Две полуплоскости – грани двугранного угла
Прямая a – ребро двугранного угла
a

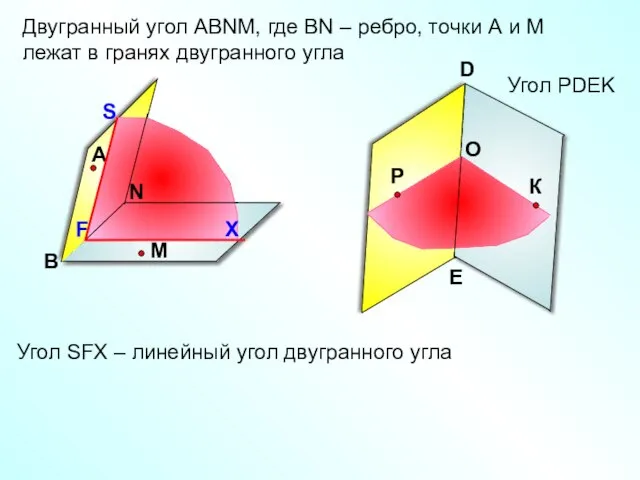
Угол РDEK
Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях двугранного угла
А
В
N
Р
M
К
D
E
Угол SFX – линейный угол двугранного угла

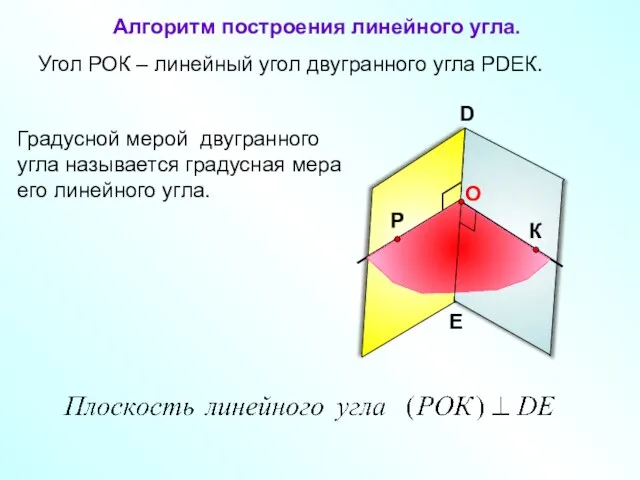
Угол РОК – линейный угол двугранного угла РDEК.
D
E
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Алгоритм построения линейного угла.

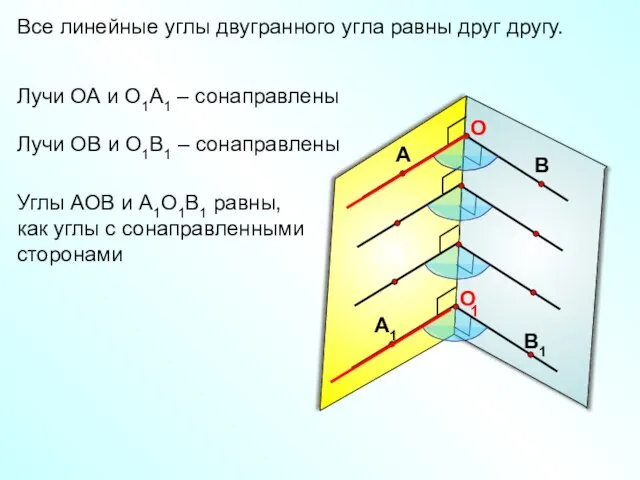
Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными сторонами

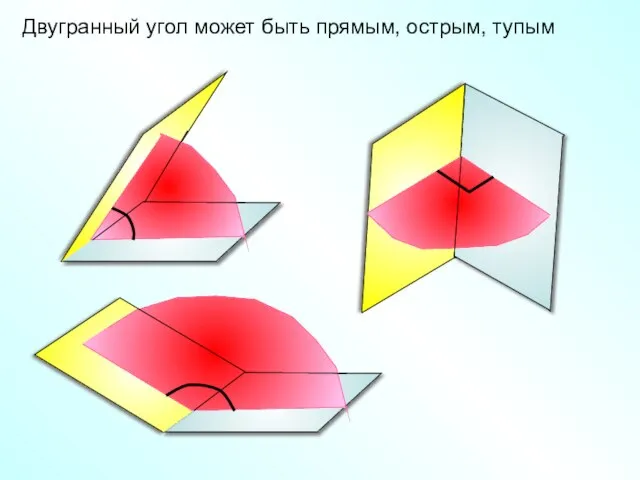
Двугранный угол может быть прямым, острым, тупым

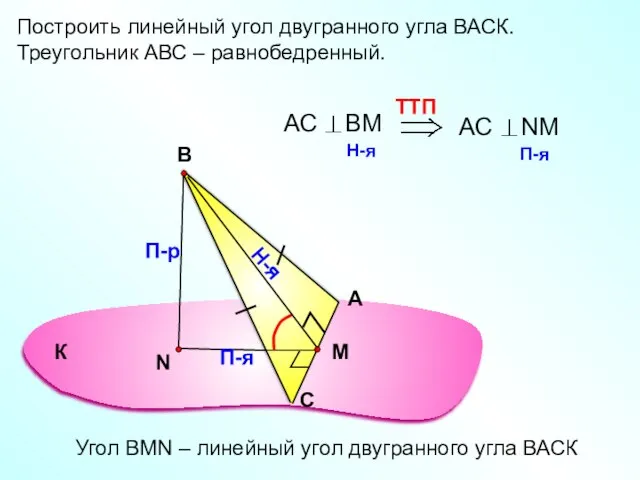
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN – линейный угол двугранного угла ВАСК
К

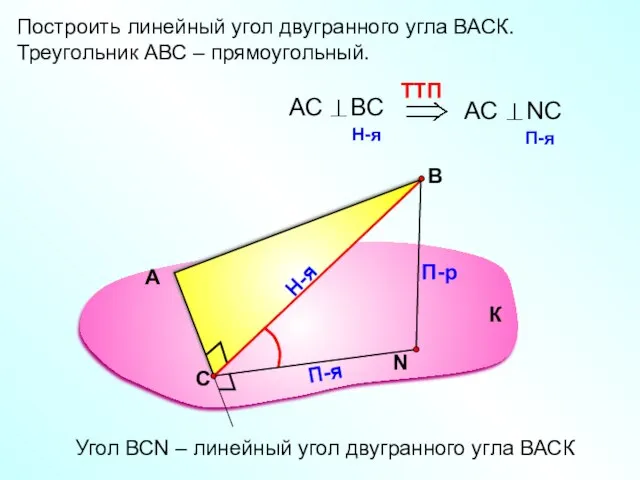
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный угол двугранного угла ВАСК
К
С

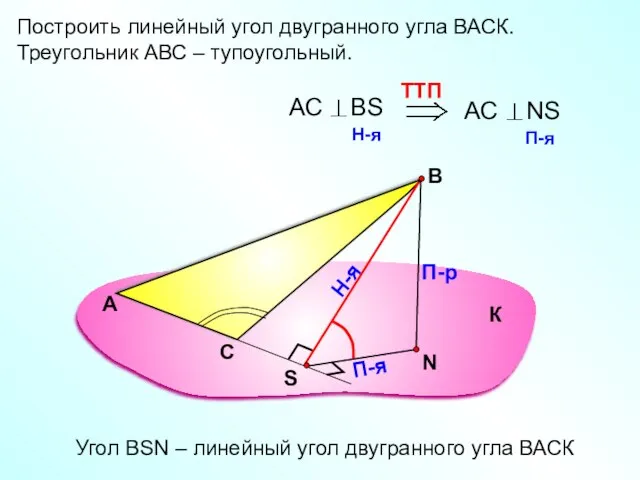
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN – линейный угол двугранного угла ВАСК
К
С

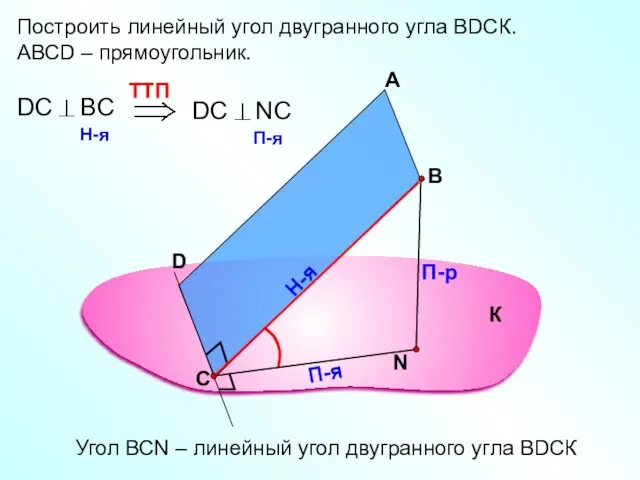
Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный угол двугранного угла ВDСК
К
С
D

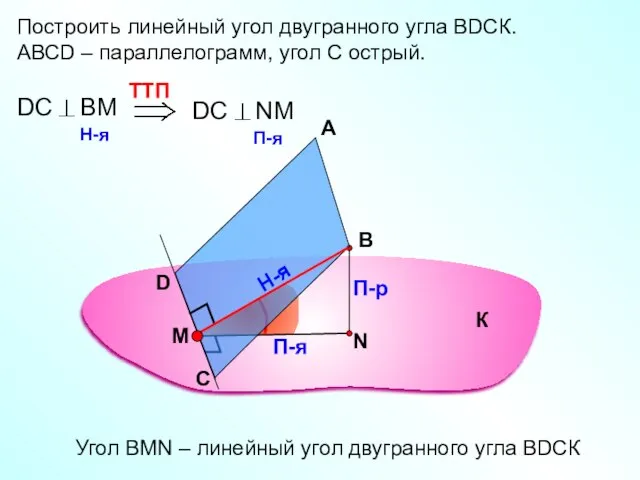
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я

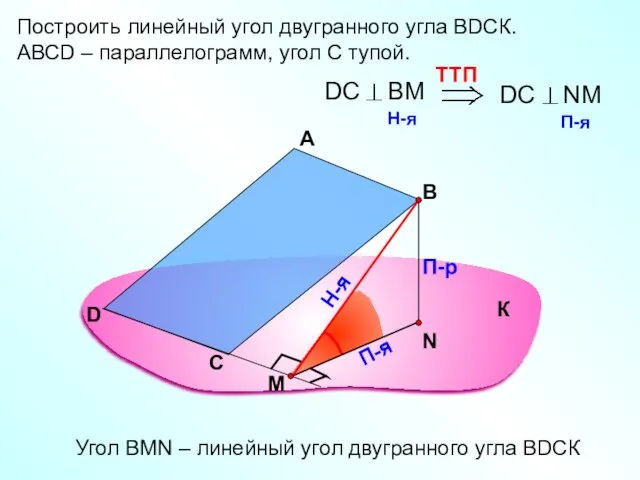
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я

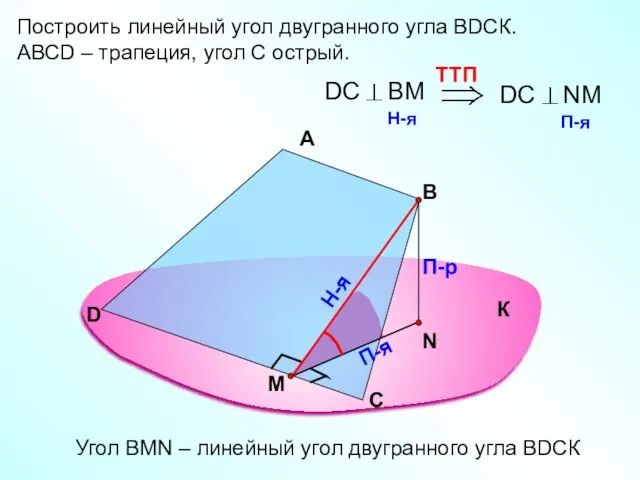
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я

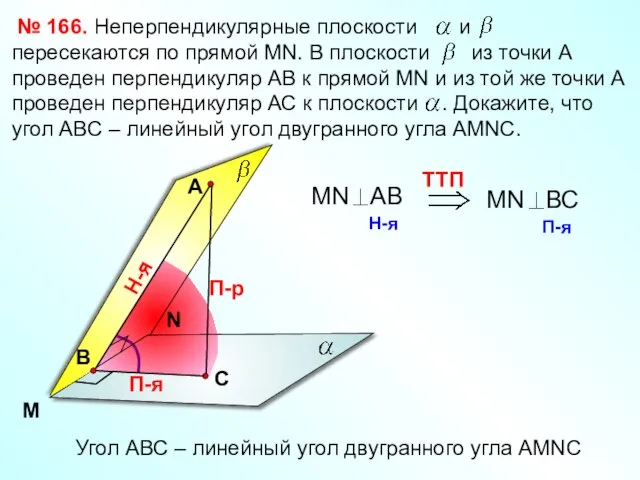
№ 166.
M
N
А
П-р
Н-я
П-я
Угол АВС – линейный угол двугранного угла АМNC

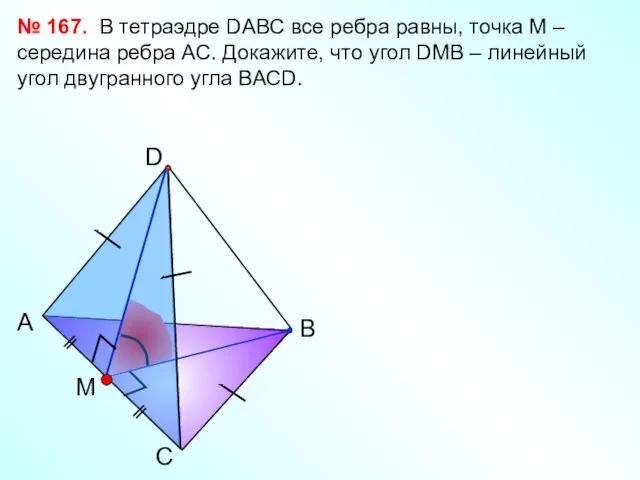
С
А
В
D
M
В тетраэдре DАВС все ребра равны, точка М – середина ребра АС. Докажите, что угол DМВ – линейный угол двугранного угла ВАСD.
№ 167.

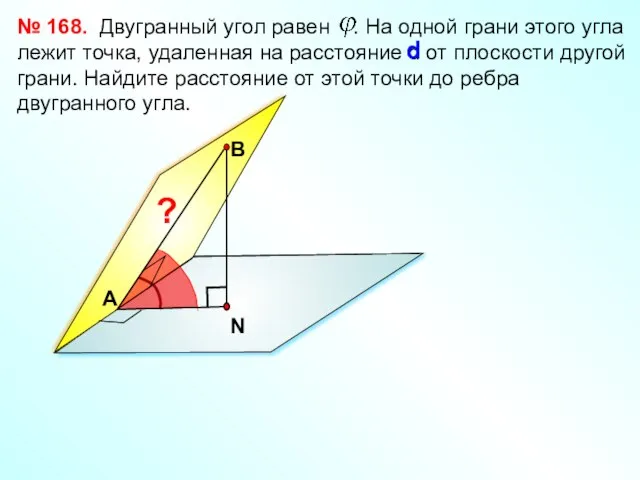
Двугранный угол равен . На одной грани этого угла лежит точка, удаленная на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла.
№ 168.
В
d
А
?