Содержание
- 2. Цели проекта: «Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет». Вильгельм Лейбниц
- 3. Геометрия (от греч. γη - Земля и μετρεω - мера, измерение) - часть математики, изучающая пространственные
- 4. Геометрия - одна из самых древних наук. Важную роль в ее появлении сыграли эстетические потребности людей:
- 5. Геометрия на Востоке Родиной геометрии считают обыкновенно Вавилон и Египет. Греческие писатели единодушно сходятся на том,
- 6. Однако точных сведений о познаниях египтян в области геометрии мы не имеем. Единственным первоисточником, дошедшим до
- 7. Геометрические сведения вавилонян были столь же отрывочны и столь же скудны. Им принадлежит деление окружности на
- 8. Греческие авторы относят появление геометрии в Греции к концу VII в. до н. э. и связывают
- 9. Ионийская школа перенесла геометрию в область гораздо более широких представлений и задач, придала ей теоретический характер
- 10. Пифагор доказал также знаменитую теорему, носящую ныне его имя, согласно которой площадь квадрата, построенного на гипотенузе
- 11. Однако и содержание этой новой дисциплины скоро тоже стали понимать в более широком смысле, который может
- 12. Такие «Начала» по свидетельству Прокла, составили Гиппократ Хиосский, Гиероним Колофонский и др. Ни одно из этих
- 13. Евклид жил в Александрии около 300 года до нашей эры, был современником царя Птоломея I и
- 14. В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более
- 15. Легенды связывают всю защиту Сиракуз с именем Архимеда, который изобретал все новые и новые метательные орудия,
- 16. Французский математик Ж.Дезарг (1593-1662) в связи с развитием учения о перспективе занялся исследованием свойств геометрических фигур
- 17. Тесно связанная с проективной, начертательная геометрия была введена французским математиком Г.Монжем (1746-1818). Эта новая область геометрии
- 18. В 1637 Р.Декарт (1596-1650), французский философ и математик, опубликовал свою Геометрию - первый труд по аналитической
- 19. Неевклидова геометрия Не все написанное в «Началах» Евклидом удовлетворяло живших после него математиков. Одна из аксиом,
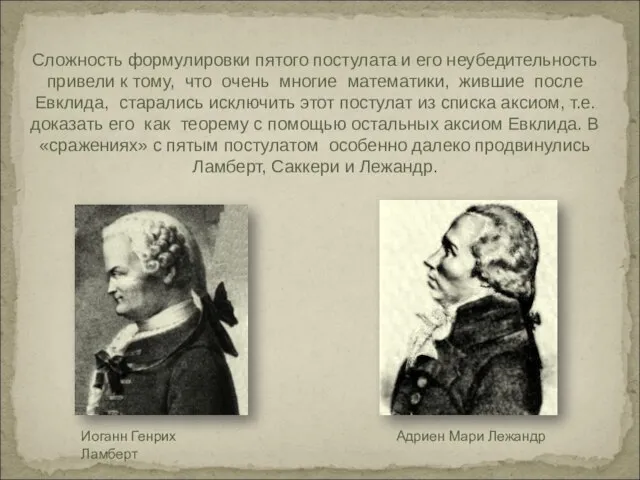
- 20. Сложность формулировки пятого постулата и его неубедительность привели к тому, что очень многие математики, жившие после
- 21. В начале XIX в. в «сражение» вступил русский математик профессор Казанского университета Николай Иванович Лобачевский. Первое
- 22. Венгерский математик Янош Больяй тоже очень интересовался проблемой пятого постулата и добился успеха. Он сумел построить
- 23. Классическая геометрия — геометрия точек, прямых и плоскостей, а также фигур на плоскости и тел в
- 24. Исходя из выше сказанного, геометрия изучает формы, размеры, взаимное расположение предметов независимо от их других свойств:
- 26. Скачать презентацию






















 Правильные многоугольники (9 класс)
Правильные многоугольники (9 класс) Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс
Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс Смотр общественных знаний
Смотр общественных знаний ГИА 2013 Модуль «Геометрия» № 11
ГИА 2013 Модуль «Геометрия» № 11 ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Многообразие многоугольников
Многообразие многоугольников Прямоугольный параллелепипед
Прямоугольный параллелепипед Циклоида
Циклоида Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Треугольники. Третий признак равенства
Треугольники. Третий признак равенства Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Координаты вектора
Координаты вектора Площадь трапеции
Площадь трапеции Координатный метод
Координатный метод Объем тел вращения - презентация по Геометрии
Объем тел вращения - презентация по Геометрии Следствия из аксиом стереометрии Упражнения по теме
Следствия из аксиом стереометрии Упражнения по теме Теорема Пифагора задачи
Теорема Пифагора задачи Правильные многогранники
Правильные многогранники Прямоугольный треугольник 8 класс - презентация по Геометрии___________________________________________________________________________________________________________________
Прямоугольный треугольник 8 класс - презентация по Геометрии___________________________________________________________________________________________________________________ Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Прямоугольный треугольник
Прямоугольный треугольник Многогранники: виды задач и методы их решения (типовые задания С2) - 1
Многогранники: виды задач и методы их решения (типовые задания С2) - 1 Цилиндр и конус
Цилиндр и конус Правильный додекаэдр
Правильный додекаэдр Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Симметрия
Симметрия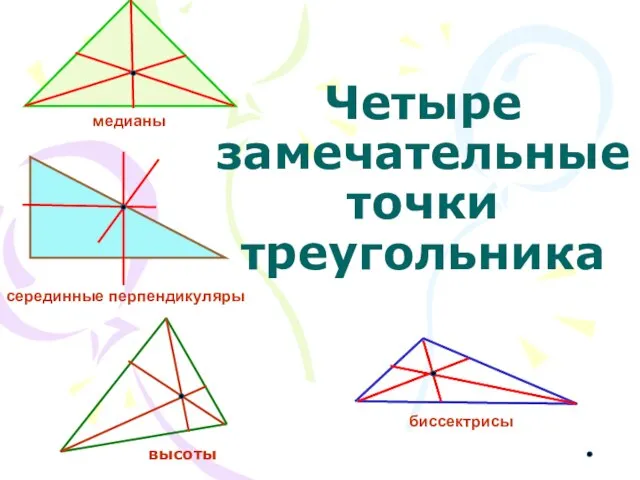 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника