Содержание
- 2. Уравнение прямой в пространстве Прямую, проходящую через точку A0(x0,y0,z0) с направляющим вектором (a,b,c) можно задавать параметрическими
- 3. Упражнение 1 Какими уравнениями задаются координатные прямые?
- 4. Упражнение 2 Напишите параметрические уравнения прямой, проходящей через точку А(1,-2,3) с направляющим вектором, имеющим координаты (2,3,-1).
- 5. Упражнение 3 Напишите параметрические уравнения прямой, проходящей через точки А1(-2,1,-3), А2(5,4,6).
- 6. Упражнение 4 Напишите параметрические уравнения прямой, проходящей через точку M(1,2,-3) и перпендикулярную плоскости x + y
- 7. Упражнение 5 В каком случае параметрические уравнения определяют перпендикулярные прямые? Ответ: Если выполняется равенство a1a2+b1b2+c1c2=0.
- 8. Упражнение 6 Определите взаимное расположение прямой, задаваемой уравнениями и плоскости, задаваемой уравнением x – 3y +
- 9. Упражнение 7 Найдите координаты точки пересечения плоскости 2x – y + z – 3 = 0
- 10. Упражнение 8 Определите взаимное расположение прямых, задаваемых уравнениями Ответ: Перпендикулярны.
- 11. Упражнение 9 Точка движется прямолинейно и равномерно в направлении вектора (1,2,3). В начальный момент времени t
- 12. Упражнение 10 Параметрические уравнения движения материальной точки в пространстве имеют вид Найдите скорость.
- 13. Упражнение 11 Точка движется прямолинейно и равномерно. В момент времени t = 2 она имела координаты
- 15. Скачать презентацию












 Что такое окружность? - презентация по Геометрии_
Что такое окружность? - презентация по Геометрии_ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Плоскость
Плоскость Преобразования на плоскости
Преобразования на плоскости Теоремы синусов и косинусов
Теоремы синусов и косинусов Музей истории четырёхугольников
Музей истории четырёхугольников Проецирование (8 класс)
Проецирование (8 класс)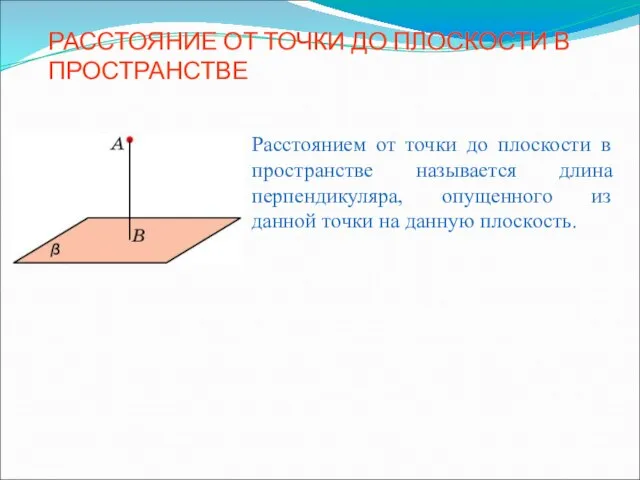 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Площадь прямоугольного треугольника
Площадь прямоугольного треугольника Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Десять решений одной задачи
Десять решений одной задачи Геометрия Лобачевского
Геометрия Лобачевского Многогранники в архитектуре
Многогранники в архитектуре вид разреза сечения
вид разреза сечения Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Свойства пирамиды с равными боковыми ребрами
Свойства пирамиды с равными боковыми ребрами Теорема Пифагора 7-9 класс
Теорема Пифагора 7-9 класс Выделение элементов и свойств геометрических фигур - презентация по Геометрии_
Выделение элементов и свойств геометрических фигур - презентация по Геометрии_ Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Многогранники вокруг нас
Многогранники вокруг нас Описанная и вписанная окружность
Описанная и вписанная окружность Прямоугольный треугольник 8 класс - презентация по Геометрии___________________________________________________________________________________________________________________
Прямоугольный треугольник 8 класс - презентация по Геометрии___________________________________________________________________________________________________________________ Построение диаграмм и графиков
Построение диаграмм и графиков Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна
Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна Флексагоны
Флексагоны В мире плоскостей
В мире плоскостей Сфера и шар 9 класс
Сфера и шар 9 класс Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области