Содержание
- 2. целью работы показать практические возможности применения квадрата как геометрической фигуры.
- 3. Задачи: углубить имеющие знания и приобрести новые; познакомить с особенностями периметра и площади квадрата в сравнении
- 4. Что такое квадрат? Квадратом называется прямоугольник, у которого все стороны равны.
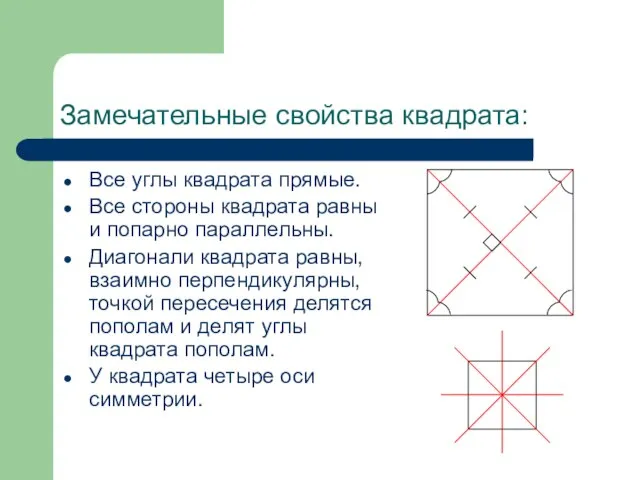
- 5. Замечательные свойства квадрата: Все углы квадрата прямые. Все стороны квадрата равны и попарно параллельны. Диагонали квадрата
- 6. Чем квадрат "лучше" других четырёхугольников? Площадь квадрата больше площади любого прямоугольника с тем же периметром.
- 7. Магический квадрат третьего порядка Здесь изображен единственный магический квадрат третьего порядка. Если ты найдешь семь других
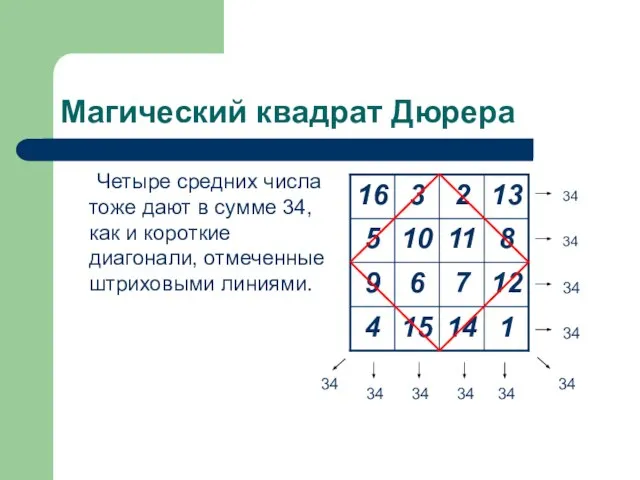
- 8. Магический квадрат Дюрера Четыре средних числа тоже дают в сумме 34, как и короткие диагонали, отмеченные
- 9. Как Абул Вефа составил квадрат из трёх равных квадратов? Он разрезал квадраты I и II по
- 10. Задача на разрезание квадрата #1(Результат) Но теперь надо еще показать, что шесть разрезов можно в действительности
- 11. Игра с квадратом «Край в край» Сколько фигур разной формы (не считая отражений) можно получить соединяя:
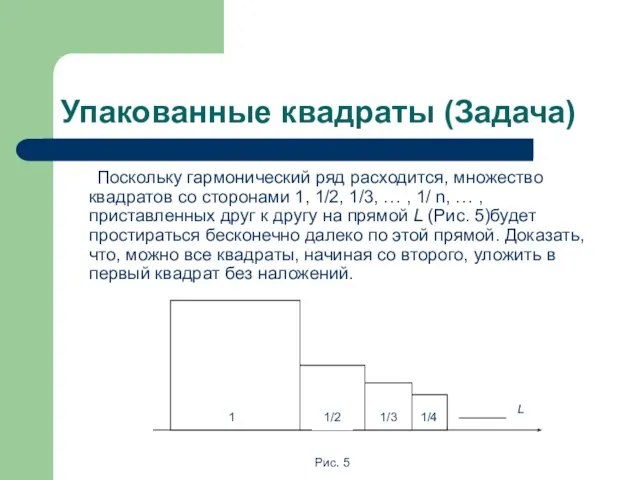
- 12. Упакованные квадраты (Задача) Поскольку гармонический ряд расходится, множество квадратов со сторонами 1, 1/2, 1/3, … ,
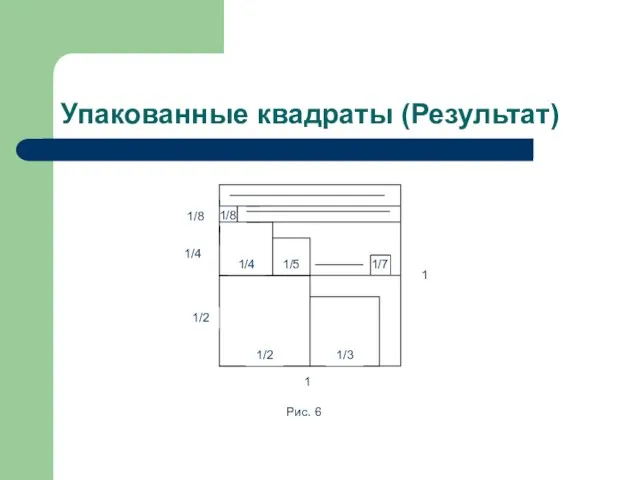
- 13. Упакованные квадраты (Результат) Рис. 6 1/7 1/8 1/2 1/3 1 1 1/2 1/4 1/8 1/4 1/5
- 14. Танграмы Эта головоломка изобретена в Древнем Китае (у нас она сейчас распространена под названием «Пифагор».). Из
- 15. Танграмы (Изображения 1)
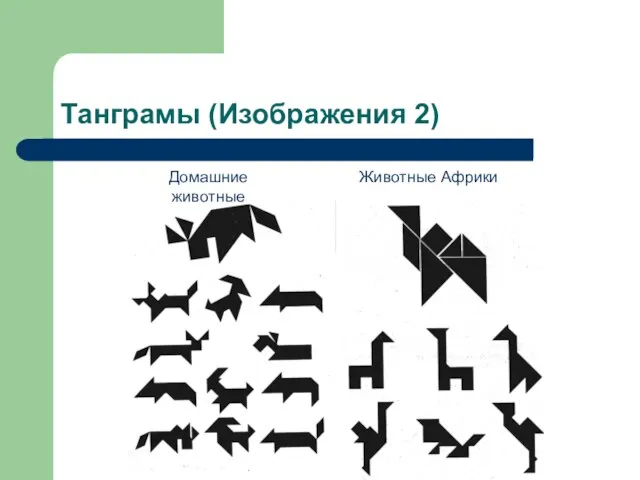
- 16. Танграмы (Изображения 2) Домашние животные Животные Африки
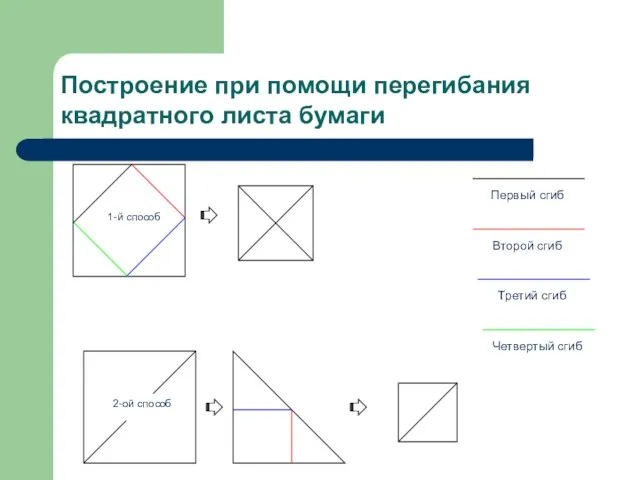
- 17. Построение при помощи перегибания квадратного листа бумаги 1-й способ 2-ой способ Первый сгиб Второй сгиб Четвертый
- 19. Скачать презентацию










 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием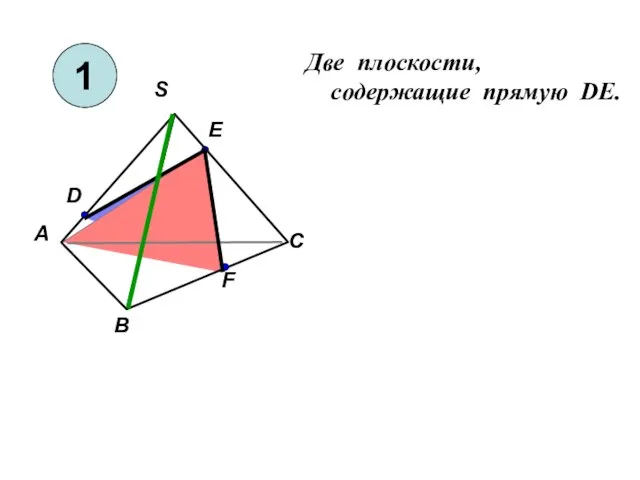 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия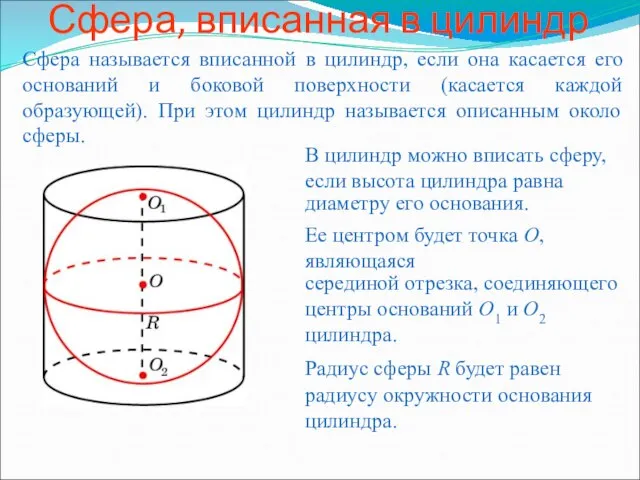 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика