Содержание
- 2. Задача: Периметр квадрата РТМК равен 48 см. Найдите площадь пятиугольника РТМОК Решение: РТ=ТМ=МK=РK=48:4=12 (см); SPTMK =
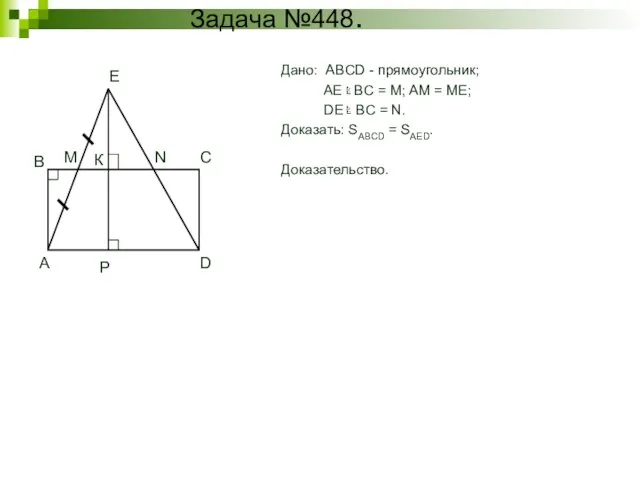
- 3. Задача №448. Дано: ABCD - прямоугольник; AE BC = M; AM = ME; DE BC =
- 4. Любые два равновеликих многоугольника равносоставленны. Теорема Бойяи – Гервина. Ф.Бойяи – венгерский математик, доказал это утверждение
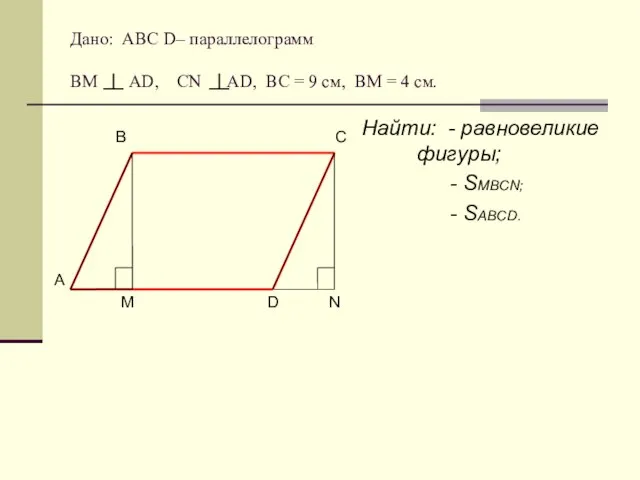
- 5. Дано: АВС D– параллелограмм ВМ АD, CN AD, BC = 9 cм, ВМ = 4 см.
- 6. Тема: Площадь параллелограмма и треугольника.
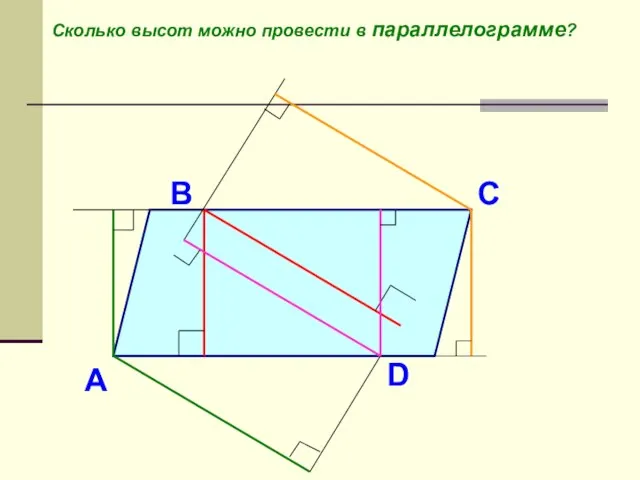
- 7. А D С В Сколько высот можно провести в параллелограмме?
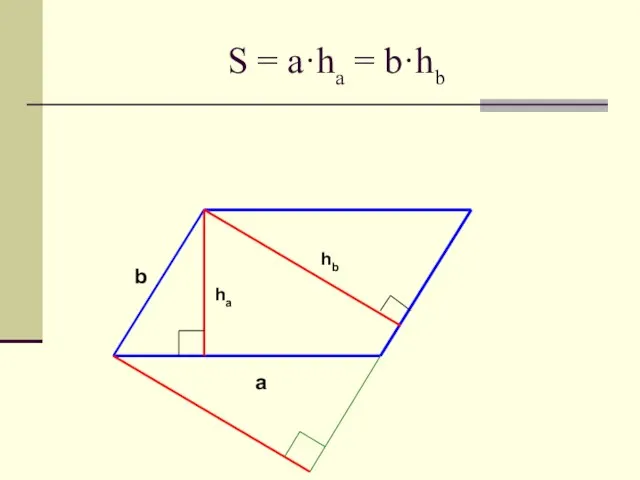
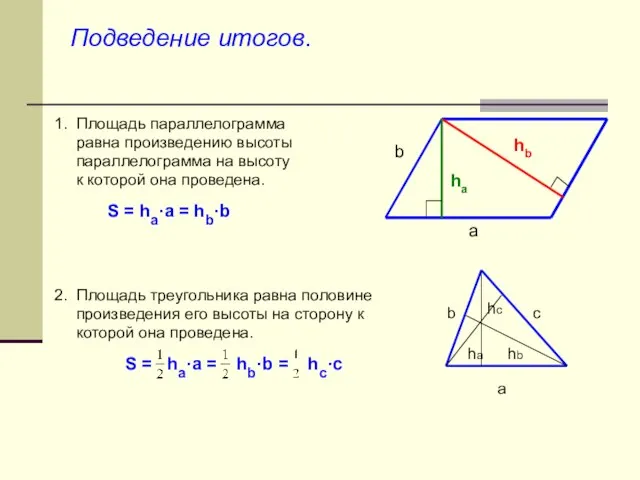
- 8. S = a·ha = b·hb
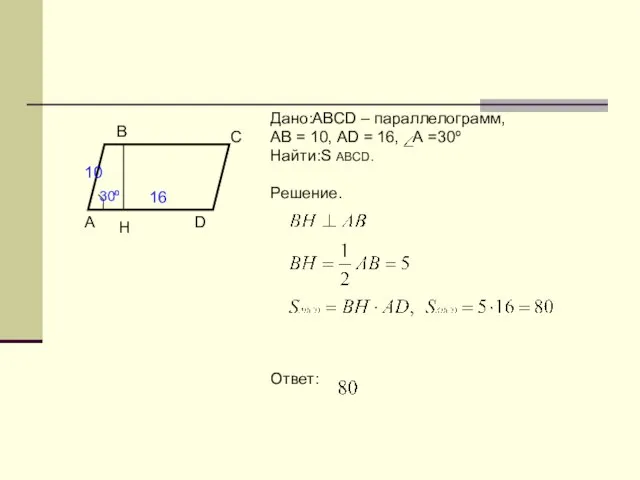
- 9. Дано:ABCD – параллелограмм, АВ = 10, АD = 16, А =30º Найти:S ABCD. Решение. Ответ: 30º
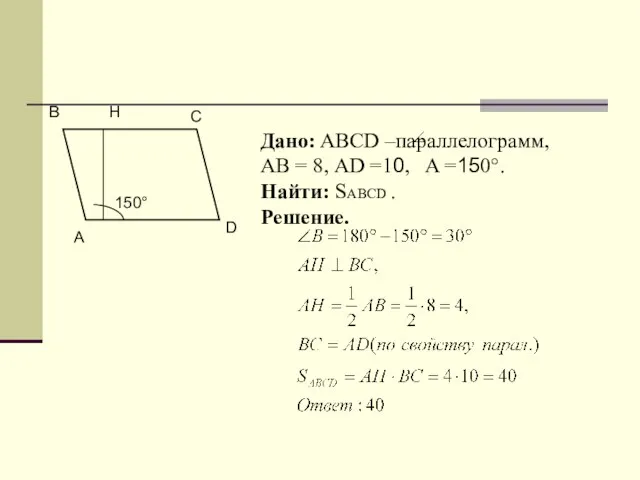
- 10. А B D C H 150° Дано: ABCD –параллелограмм, АВ = 8, АD =10, A =150°.
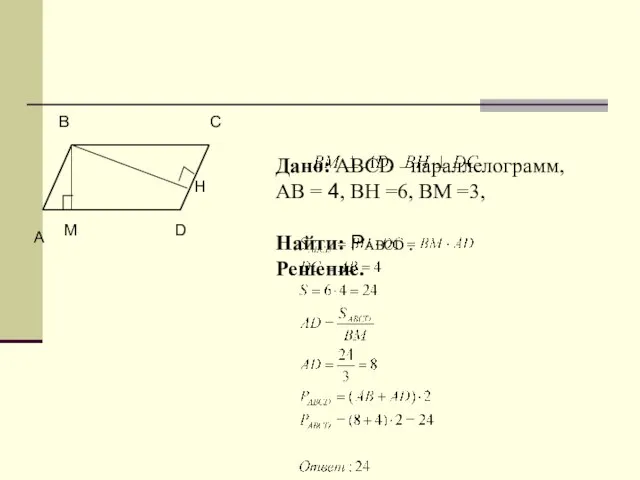
- 11. Дано: ABCD –параллелограмм, АВ = 4, ВН =6, ВМ =3, Найти: РABCD . Решение. C
- 12. Домашнее задание: Вопросы для повторения к главе VI 4 – 5; № 459(б), № 469. Вывести
- 13. Подведение итогов. 2. Площадь треугольника равна половине произведения его высоты на сторону к которой она проведена.
- 15. Скачать презентацию




 Симметрия
Симметрия Стереометрия в образах
Стереометрия в образах Прямоугольный параллелепипед (5 класс)
Прямоугольный параллелепипед (5 класс) «Чтение графиков. ЕГЭ» ЮВАО
«Чтение графиков. ЕГЭ» ЮВАО Цилиндр и конус
Цилиндр и конус Двумерный симплекс история его изучения
Двумерный симплекс история его изучения Длина окружности. Площадь круга
Длина окружности. Площадь круга Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А.
Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А. Луч и угол (7 класс)
Луч и угол (7 класс) Геометрия.Введение. Аксиоматика.
Геометрия.Введение. Аксиоматика. Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Выделение элементов и свойств геометрических фигур - презентация по Геометрии_
Выделение элементов и свойств геометрических фигур - презентация по Геометрии_ Координаты вектора
Координаты вектора Пифагоровы штаны во все стороны равны
Пифагоровы штаны во все стороны равны Развитие пространственного мышления
Развитие пространственного мышления Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Сфера, вписанная в многогранник
Сфера, вписанная в многогранник Магические квадраты (5 класс)
Магические квадраты (5 класс) Равнобедренная трапеция
Равнобедренная трапеция Площади фигур. Теорема Пифагора
Площади фигур. Теорема Пифагора Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Лобачевский - «Коперник геометрии»
Лобачевский - «Коперник геометрии» Длина отрезка
Длина отрезка Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Геометрия в архитектуре
Геометрия в архитектуре Сечения
Сечения Функция у = х п и ее свойства
Функция у = х п и ее свойства