Прямоугольные треугольники 7 класс

Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов).
Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Связанные определения
Сторона, противоположная прямому углу, называется гипотенузой (сторона с на рисунке выше).
Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.

Признаки равенства прямоугольных треугольников
По двум катетам
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
А
В
С
А1
С1
В1
Катет В-С равен катету В1-С1, следовательно АВС = А1в1С1

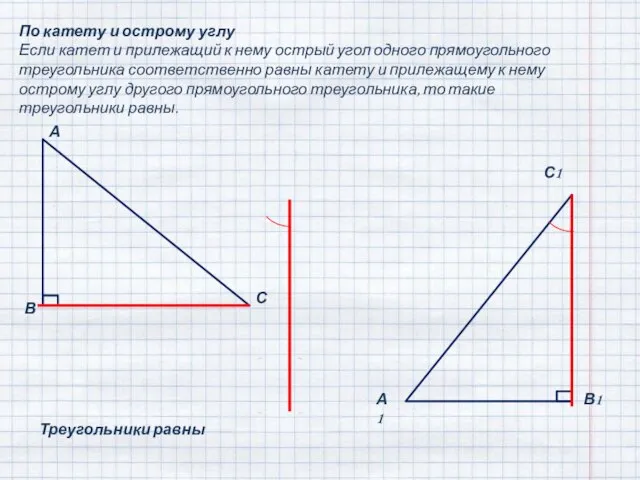
По катету и острому углу
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
А
С
В
С1
В1
А1
Треугольники равны

Свойства
Далее предполагаем, что а и b длины катетов, а с длина гипотенузы
Теорема Пифагора -
Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,
Для медиан , : и выполняется следующее соотношение
В частности, медиана, падающая на гипотенузу, равна половине гипотенузы.

Задача

Задача №2