Содержание
- 2. Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой
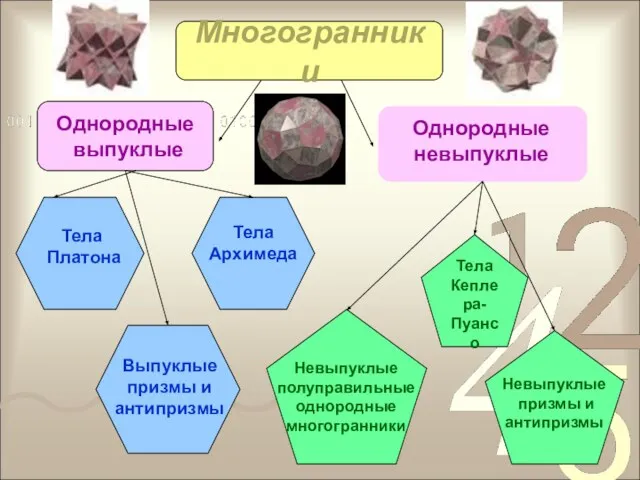
- 3. Многогранники Однородные выпуклые Однородные невыпуклые Тела Архимеда Тела Платона Выпуклые призмы и антипризмы Тела Кеплера- Пуансо
- 4. Правильными многогранниками Называют выпуклые многогранники, все грани и все углы которых равны, причём грани – правильные
- 5. Правильные многогранники Сколько же их существует? Тетраэдр -правильная треугольная пирамида с равными ребрами, ограниченная четырьмя правильными
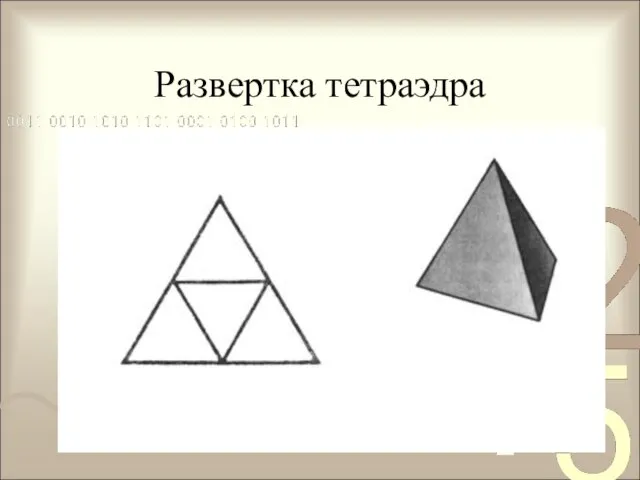
- 6. Развертка тетраэдра
- 7. Правильные многогранники Октаэдр – правильный четырёхугольный диэдр с равными рёбрами, ограниченный восемью правильными треугольниками.
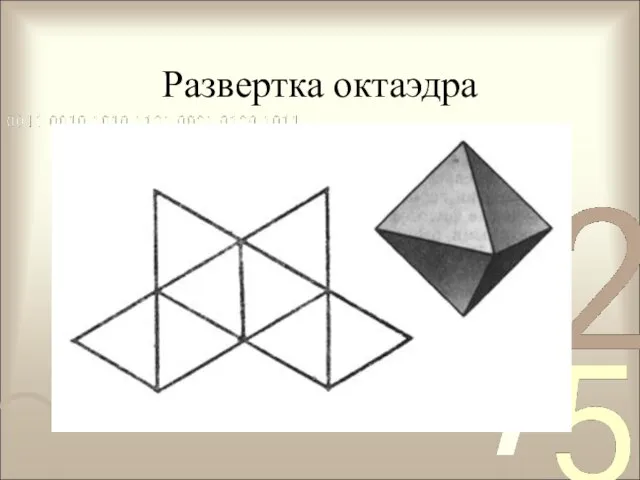
- 8. Развертка октаэдра
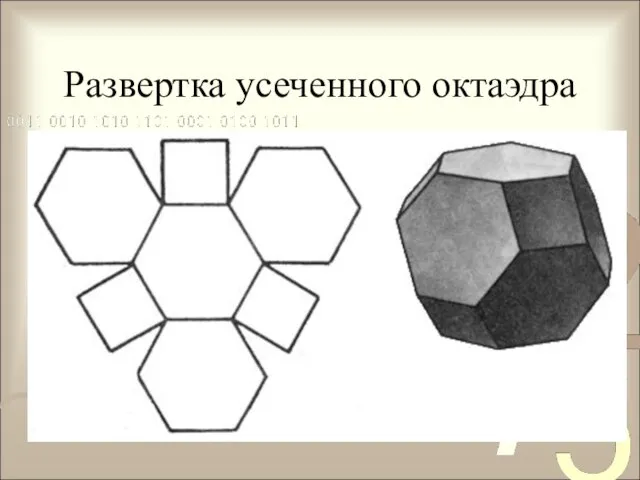
- 9. Развертка усеченного октаэдра
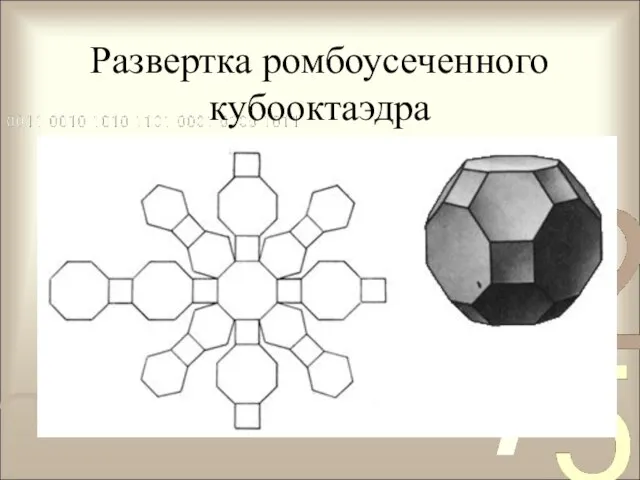
- 10. Развертка ромбоусеченного кубооктаэдра
- 11. Икосаэдр- поверхность, ограниченная двадцатью правильными треугольниками. Правильные многогранники
- 12. Развертка икосаэдра
- 13. Куб(гексаэдр)- правильная четырёхугольная призма с равными рёбрами, ограниченная шестью квадратами. Правильные многогранники
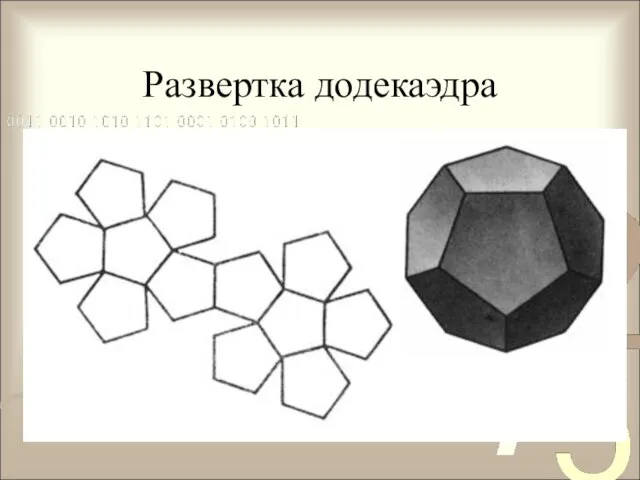
- 14. Правильные многогранники Додекаэдр- поверхность, ограниченная двенадцатью правильными пятиугольниками.
- 15. Развертка додекаэдра
- 16. Сделаем вывод: Мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр
- 17. Тетраэдр Икосаэдр Гексаэдр Додекаэдр Октаэдр
- 18. вода земля воздух огонь Вселенная додекаэдр гексаэдр октаэдр икосаэдр тетраэдр Пифагор
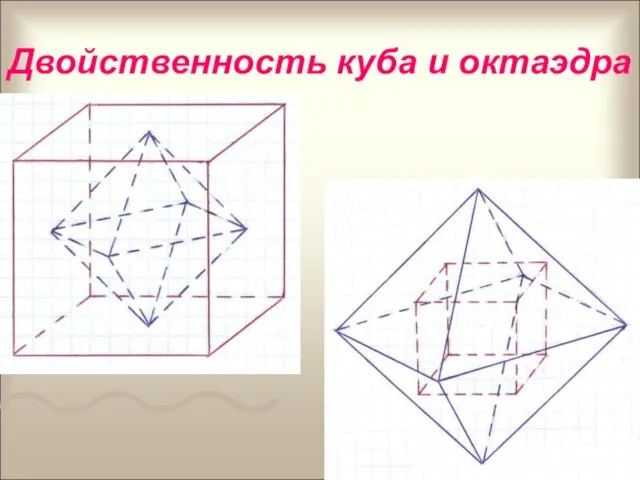
- 19. Двойственность куба и октаэдра
- 20. : «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию
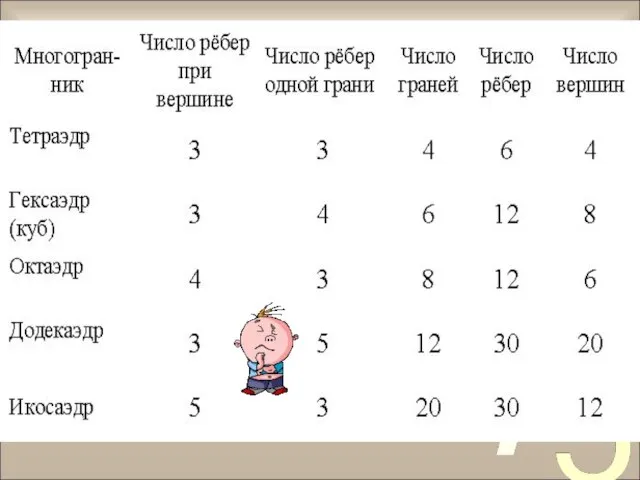
- 21. Число вершин минус число ребер плюс число граней равно двум. Теорема Эйлера В – Р +
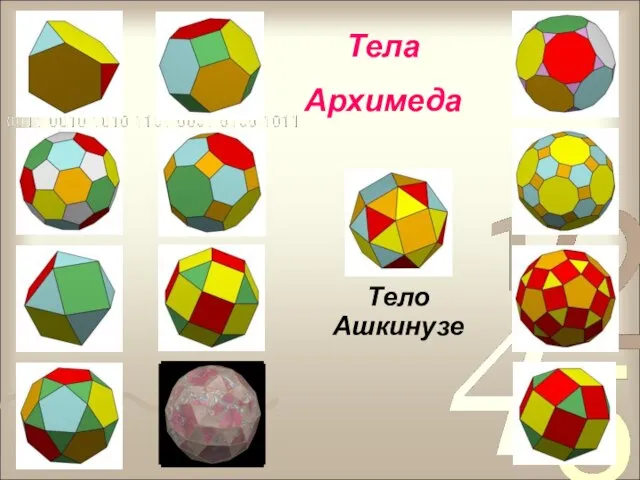
- 23. Тела Архимеда Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы
- 24. Тела Архимеда Тело Ашкинузе
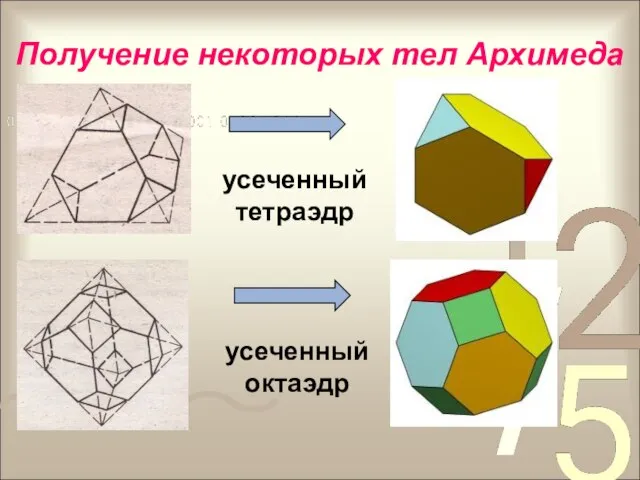
- 25. Получение некоторых тел Архимеда усеченный тетраэдр усеченный октаэдр
- 26. Архимед (287-211 гг. до н.э.)
- 27. Кристаллы Халькопирит Топаз Пирит Авгит Медный купорос
- 28. Тела Кеплера – Пуансо (правильные звездчатые многогранники)
- 29. Большой звездчатый додекаэдр Большой икосаэдр Малый звездчатый додекаэдр Большой додекаэдр
- 30. Получение тел Кеплера - Пуансо Продолжение рёбер додекаэдра приводит к замене каждой грани звёздчатым правильным пятиугольником.
- 31. Иоганн Кеплер (1571-1630)
- 32. Снежинки – звёздчатые многогранники А вы видели тени от снежинок? А вы знаете, как они танцуют
- 33. Многогранники в геологии Икосаэдро- додекаэдрическая структура Земли.
- 34. Многогранники в ювелирном деле
- 36. Скачать презентацию























 Понятие многогранника
Понятие многогранника Путешествие в страну Геометрия
Путешествие в страну Геометрия Правильные многогранники
Правильные многогранники Цилиндр и конус
Цилиндр и конус Четырехугольники
Четырехугольники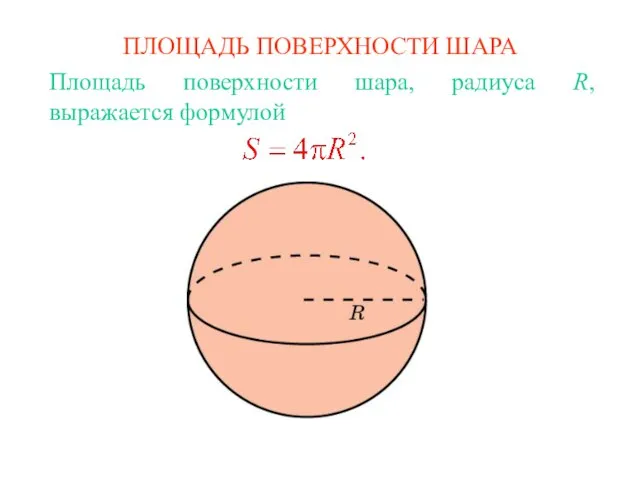 Площадь поверхности шара
Площадь поверхности шара Биссектриса угла
Биссектриса угла Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Параллельный перенос 11 класс - презентация_
Параллельный перенос 11 класс - презентация_ вид разреза сечения
вид разреза сечения Плоскость
Плоскость Понятие объема. Объем призмы
Понятие объема. Объем призмы Теоремы синусов и косинусов
Теоремы синусов и косинусов Стереометрия в образах
Стереометрия в образах Тетраэдр и параллепипед
Тетраэдр и параллепипед Решение треугольников. Измерительные работы на местности
Решение треугольников. Измерительные работы на местности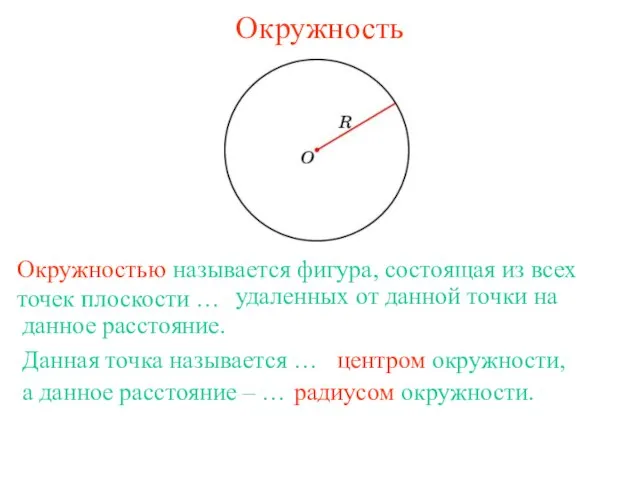 Окружность
Окружность Фракталы – геометрия природы
Фракталы – геометрия природы Многообразие многоугольников
Многообразие многоугольников Приготовьтесь к построению
Приготовьтесь к построению Окружность в аксонометрии
Окружность в аксонометрии Треугольники. Третий признак равенства
Треугольники. Третий признак равенства ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ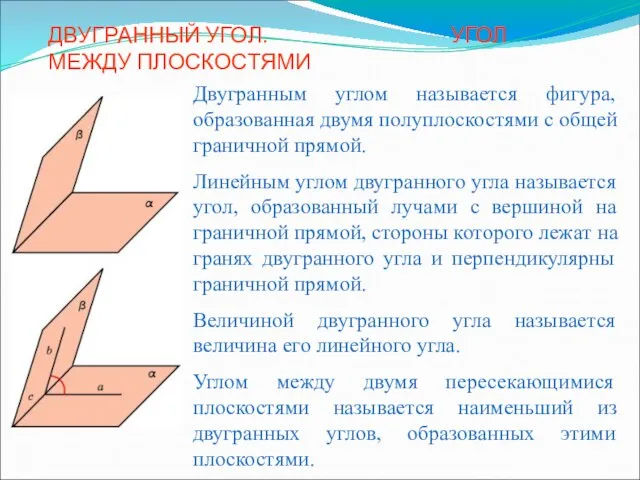 Двугранный угол. Угол между плоскостями4
Двугранный угол. Угол между плоскостями4 Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Урок повторения в 6 классе
Урок повторения в 6 классе В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Симметрия на планете Земля
Симметрия на планете Земля