Слайд 2Цели урока:
Повторить теоретический материал главы «Параллельность прямых и плоскостей».
Проверить усвоение темы в

ходе зачета.
Формирование у учащихся потребности применения знаний в последующем.
Слайд 3Структура урока:
Постановка цели урока
Буквенный диктант
Тест №1
Тест №2
Подведение итогов урока

Слайд 4 Буквенный диктант
1. Две непересекающиеся прямые в пространстве и лежащие в одной

плоскости.
2. Теорема, имеющая значение не столько сама по себе, сколько для дополнения других.
3. Любое множество точек.
Слайд 5 4. Количество прямых, проходящих через точку вне данной прямой, параллельно ей.

5. Прямые, которые не пересекаются и не лежат в одной плоскости.
6. Основная фигура в пространстве.
7. Раздел геометрии, в котором изучаются фигуры в пространстве.
Слайд 6 8. Количество прямых, проходящих через одну точку.
9. Поверхность, составленная из

четырех треугольников.
10. Теорема, более полно характеризующая случаи взаимного расположения фигур в пространстве.
Слайд 71.параллелные
2.лемма
3.фигура
4.одна
5.скрещивающиеся
6.плоскость
7.стереометрия
8.много
9.тетраэдр
10.признак

Слайд 8 1.Какое число сторон может иметь сечение тетраэдра?
а) 3,4 б) 4,5

в) 4 г) 3.
2. Какое число сторон может иметь сечение параллелепипеда?
а) 3,4 б) 4,5,6 в)5,6 г) 3,4,5,6.
3. Используя признак параллельности плоскостей в кубе, укажите число пар параллельных плоскостей.
а) 3 б) 2 в) 1 г) 4.
Слайд 9 4.Каково взаимное расположение прямых в пространстве, если они лежат в одной

плоскости и имеют одну общую точку?
а) пересекаются б) параллельны
в) скрещиваются г) совпадают.
5. Сколько пар ребер, лежащих на скрещивающихся прямых, имеет тетраэдр?
а) 0 б) 1 в) 3 г) 2
Слайд 106. Чему равен угол между параллельными прямыми?
а) 00 б) 900 в)

450 г) 1800
7. Как называется плоскость, по обе стороны от которой имеются точки тетраэдра (параллелепипеда?)
а) α б) сечение в) β г) не знаю
8.Количество прямых, проходящих через две точки?
а) 2 б) много в) 1 г) 0.
Слайд 119.Угол между пересекающимися прямыми?
а) меньший б) 00 в) больший г)развернутый.
10.Что является пересечением

секущей плоскости и граней многогранника?
а) точки б) отрезки в) прямые г) лучи.
Слайд 13 Тест №2
Задача №1. Параллельные прямые АС и BD пересекают плоскость α

в точках А и В. Точки С и D лежат по одну сторону от плоскости α, АС=8 см, BD=6 см, АВ=4 см. а)Докажите, что прямая CD пересекает плоскость α в некоторой точке Е. б)Найдите отрезок ВЕ.
Слайд 14Задача №2. На ребрах DA, DB и DC тетраэдра DABC отмечены точки

M,N и Р так, что DM:МА=DN:NB=DP:PC. Докажите, что плоскости MNP и АВС параллельны. Найдите площадь треугольника MNP, если площадь треугольника АВС равна 10 см2 и DM:МА=2:1.













 Центральная симметрия Занятие 28
Центральная симметрия Занятие 28 Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Построение диаграмм и графиков
Построение диаграмм и графиков Площадь квадрата, прямоугольника, параллелограмма - презентация по Геометрии_
Площадь квадрата, прямоугольника, параллелограмма - презентация по Геометрии_ Скалярное произведение векторов
Скалярное произведение векторов Круг и окружность
Круг и окружность Развитие пространственного мышления
Развитие пространственного мышления Длина отрезка
Длина отрезка Полезные теоремы, следствия и задачи.
Полезные теоремы, следствия и задачи. Перпендикулярные прямые 7 класс
Перпендикулярные прямые 7 класс Красота Фракталов
Красота Фракталов Проект ученицы 5 «А» класса Горбуновой Ксении Учитель: Чижевская М.А.
Проект ученицы 5 «А» класса Горбуновой Ксении Учитель: Чижевская М.А.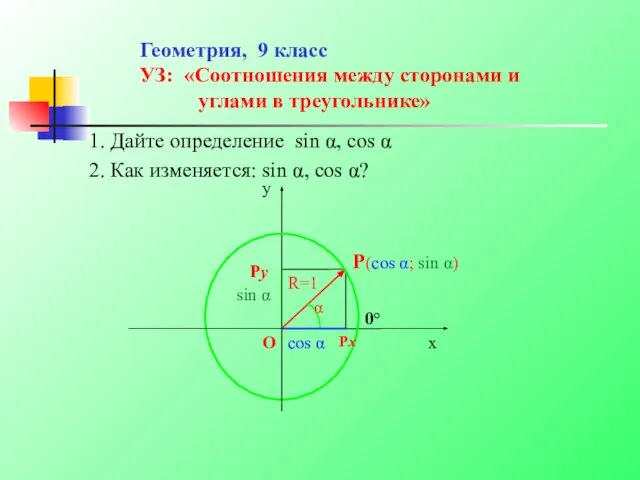 Соотношения между сторонами и углами в треугольнике
Соотношения между сторонами и углами в треугольнике Прямоугольный параллелепипед
Прямоугольный параллелепипед Выделение элементов и свойств геометрических фигур - презентация по Геометрии_
Выделение элементов и свойств геометрических фигур - презентация по Геометрии_ Геометрические задачи на экстремум
Геометрические задачи на экстремум Проекция окружности в аксонометрии - презентация_
Проекция окружности в аксонометрии - презентация_ Объемы пространственных фигур - презентация по Геометрии
Объемы пространственных фигур - презентация по Геометрии Площадь 8 КЛАСС
Площадь 8 КЛАСС Проецирование правильных треугольных и шестиугольных призм
Проецирование правильных треугольных и шестиугольных призм Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Теорема о трех перпендикулярах в задачах 10 заочное обучение
Теорема о трех перпендикулярах в задачах 10 заочное обучение Решение задач по геометрии на готовых чертежах
Решение задач по геометрии на готовых чертежах Циклоида
Циклоида Задачи на готовых чертежах Четырехугольники Презентацию подготовила Команда «ЗВЕЗДОЧКИ» МКУО Тумановская СОШ Руководитель:
Задачи на готовых чертежах Четырехугольники Презентацию подготовила Команда «ЗВЕЗДОЧКИ» МКУО Тумановская СОШ Руководитель:  Учебный проект выполнен учеником 7Б класса МОАУ средней школы №58 Брыляковым Михаилом Руководитель Салангина Е.Д.
Учебный проект выполнен учеником 7Б класса МОАУ средней школы №58 Брыляковым Михаилом Руководитель Салангина Е.Д. Периметр – сумма длин всех сторон.
Периметр – сумма длин всех сторон. Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник