Содержание
- 2. «Симметрия» по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей». Математически строгое представление о симметрии сформировалось сравнительно
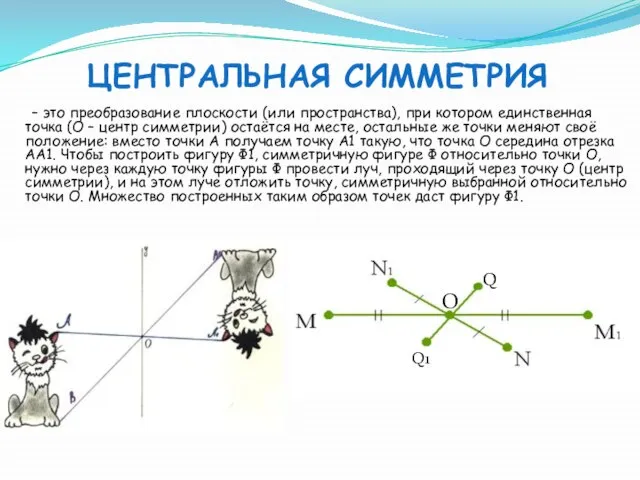
- 3. – это преобразование плоскости (или пространства), при котором единственная точка (О – центр симметрии) остаётся на
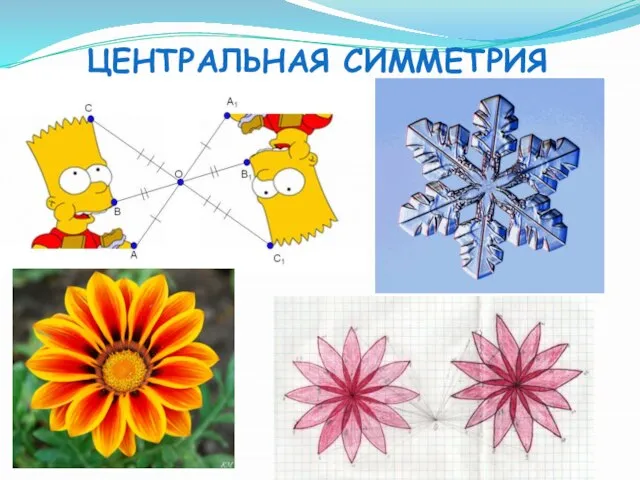
- 4. Центральная симметрия
- 5. – это преобразование плоскости (или пространства), при котором только точки прямой р остаются на месте (эта
- 6. Осевая симметрия
- 7. – это преобразование пространства, при котором только точки одной плоскости сохраняют своё местоположение (α-плоскость симметрии), остальные
- 8. Скользящей симметрией называют композицию симметрии относительно некоторой прямой L и переноса на вектор, параллельный L (этот
- 9. — это симметрия объекта относительно группы преобразований, являющихся композицией преобразования поворота объекта вокруг оси и переноса
- 10. А Д Л М П Т Ф Ш – вертикальная ось В Е З К С
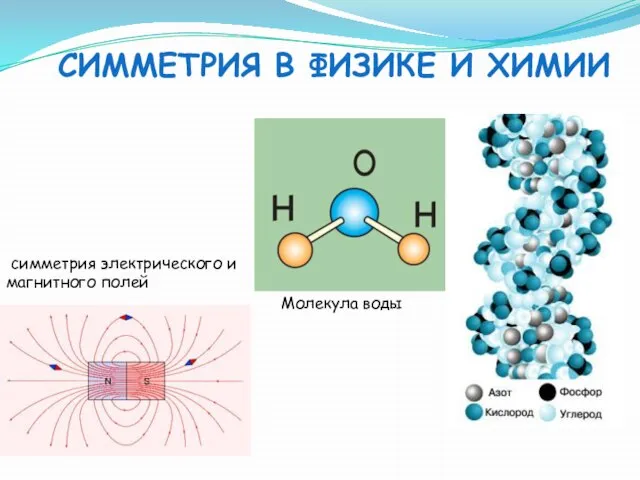
- 11. Симметрия в физике и химии Молекула воды симметрия электрического и магнитного полей
- 12. Симметрия в искусстве
- 13. Симметрия в архитектуре
- 15. Симметрия в природе
- 17. Скачать презентацию











 Площадь трапеции
Площадь трапеции Египетский треугольник
Египетский треугольник Основные свойства простейших геометрических фигур
Основные свойства простейших геометрических фигур 23.01.13 Классная работа. Длина окружности и площадь круга.
23.01.13 Классная работа. Длина окружности и площадь круга. Урок повторения в 6 классе
Урок повторения в 6 классе Задачи на построение сечений
Задачи на построение сечений Сумма углов треугольника
Сумма углов треугольника Преобразования на плоскости
Преобразования на плоскости Геометрия
Геометрия Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Измерение объема тела
Измерение объема тела Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска Теорема Фалеса 8 класс
Теорема Фалеса 8 класс Площадь параллелограмма 8 класс
Площадь параллелограмма 8 класс Периметр – сумма длин всех сторон.
Периметр – сумма длин всех сторон. Длина окружности
Длина окружности Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади Геометрия в древние и новые века
Геометрия в древние и новые века Построение диаграмм и графиков
Построение диаграмм и графиков Равнобедренный треугольник
Равнобедренный треугольник Бриллианты элементарной геометрии - презентация по Геометрии_
Бриллианты элементарной геометрии - презентация по Геометрии_ Прямоугольный параллелепипед (5 класс)
Прямоугольный параллелепипед (5 класс) Шар, вписанный в пирамиду, призму, конус
Шар, вписанный в пирамиду, призму, конус Лист Мёбиуса
Лист Мёбиуса Развёртка куба
Развёртка куба Параллельность в пространстве
Параллельность в пространстве