Расстояние от точки до прямой и плоскости

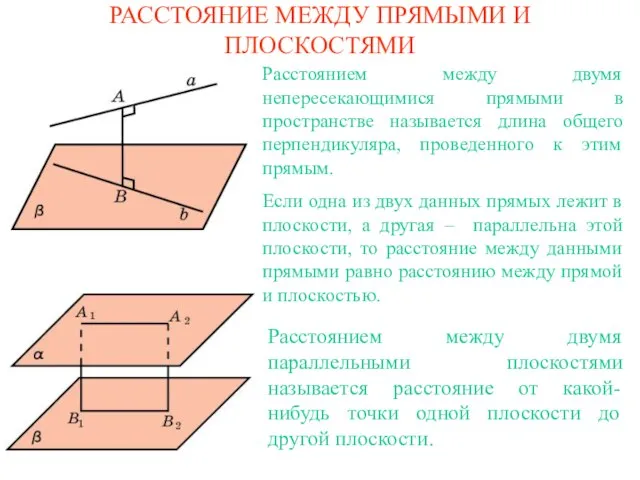
РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ И ПЛОСКОСТЯМИ
Расстоянием между двумя непересекающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного к этим прямым.
Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.
Расстоянием между двумя параллельными плоскостями называется расстояние от какой-нибудь точки одной плоскости до другой плоскости.

Упражнение 1
Из точки А, не принадлежащей плоскости α, проведена наклонная к этой плоскости. Определите угол между этой наклонной и плоскостью α, если расстояние от точки А до плоскости α: а) равно ортогональной проекции наклонной; б) в два раза меньше самой наклонной.
Ответ: а) 45о;
б) 30о.

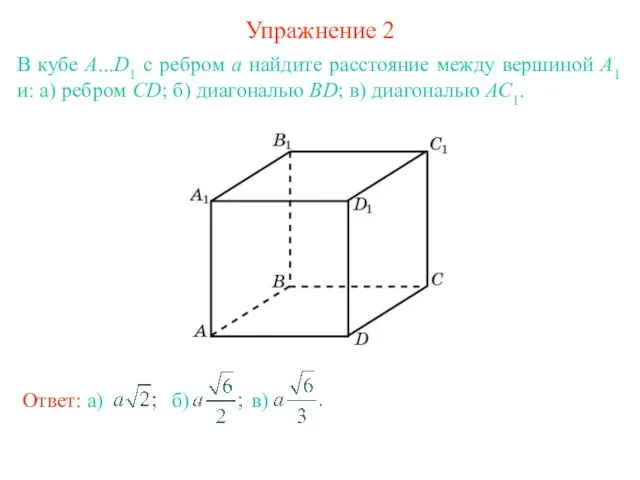
Упражнение 2
В кубе А...D1 с ребром а найдите расстояние между вершиной А1 и: а) ребром CD; б) диагональю BD; в) диагональю АС1.

Упражнение 3
Чему равно расстояние между параллельными гранями в кубе?
Ответ: Ребру куба.

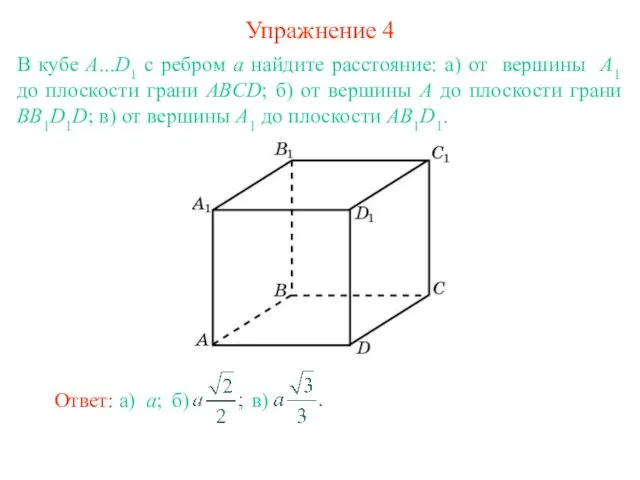
Упражнение 4
В кубе A...D1 с ребром а найдите расстояние: а) от вершины А1 до плоскости грани ABCD; б) от вершины А до плоскости грани BB1D1D; в) от вершины А1 до плоскости AB1D1.
Ответ: а) a;

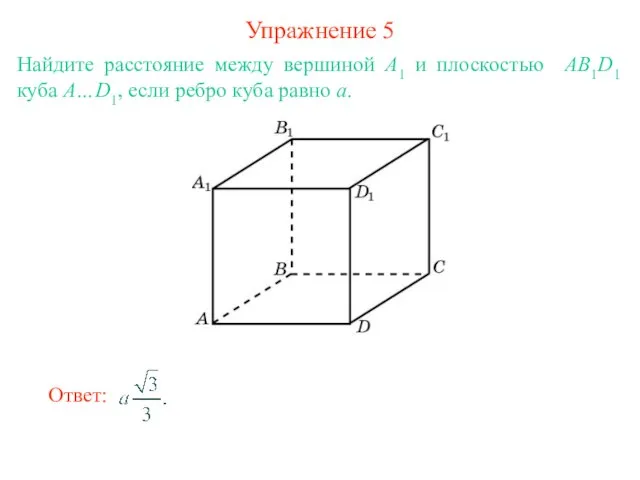
Упражнение 5
Найдите расстояние между вершиной A1 и плоскостью AB1D1 куба A…D1, если ребро куба равно a.

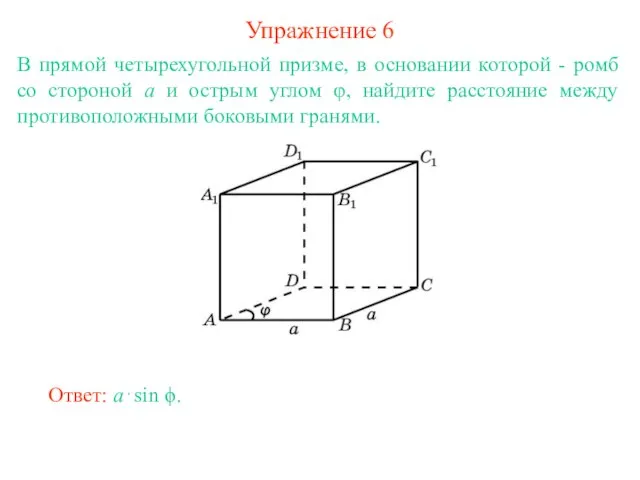
Упражнение 6
В прямой четырехугольной призме, в основании которой - ромб со стороной а и острым углом φ, найдите расстояние между противоположными боковыми гранями.
Ответ: a⋅sin ϕ.

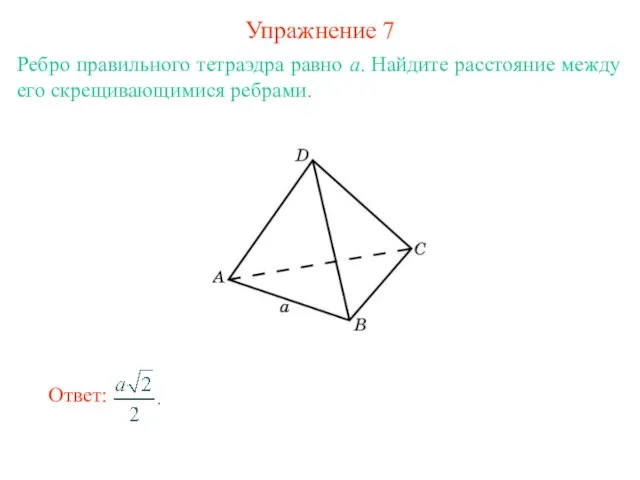
Упражнение 7
Ребро правильного тетраэдра равно a. Найдите расстояние между его скрещивающимися ребрами.

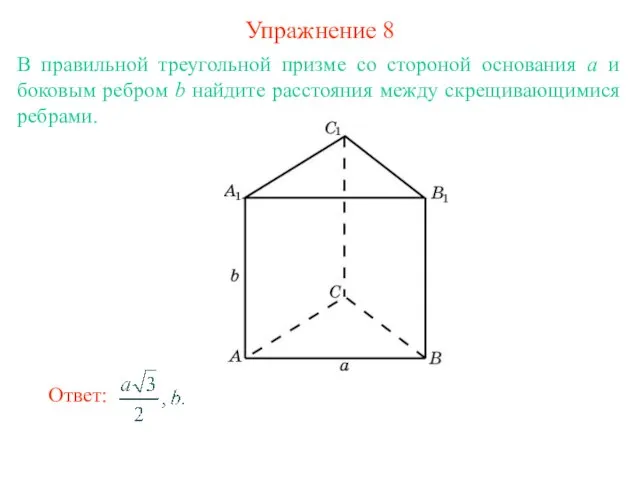
Упражнение 8
В правильной треугольной призме со стороной основания а и боковым ребром b найдите расстояния между скрещивающимися ребрами.

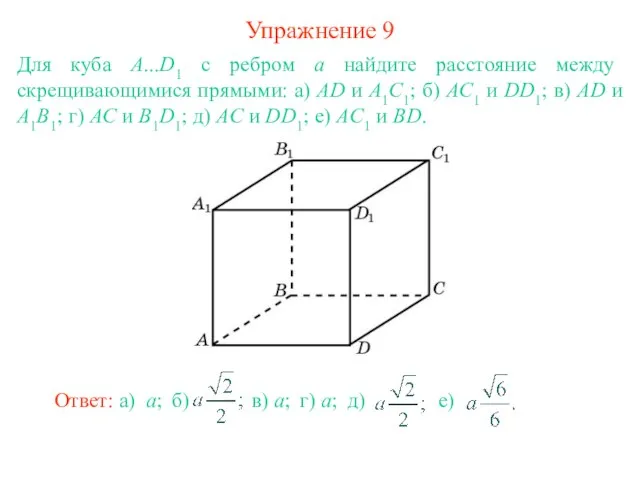
Упражнение 9
Для куба A...D1 с ребром а найдите расстояние между скрещивающимися прямыми: а) AD и A1C1; б) AC1 и DD1; в) AD и A1B1; г) AC и B1D1; д) AC и DD1; е) AC1 и BD.
Ответ: а) a;
в) a;
г) a;

Упражнение 10
Найдите геометрическое место точек пространства, равноудаленных от двух параллельных прямых.
Ответ: Плоскость.

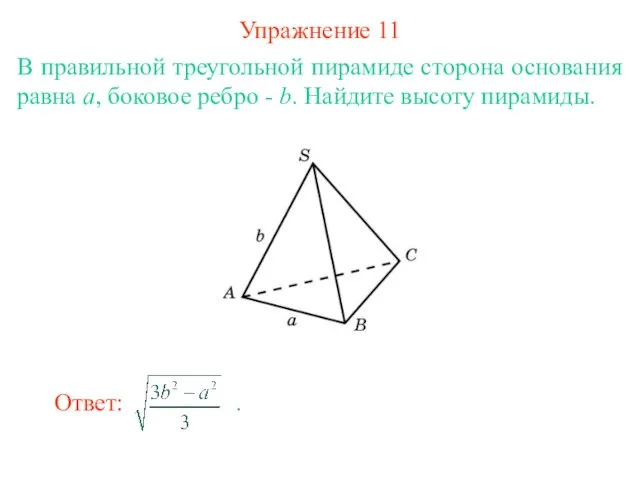
Упражнение 11
В правильной треугольной пирамиде сторона основания равна a, боковое ребро - b. Найдите высоту пирамиды.

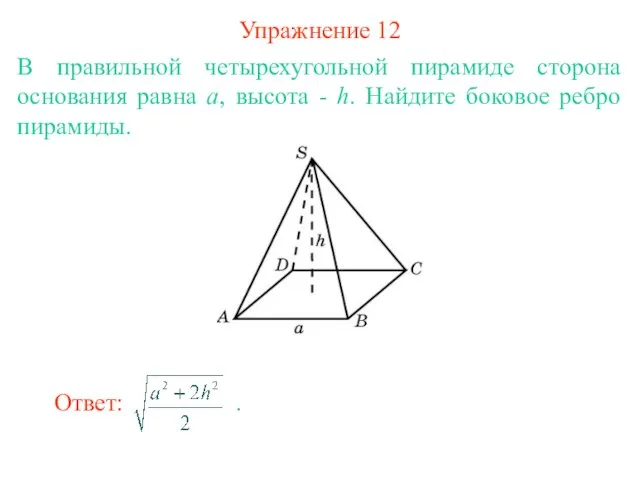
Упражнение 12
В правильной четырехугольной пирамиде сторона основания равна а, высота - h. Найдите боковое ребро пирамиды.

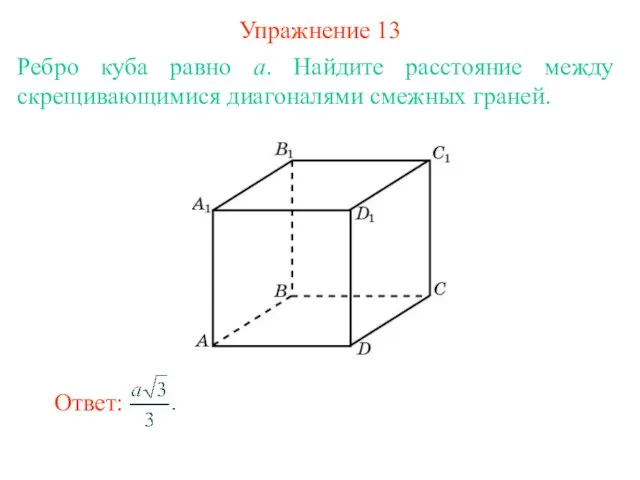
Упражнение 13
Ребро куба равно a. Найдите расстояние между скрещивающимися диагоналями смежных граней.