Содержание
- 2. С о д е р ж а н и е Из истории математики Определения Некоторые свойства
- 3. Из истории математики Прямоугольный треугольник занимает почётное место в вавилонской геометрии, упоминание о нём часто встречается
- 4. Определения Если один из углов треугольника прямой, то треугольник называется прямоугольным. А В С Сторона прямоугольного
- 5. Некоторые свойства прямоугольных треугольников 1. Сумма двух острых углов прямоугольного треугольника равна 900. 2. Катет прямоугольного
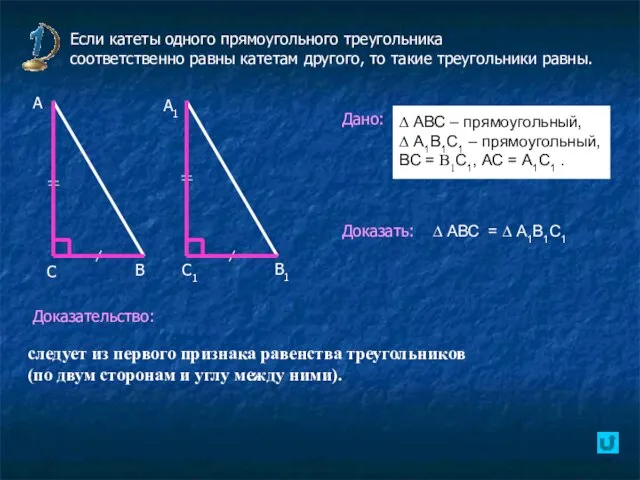
- 6. Признаки равенства прямоугольных треугольников Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники
- 7. Признаки равенства прямоугольных треугольников Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники
- 8. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. Дано: Доказать: Доказательство:
- 9. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему
- 10. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то
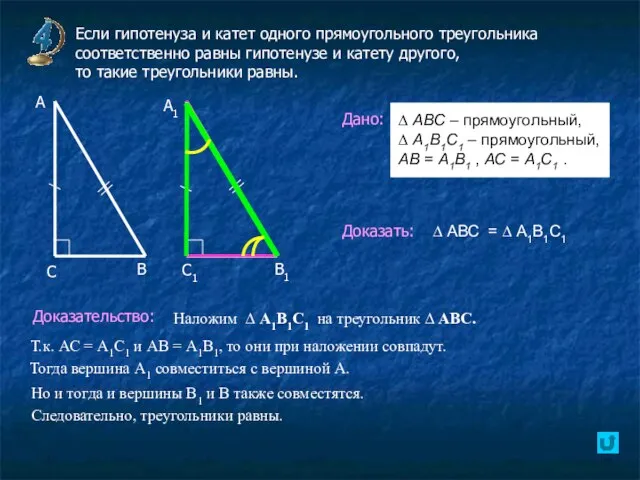
- 11. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники
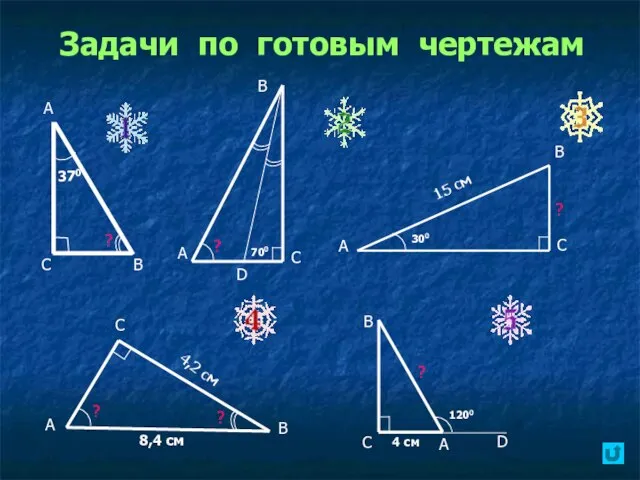
- 12. Задачи по готовым чертежам А С В D ? В А С 370 ? ? А
- 13. Контрольный тест 1. Прямоугольным называется треугольник, у которого а) все углы прямые; б) два угла прямые;
- 14. 2. В прямоугольном треугольнике всегда а) два угла острых и один прямой; б) один острый угол,
- 15. 3. Стороны прямоугольного треугольника, образующие прямой угол, называются а) сторонами треугольника; б) катетами треугольника; в) гипотенузами
- 16. 4. Сторона прямоугольного треугольника, противолежащая прямому углу, называется а) стороной треугольника; б) катетом треугольника; в) гипотенузой
- 17. Контрольный тест
- 18. Об авторе Данная разработка выполнена учителем математики МОУ «Средняя общеобразовательная школа № 33» г.Брянска Кулешовой Галиной
- 19. Папирус Ахмеса Математический папирус Ахмеса — древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства,
- 20. Е В К Л И Д Евклид (Eνκλειδηζ), древнегреческий математик, автор первого из дошедших до нас
- 21. Это интересно Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто
- 22. Ответ не правильный. Более внимательно изучи данную тему!
- 23. Вы верно ответили на все вопросы !
- 25. Скачать презентацию



















 Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Взаимное положение прямых Начертательная геометрия 11 класс
Взаимное положение прямых Начертательная геометрия 11 класс Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Осевая и центральная симметрии
Осевая и центральная симметрии Проецирование (8 класс)
Проецирование (8 класс) Теорема Пифагора. Приминение
Теорема Пифагора. Приминение Длина отрезка
Длина отрезка Окружность в аксонометрии
Окружность в аксонометрии Сечения
Сечения Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Перпендикулярные прямые на плоскости
Перпендикулярные прямые на плоскости Круги Эйлера и их практическое применение
Круги Эйлера и их практическое применение Длина окружности. Площадь круга
Длина окружности. Площадь круга Измерение углов
Измерение углов Теорема, обратная теореме Пифагора - презентация по Геометрии_
Теорема, обратная теореме Пифагора - презентация по Геометрии_ Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника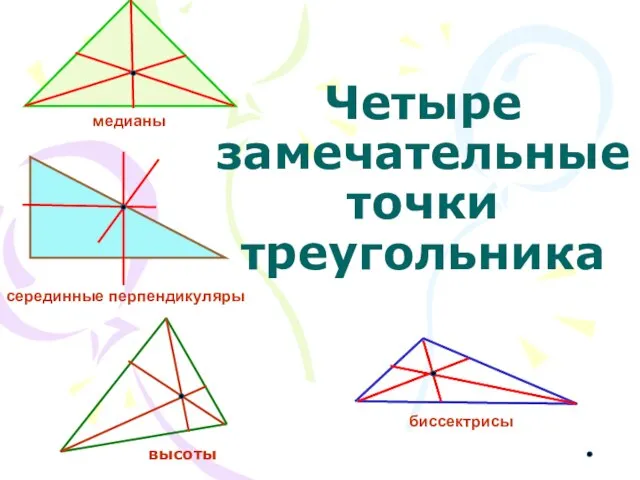 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Учитель Лемешкина А.М.
Учитель Лемешкина А.М.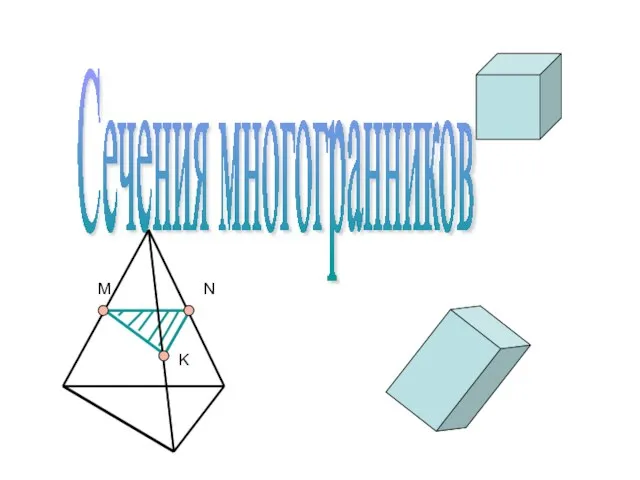 Сечения многогранников
Сечения многогранников УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА"
УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА" Тест по теме: «Площади многоугольников»
Тест по теме: «Площади многоугольников»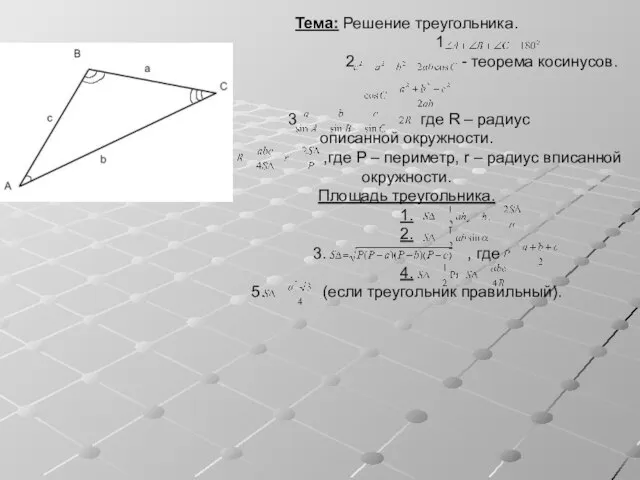 Решение треугольника
Решение треугольника Приготовьтесь к построению!
Приготовьтесь к построению! Равнобедренный треугольник
Равнобедренный треугольник Фракталы и их применение в наши дни
Фракталы и их применение в наши дни Прямоугольный параллелепипед
Прямоугольный параллелепипед Площади
Площади