Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья
Содержание
- 2. Cодержание
- 3. Введение В элементарной математике, самыми трудными считаются геометрические задачи. При решении геометрических задач, как правило, алгоритмов
- 4. Свойство Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться. Доказательство:
- 5. Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на
- 6. Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.
- 7. Отношение площадей подобных треугольников равны квадрату коэффициента подобия. Свойство Доказательство: Рассмотрим ∆ABC и ∆MBN. Пусть AB
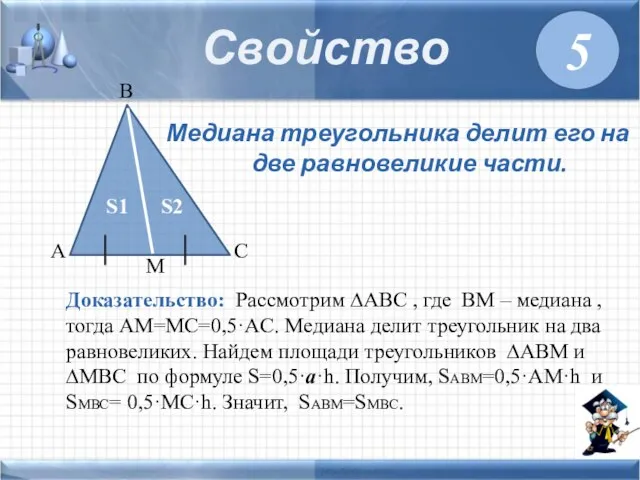
- 8. Медиана треугольника делит его на две равновеликие части. Свойство Доказательство: Рассмотрим ∆ABC , где BM –
- 9. Медианы треугольника делят его на три равновеликие части. Свойство Доказательство: Рассмотрим ∆ABC. Проведем медианы из всех
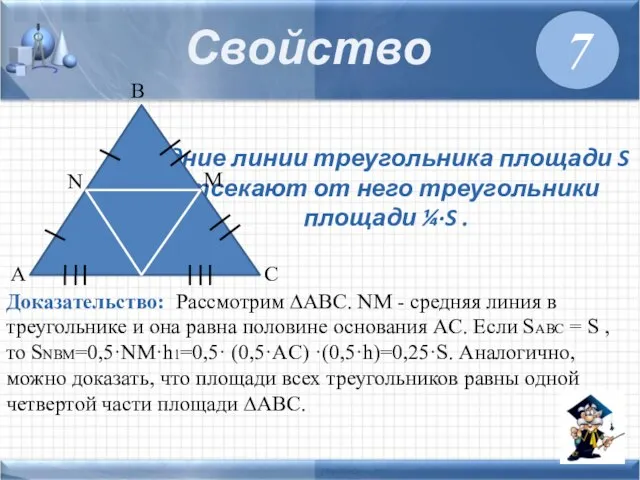
- 10. Средние линии треугольника площади S отсекают от него треугольники площади ¼·S . Свойство Доказательство: Рассмотрим ∆ABC.
- 11. Медианы треугольника делят его на 6 равновеликих частей. Свойство Доказательство: По свойству №7 площади ∆AOB, ∆BOC,
- 12. Утверждение 1 Два треугольника являются равновеликими, если равны их высоты и основания. Задача 1. Докажите, что
- 13. Задача 2. На стороне CD параллелограмма ABCD взята произвольная точка Е. Зная, что S∆ABE = S,
- 14. Задача 3. В параллелограмме ABCD на сторонах AB и CD взяты произвольные точки M и N.
- 15. Утверждение 2. Медиана треугольника делит его на два равновеликих треугольника. Задача 4. В параллелограмме ABCD точка
- 16. Задача 5. Докажите, что диагонали параллелограмма делят его на четыре равновеликих треугольника. Решение. В силу задачи
- 17. Задача 6. На продолжении стороны треугольника АВС взята точка D так, что АС = СD. Пусть
- 18. Задача типа С4 на ЕГЭ Медиана BM ∆ABC равна его высоте AH. Найдите угол MBC. Решение.
- 20. Скачать презентацию















 Двугранные углы
Двугранные углы Тема урока: УГОЛ Цель урока: сформировать полное представление о угле как геометрическом понятии
Тема урока: УГОЛ Цель урока: сформировать полное представление о угле как геометрическом понятии Прямоугольные треугольники
Прямоугольные треугольники Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Неевклидова геометрия
Неевклидова геометрия Сравнение величин углов. Классификация углов по градусной мере
Сравнение величин углов. Классификация углов по градусной мере Задача, приводимая к понятию "производная"
Задача, приводимая к понятию "производная" Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника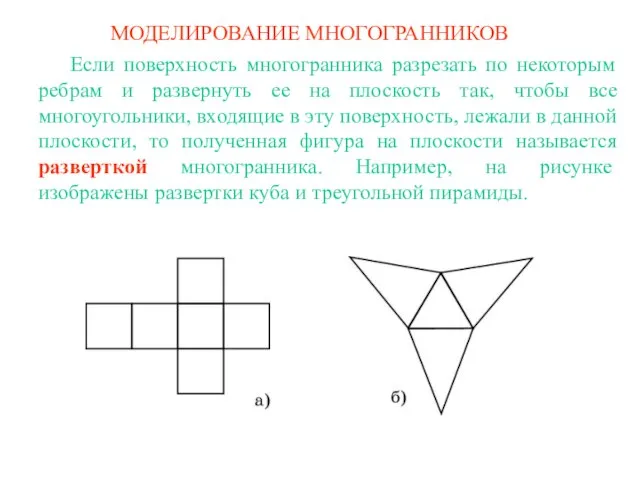 Моделирование многогранников
Моделирование многогранников Осевая и центральная симметрии
Осевая и центральная симметрии Преобразование плоскости
Преобразование плоскости Окружность и круг
Окружность и круг Длина окружности
Длина окружности Вводное повторение курса геометрии
Вводное повторение курса геометрии Расстояние от точки до прямой
Расстояние от точки до прямой Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве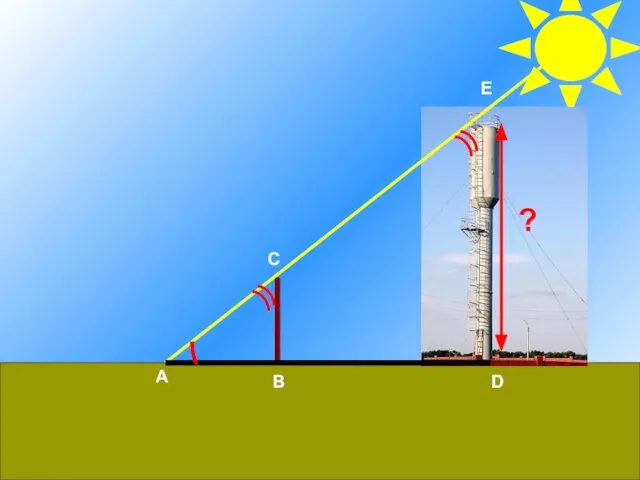 Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников Теорема Пифагора. Приминение
Теорема Пифагора. Приминение Симметрия
Симметрия Теорема Пифагора 7-9 класс
Теорема Пифагора 7-9 класс Презентация на тему: Параллельный перенос
Презентация на тему: Параллельный перенос Признаки равенства треугольников
Признаки равенства треугольников Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Положение плоскости относительно плоскостей проекций
Положение плоскости относительно плоскостей проекций