Вневписанная окружность

Содержание
Введение.
Основная часть
Глава 1. Определение вневписанной окружности.
Центр вневписанной окружности. Касательная к вневписанной окружности.
Глава 2. Формулы для вычисления радиусов вневписанных
окружностей.
§ 1. Соотношение между радиусом вневписанной окружности и
периметром треугольника
§ 2. Соотношение между радиусом вневписанной окружности, площадью и
периметром треугольника
Глава 3. Некоторые соотношения с радиусами вневписанных
окружностей.
§ 1. Выражение суммы радиусов вневписанных окружностей через
радиус вписанной окружности и радиус описанной окружности
§ 2. Выражение суммы величин, обратных радиусам вневписанных
окружностей, через величину обратную радиусу вписанных
окружностей.
§ 3. Выражение суммы всех попарных произведений радиусов
вневписанных окружностей через квадрат полупериметра
треугольника.
§ 4. Выражение произведения радиусов вневписанных окружностей
через произведение радиуса вписанной окружности и
квадрат полупериметра треугольника.
§ 5. Выражение высоты треугольника через радиусы вневписанных
окружностей.
Заключение.
Библиография.

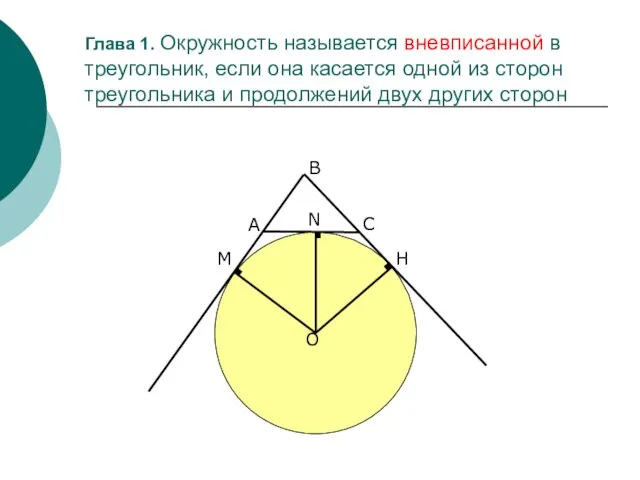
Глава 1. Окружность называется вневписанной в треугольник, если она касается одной из сторон треугольника и продолжений двух других сторон
М
N
H

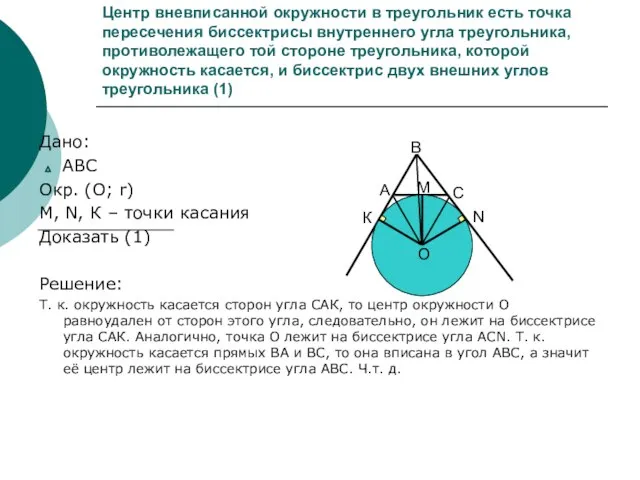
Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника (1)
Дано:
АВС
Окр. (О; r)
М, N, К – точки касания
Доказать (1)
Решение:
Т. к. окружность касается сторон угла САК, то центр окружности О равноудален от сторон этого угла, следовательно, он лежит на биссектрисе угла САК. Аналогично, точка О лежит на биссектрисе угла АСN. Т. к. окружность касается прямых ВА и ВС, то она вписана в угол АВС, а значит её центр лежит на биссектрисе угла АВС. Ч.т. д.

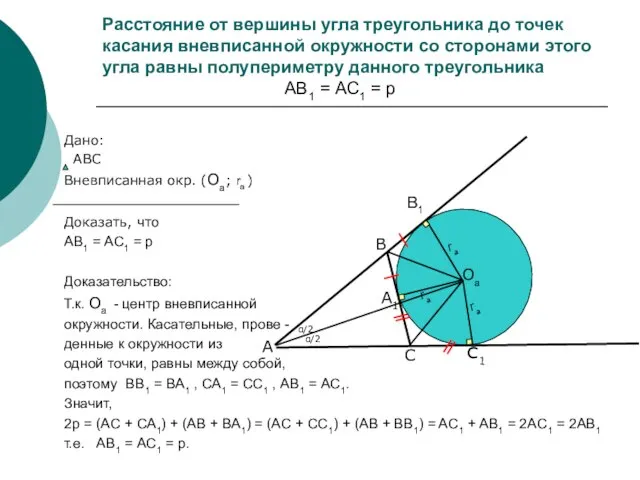
Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника
АВ1 = АС1 = p
Дано:
АВС
Вневписанная окр. (Оа; ra )
Доказать, что
АВ1 = АС1 = p
Доказательство:
Т.к. Оа - центр вневписанной
окружности. Касательные, прове -
денные к окружности из
одной точки, равны между собой,
поэтому ВВ1 = ВА1 , СА1 = СС1 , АВ1 = АС1.
Значит,
2p = (AC + СА1) + (AB + ВА1) = (AC + CC1) + (AB + BB1) = AC1 + AB1 = 2AC1 = 2AB1
т.е. АВ1 = АС1 = p.
Оа
В1
ra
ra
ra
А
В
С
С1
А1
α/2
α/2

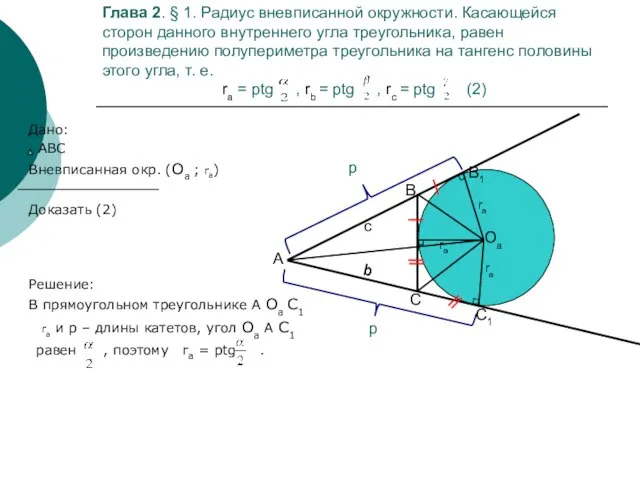
Глава 2. § 1. Радиус вневписанной окружности. Касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е.
ra = ptg , rb = ptg , rc = ptg (2)
Дано:
АВС
Вневписанная окр. (Оа ; ra)
Доказать (2)
Решение:
В прямоугольном треугольнике А Оа С1
ra и p – длины катетов, угол Оа А С1
равен , поэтому ra = ptg .
А
В
С
Оа
p
p
В1
С1
b
c
ra
ra
ra

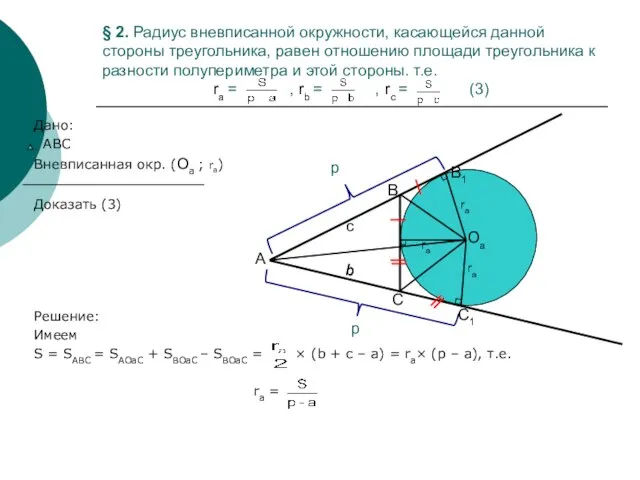
§ 2. Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны. т.е.
ra = , rb = , rc = (3)
Дано:
АВС
Вневписанная окр. (Оа ; ra)
Доказать (3)
Решение:
Имеем
S = SABC = SAOaC + SBOaC – SBOaC = × (b + c – a) = ra× (p – a), т.е.
ra =
А
В
С
Оа
p
p
В1
С1
b
c
ra
ra
ra

Глава 3. § 1 Сумма радиусов вневписанных окружностей равна сумме радиуса вписанной окружности и удвоенного диаметра описанной окружности, т. е.
ra + rb + rc = r + 4R
Доказательство:
Выразим все радиусы через стороны, площадь и полупериметр треугольника:
r = , R = , ra = , rb = , rc =
Значит,
ra + rb + rc – r = + + - =
= =
= = = 4R

§ 2. Сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, т. е.
Доказательство:
Используем выражения радиусов через стороны и площадь треугольника:
r = , R = , ra = , rb = , rc =
Значит,

§ 3. Сумма всех попарных произведений радиусов вневписанных окружностей равна квадрату полупериметра треугольника, т. е.
rarb + rbrc + rcra = p2
Доказательство:
Воспользуемся формулами ранее доказанных радиусов через стороны и площадь треугольника:
r = , ra = , rb = , rc =
Подставим
Из формулы Герона следует
(p – a)(p – b)(p – c) = , поэтому

§ 4. Произведение всех трех радиусов вневписанных окружностей равно произведению радиуса вписанной окружности на квадрат полупериметра треугольника, т.е.
rarbrc = rp2
Доказательство:
Из ранее доказанных формул для радиусов и формулы Герона
ra = , rb = , rc = ,
Тогда

Следствие 1. Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е.
Доказательство:
Из rarbrc = rp2 = rp × p = Sp.
Следовательно

Следствие 2. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности, т.е.
Доказательство:
Из следствия 1, что и равенства S = pr,
получаем, перемножая их почленно,
. Значит

§ 5. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам вневписанных окружностей, касающихся двух других сторон треугольника, т.е.
, ,
Доказательство:
Воспользуемся формулами
,
Значит,
,