Слайд 2Взаимное расположение двух прямых
Как могут располагаться две прямые в пространстве?
Прямые линии в

пространстве могут быть параллельными, пересекающимися и скрещивающимися.
Слайд 3Параллельные прямые
Параллельными называются две прямые, которые лежат в одной плоскости и
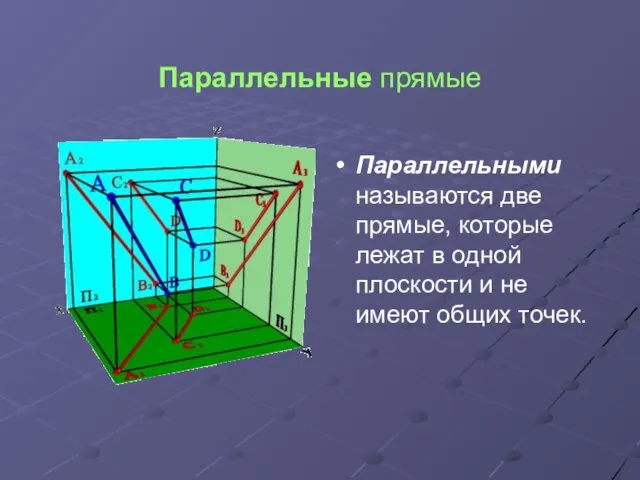
не имеют общих точек.
Слайд 4Параллельные прямые
Проекции параллельных прямых - параллельны.
Если AB//CD то A1B1//C1D1; A2B2//C2D2;
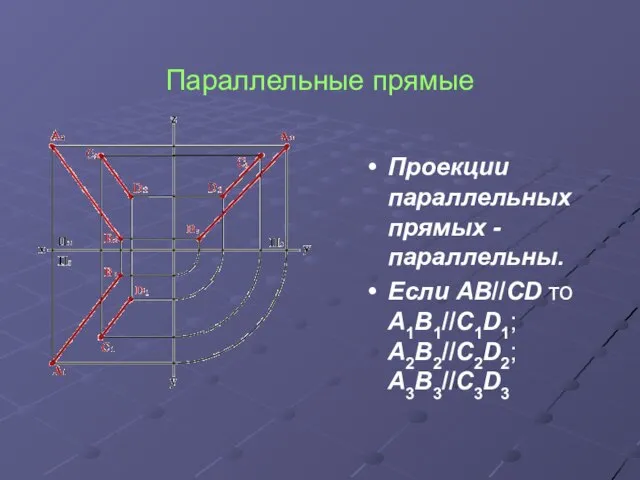
A3B3//C3D3
Слайд 5Профильные прямые
Особый случай представляют собой прямые, параллельные одной из плоскостей проекций.
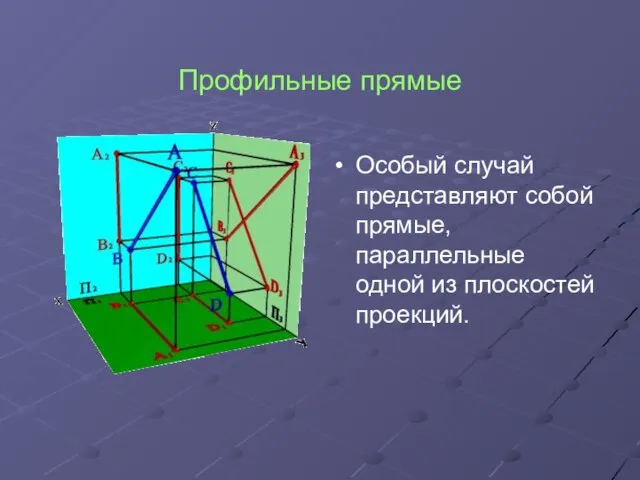
Слайд 6Профильные прямые
Если фронтальные и горизонтальные проекции профильных прямых параллельны, то для оценки

их взаимного положения необходимо сделать проекцию на профильную плоскость.
Слайд 7Профильные прямые
В рассмотренном случае проекции отрезков на плоскости П3 пересекаются, следовательно, прямые
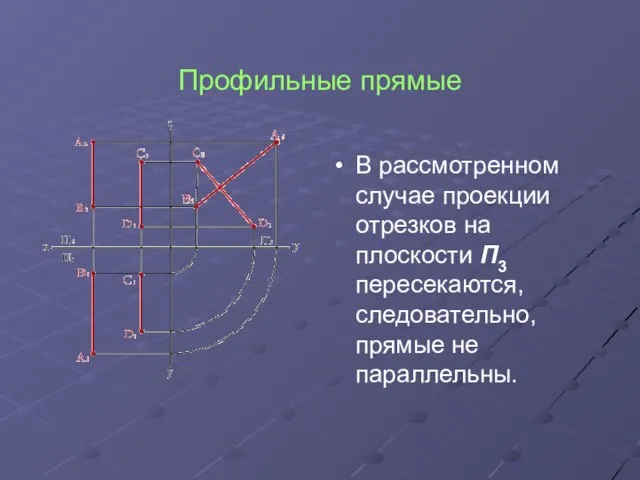
не параллельны.
Слайд 8Пересекающиеся прямые
Пересекающимися называются две прямые лежащие в одной плоскости и имеющие
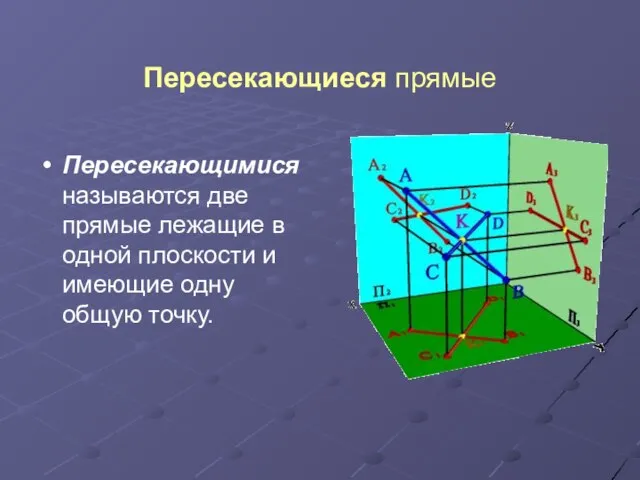
одну общую точку.
Слайд 9Пересекающиеся прямые
Если прямые пересекаются, то точки пересечения их одноименных проекций находится на

одной линии связи
Слайд 10Пересекающиеся прямые?
Если одна из прямых параллельна какой-либо из плоскостей проекций, по двум
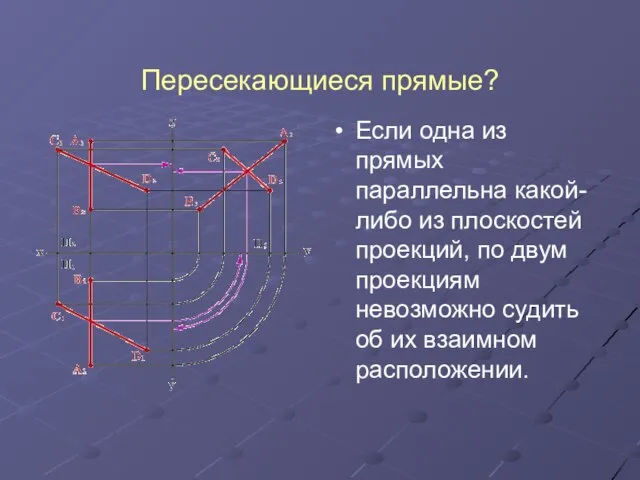
проекциям невозможно судить об их взаимном расположении.
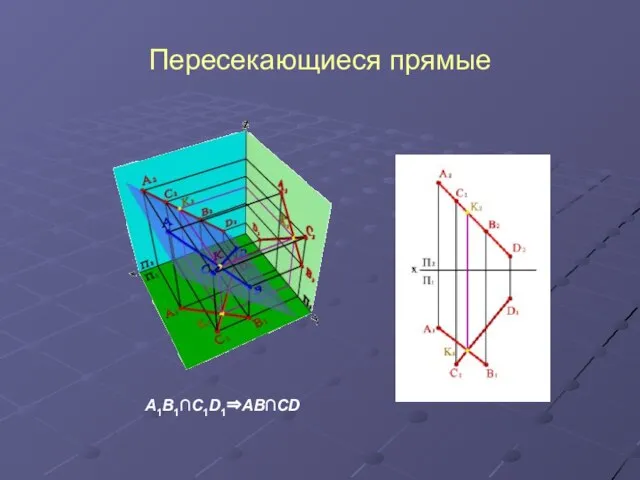
Слайд 11Пересекающиеся прямые
А1В1∩С1D1⇒АВ∩СD
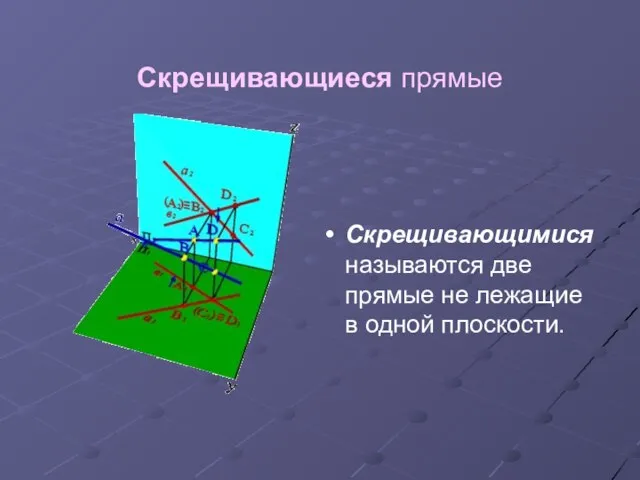
Слайд 12Скрещивающиеся прямые
Скрещивающимися называются две прямые не лежащие в одной плоскости.
Слайд 13Скрещивающиеся прямые
Если прямые не пересекаются и не параллельны между собой, то точка

пересечения их одноименных проекций не лежит на одной линии связи.
Слайд 14Способ определения видимости
по конкурентным точкам
В данном случае точки А и В-
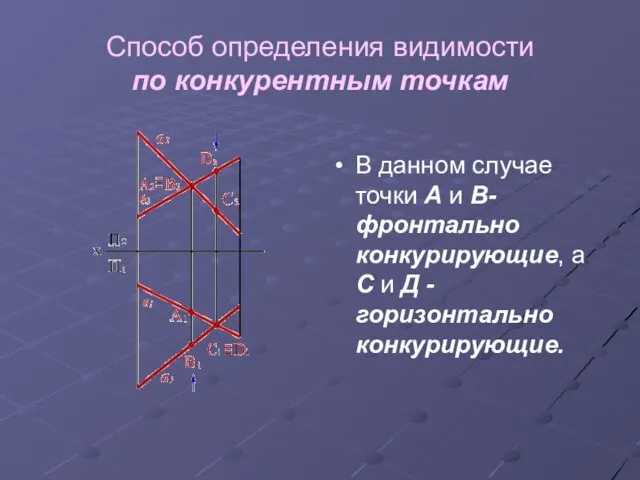
фронтально конкурирующие, а С и Д -горизонтально конкурирующие.













 Что такое геометрия
Что такое геометрия ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ Лабораторный практикум по геометрии 7 класс
Лабораторный практикум по геометрии 7 класс Геометрия. Как она возникла?
Геометрия. Как она возникла?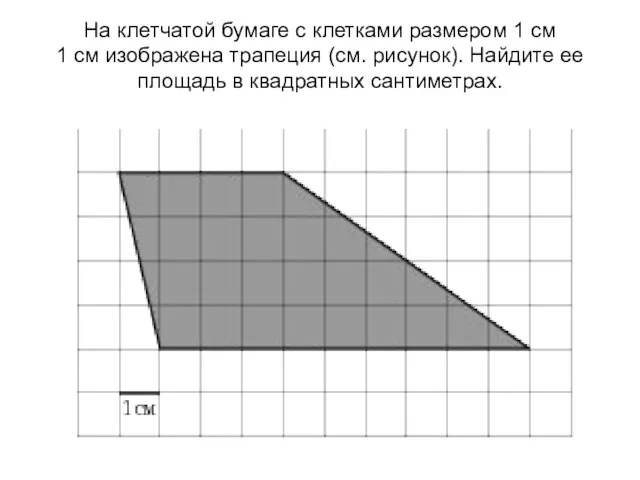 Площади фигур на клетке
Площади фигур на клетке Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Стереометрия в образах
Стереометрия в образах Многообразие многоугольников
Многообразие многоугольников Геометрические задачи «С2» - презентация по Геометрии_
Геометрические задачи «С2» - презентация по Геометрии_ Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ Площадь квадрата, прямоугольника, параллелограмма - презентация по Геометрии_
Площадь квадрата, прямоугольника, параллелограмма - презентация по Геометрии_ Бозон Хиддинса
Бозон Хиддинса Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Площадь многоугольника 8 класс
Площадь многоугольника 8 класс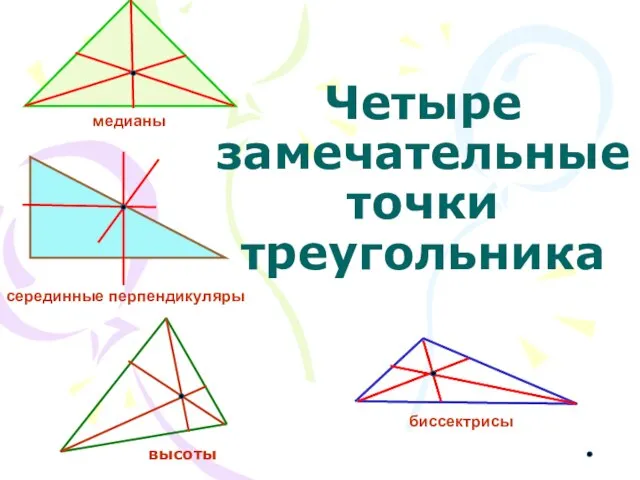 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника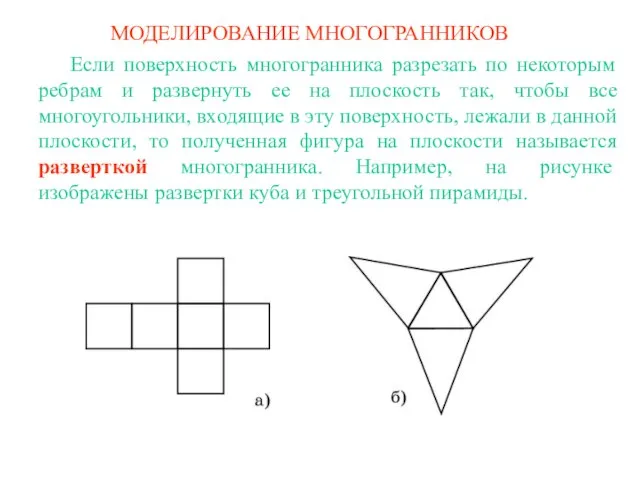 Моделирование многогранников
Моделирование многогранников Площадь прямоугольного треугольника
Площадь прямоугольного треугольника Логарифм. Основные понятия
Логарифм. Основные понятия Расстояние от точки до прямой
Расстояние от точки до прямой Объём пирамиды
Объём пирамиды тренажёр по теме смежные и вертикальные углы
тренажёр по теме смежные и вертикальные углы Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Тригонометрические неравенства
Тригонометрические неравенства Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Параллелепипед
Параллелепипед