Содержание
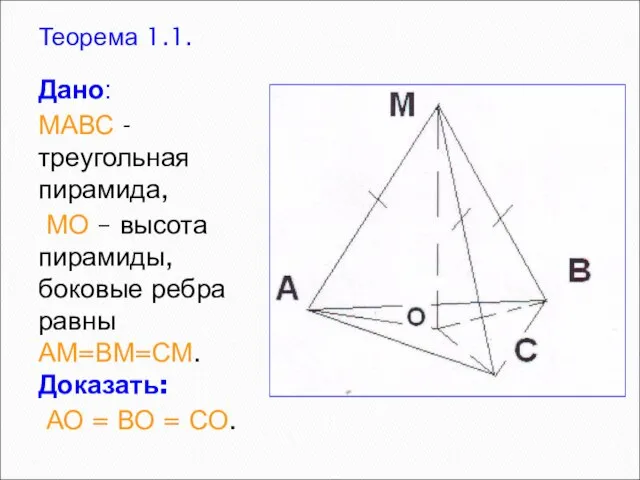
- 2. Теорема 1.1. Дано: МАВС - треугольная пирамида, МО – высота пирамиды, боковые ребра равны АМ=ВМ=СМ. Доказать:
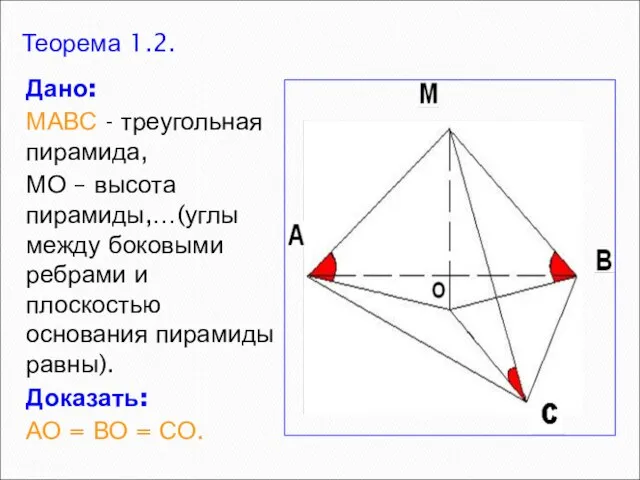
- 3. Теорема 1.2. Дано: МАВС - треугольная пирамида, МО – высота пирамиды,…(углы между боковыми ребрами и плоскостью
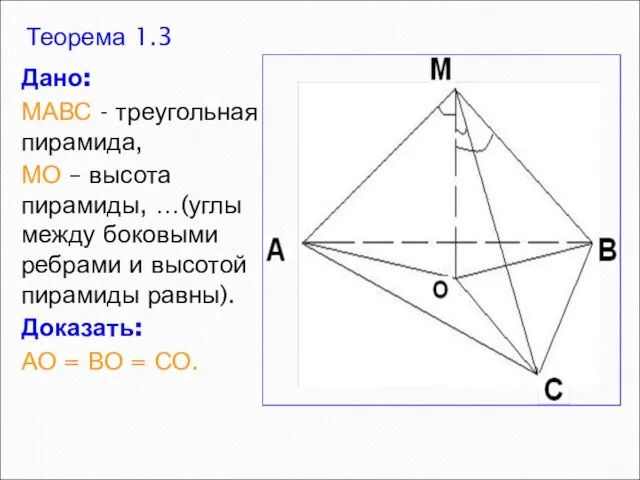
- 4. Теорема 1.3 Дано: МАВС - треугольная пирамида, МО – высота пирамиды, …(углы между боковыми ребрами и
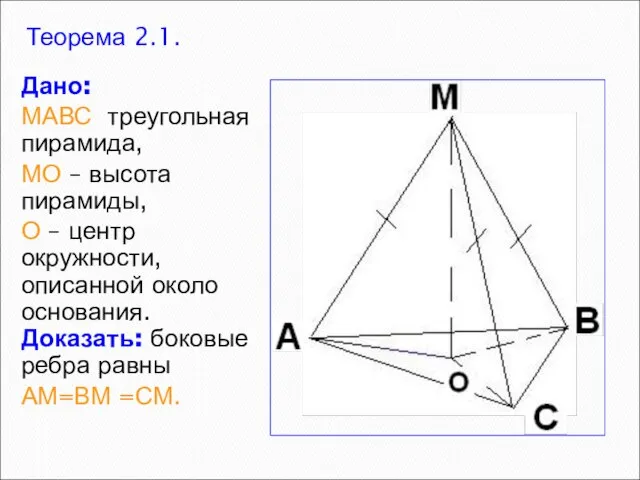
- 5. Теорема 2.1. Дано: МАВС треугольная пирамида, МО – высота пирамиды, О – центр окружности, описанной около
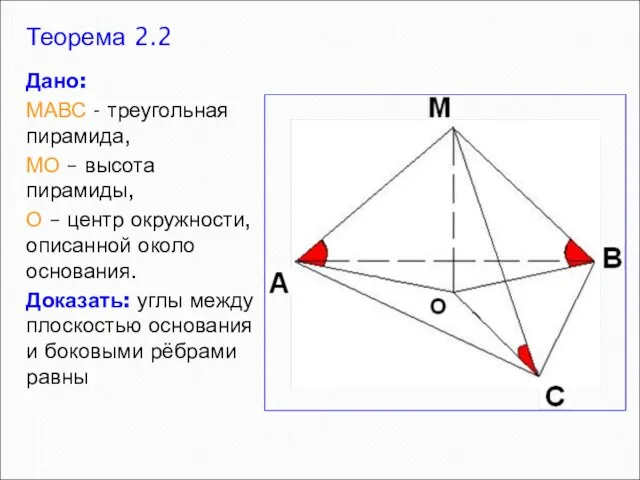
- 6. Теорема 2.2 Дано: МАВС - треугольная пирамида, МО – высота пирамиды, О – центр окружности, описанной
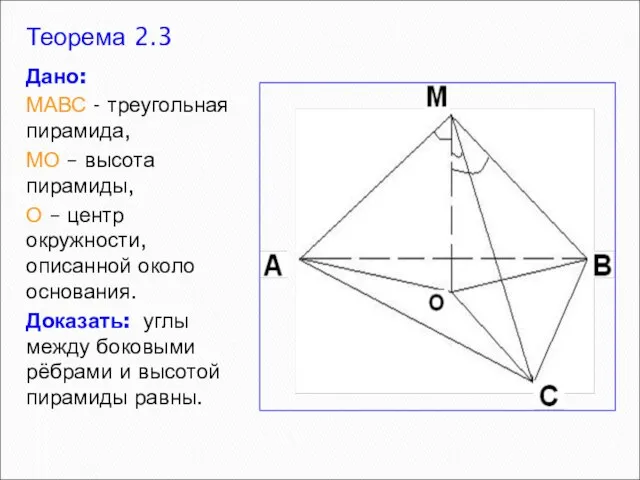
- 7. Теорема 2.3 Дано: МАВС - треугольная пирамида, МО – высота пирамиды, О – центр окружности, описанной
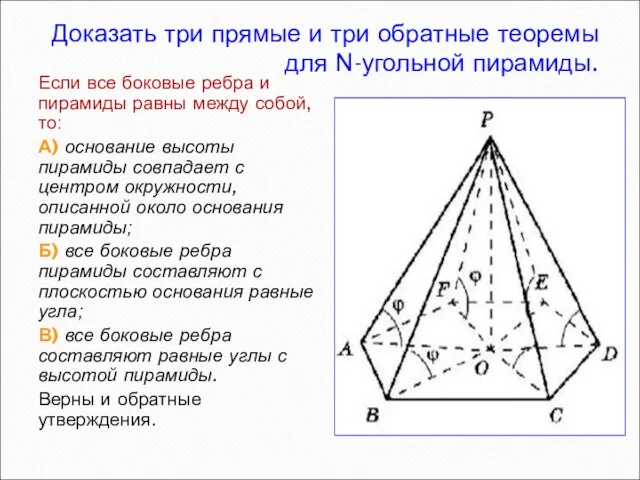
- 8. Доказать три прямые и три обратные теоремы для N-угольной пирамиды. Если все боковые ребра и пирамиды
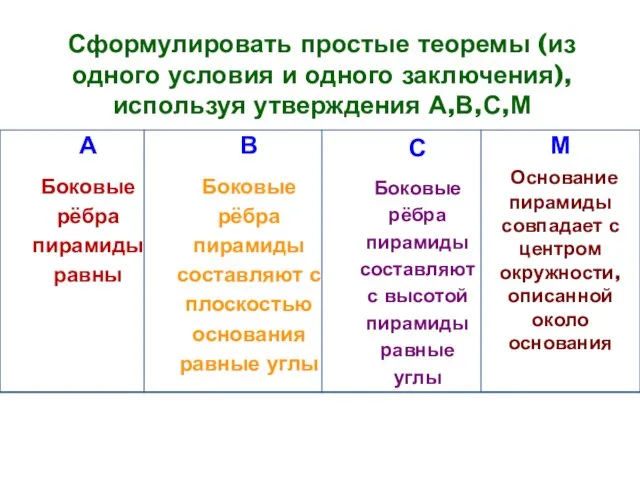
- 9. Сформулировать простые теоремы (из одного условия и одного заключения), используя утверждения А,В,С,М
- 10. Алгоритм решения 2-х шаговых задач
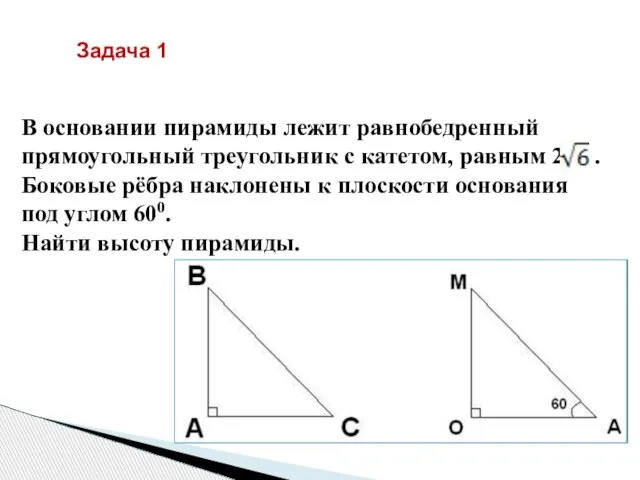
- 11. В основании пирамиды лежит равнобедренный прямоугольный треугольник с катетом, равным 2 . Боковые рёбра наклонены к
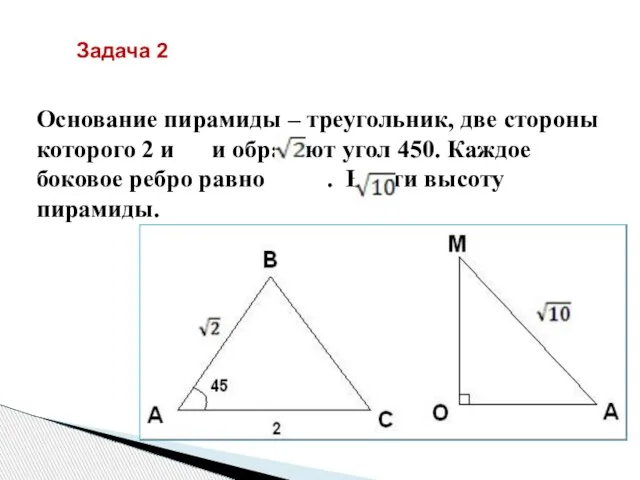
- 12. Основание пирамиды – треугольник, две стороны которого 2 и и образуют угол 450. Каждое боковое ребро
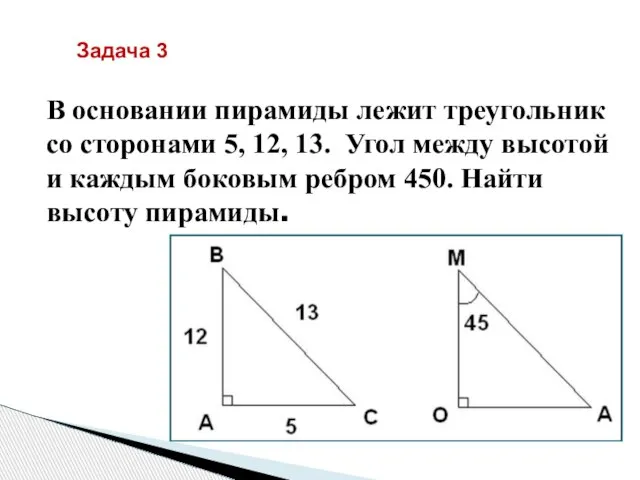
- 13. В основании пирамиды лежит треугольник со сторонами 5, 12, 13. Угол между высотой и каждым боковым
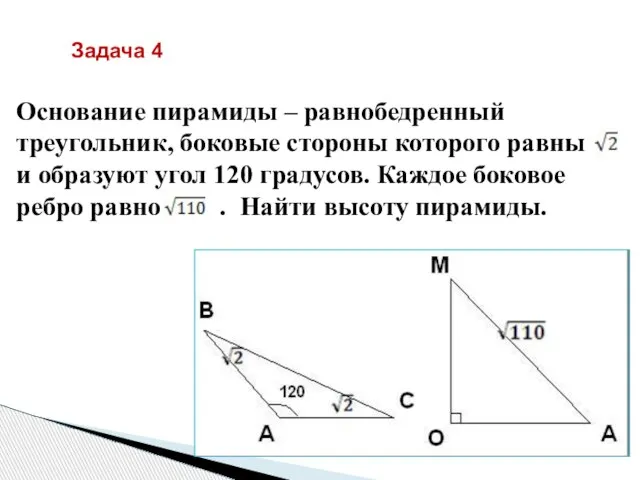
- 14. Основание пирамиды – равнобедренный треугольник, боковые стороны которого равны и образуют угол 120 градусов. Каждое боковое
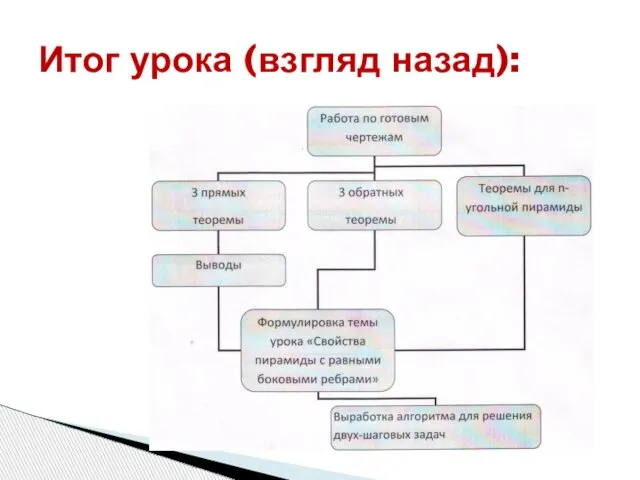
- 15. Итог урока (взгляд назад):
- 17. Скачать презентацию

 ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Треугольник Устные задачи
Треугольник Устные задачи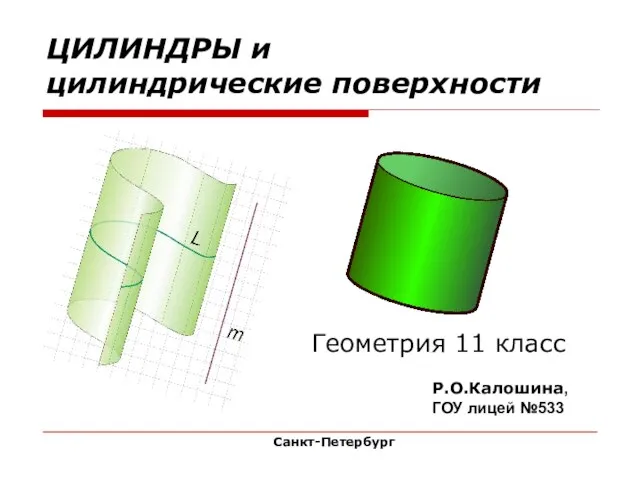 ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Параллелограмм
Параллелограмм Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Двумерный симплекс история его изучения
Двумерный симплекс история его изучения Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Сопряжение. Геометрические построения - презентация по Геометрии_
Сопряжение. Геометрические построения - презентация по Геометрии_ Симметрия. Осевая и центральная симметрии
Симметрия. Осевая и центральная симметрии Положение плоскости относительно плоскостей проекций
Положение плоскости относительно плоскостей проекций Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Правильная пирамида
Правильная пирамида Что такое окружность? - презентация по Геометрии_
Что такое окружность? - презентация по Геометрии_ Задания на клетчатой бумаге
Задания на клетчатой бумаге Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Амидекстр
Амидекстр Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Геометрия Лобачевского
Геометрия Лобачевского Геометрические задачи на экстремум
Геометрические задачи на экстремум Биссектриса угла
Биссектриса угла Что изучает геометрия 7 класс
Что изучает геометрия 7 класс Пирамиды
Пирамиды Объем наклонной призмы, пирамиды и конуса
Объем наклонной призмы, пирамиды и конуса Понятие цилиндра
Понятие цилиндра Перпендикуляр и наклонная
Перпендикуляр и наклонная Лист Мёбиуса
Лист Мёбиуса Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости