Содержание
- 2. 2. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ И ЕЁ ПРИМЕНЕНИЕ В ПРИРОДЕ И ТЕХНИКЕ. 1. Показательная функция. 3. В биологии.
- 3. Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде всего показательные, открывают доступ ко многим исследованиям. Л.Эйлер.
- 4. Графики функции у=2х и у=(½)х График функции у=2х проходит через точку (0;1) и расположен выше оси
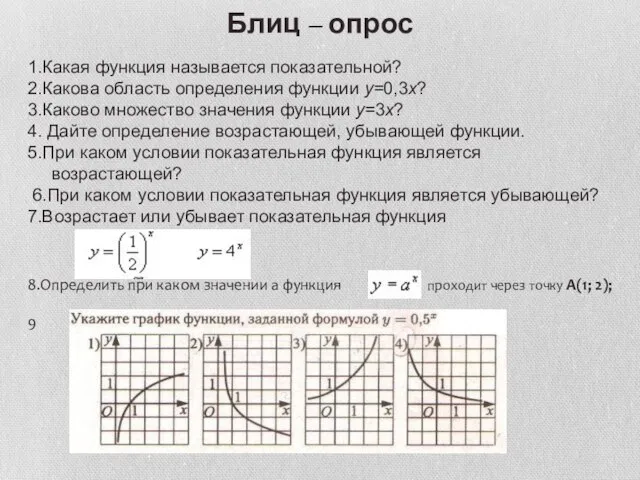
- 5. Блиц – опрос 1.Какая функция называется показательной? 2.Какова область определения функции y=0,3x? 3.Каково множество значения функции
- 6. Какие из перечисленных функций являются возрастающими, а какие убывающими?
- 7. Какие из функций являются возрастающими, а какие убывающими?
- 8. Показательные уравнения. Уравнения,у которых неизвестное находится в показателе степени, называются показательными. Способы решения: По свойству степени;
- 9. Решите уравнения ( устно): 5 х =25 х=2 7 х-2 =49 х=4 4 х =1 х
- 10. Указать способы решения показательных уравнений.
- 11. Диагностика уровня формирования практических навыков
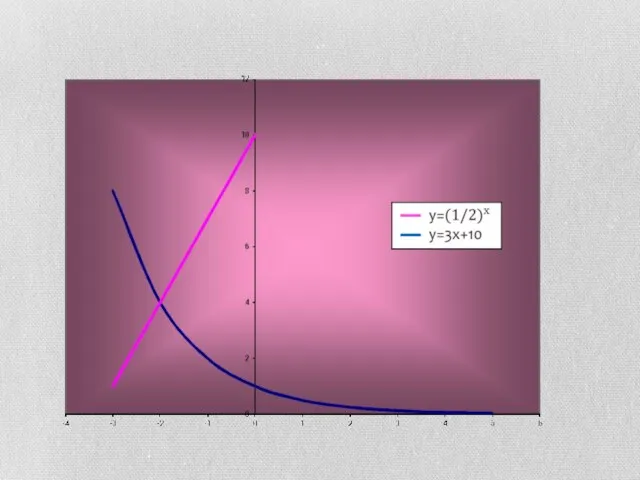
- 12. Чтобы решить графически уравнение f (x) = g (x) , надо: построить графики функций у =
- 14. Определение Показательные неравенства – это неравенства, в которых неизвестное содержится в показателе степени. Примеры:
- 15. Показательные неравенства решаются по следующим свойствам показательной функции: •если а > 1 , то неравенство a
- 16. Решите неравенства (устно): 2 х > 0 x- любое 2x >1 x > 0 х 1
- 17. Решения показательных неравенств: Способ Уравнивание оснований правой и левой части
- 18. Решите неравенство:
- 19. Решите неравенство:
- 20. Решение показательных неравенств Способ 2: Вынесение за скобки степени с меньшим показателем Ответ: х >3 3
- 21. Решение показательных неравенств Способ 3: введение новой переменной Ответ: х 0 3>1, то
- 22. И её применение в природе и технике. Показательная функция
- 23. Подумайте! Где может использоваться показательная функция? Тема «Показательная функция» является основополагающей при изучении таких тем, как
- 24. Наглядный бытовой пример! Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он
- 25. При падении тел в безвоздушном пространстве скорость их непрерывно возрастает. При падении тел в воздухе скорость
- 26. Рассмотрим задачу о падении парашютиста. Если считать, что сила сопротивления воздуха пропорциональна скорости падения парашютиста, т.е.
- 27. Много трудных математических задач приходится решать в теории межпланетных путешествий. Одной из них является задача об
- 28. Если не учитывать сопротивление воздуха и притяжение Земли, то масса топлива определиться формулой: M=m(ev/v0-1) (формула К.Э.Циалковского).
- 29. Если при колебаниях маятника, гири, качающейся на пружине, не пренебрегать сопротивлением воздуха, то амплитуда колебаний становится
- 30. Когда радиоактивное вещество распадется, его количество уменьшается. Через некоторое время остается половина первоначального количества вещества. Этот
- 31. Задача: Период полураспада плутония равен 140 суткам. Сколько плутония останется через 10 лет, если его начальная
- 32. Как видите, во всех приведенных выше исследованиях использовалась показательная функция.
- 33. Вот некоторые из Нобелевских лауреатов, получивших премию за исследования в области физики с использованием показательной функции:
- 34. Она не перестаёт нас удивлять! Показательная функция также используется при решении некоторых задач судовождения, например, функцию
- 35. Применение показательной функции в биологии .
- 36. Применение логарифмической функции в биологии. В питательной среде бактерия кишечной палочки делится каждую минуту. Понятно, что
- 37. Применение показательной функции в экономике
- 38. Задача: Ежемесячно на банковский вклад, равный S0 рублей начисляется р%. На сколько процентов возрастет банковский вклад
- 39. А теперь, в конце урока хочется, чтобы вы выразили свое отношение к нашей сегодняшней работе и
- 40. ДОМАШНЕЕ ЗАДАНИЕ Страница 57 учебника – «ПРОВЕРЬ СЕБЯ»
- 42. Скачать презентацию





































 Понятие многогранника
Понятие многогранника Путешествие в страну Геометрия
Путешествие в страну Геометрия Правильные многогранники
Правильные многогранники Цилиндр и конус
Цилиндр и конус Четырехугольники
Четырехугольники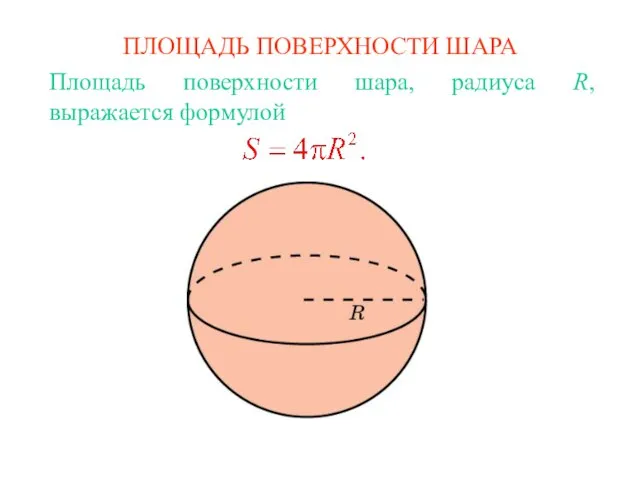 Площадь поверхности шара
Площадь поверхности шара Биссектриса угла
Биссектриса угла Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Параллельный перенос 11 класс - презентация_
Параллельный перенос 11 класс - презентация_ вид разреза сечения
вид разреза сечения Плоскость
Плоскость Понятие объема. Объем призмы
Понятие объема. Объем призмы Теоремы синусов и косинусов
Теоремы синусов и косинусов Стереометрия в образах
Стереометрия в образах Тетраэдр и параллепипед
Тетраэдр и параллепипед Решение треугольников. Измерительные работы на местности
Решение треугольников. Измерительные работы на местности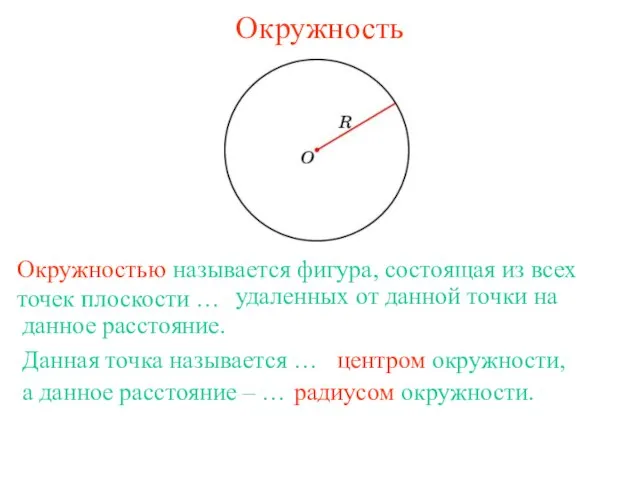 Окружность
Окружность Фракталы – геометрия природы
Фракталы – геометрия природы Многообразие многоугольников
Многообразие многоугольников Приготовьтесь к построению
Приготовьтесь к построению Окружность в аксонометрии
Окружность в аксонометрии Треугольники. Третий признак равенства
Треугольники. Третий признак равенства ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ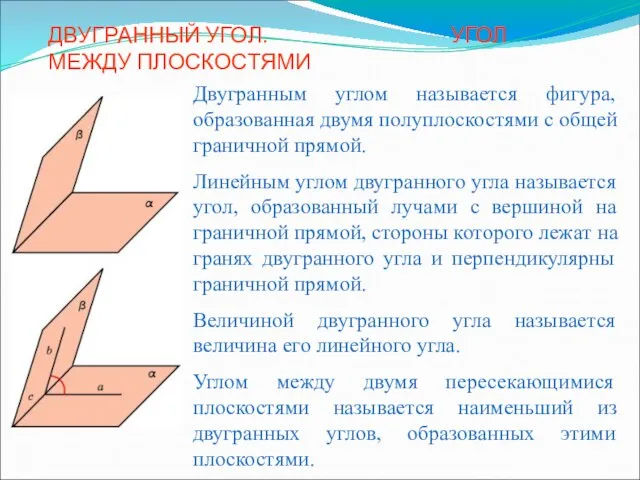 Двугранный угол. Угол между плоскостями4
Двугранный угол. Угол между плоскостями4 Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Урок повторения в 6 классе
Урок повторения в 6 классе В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Симметрия на планете Земля
Симметрия на планете Земля