ГИА 2013 Модуль «Геометрия» № 9

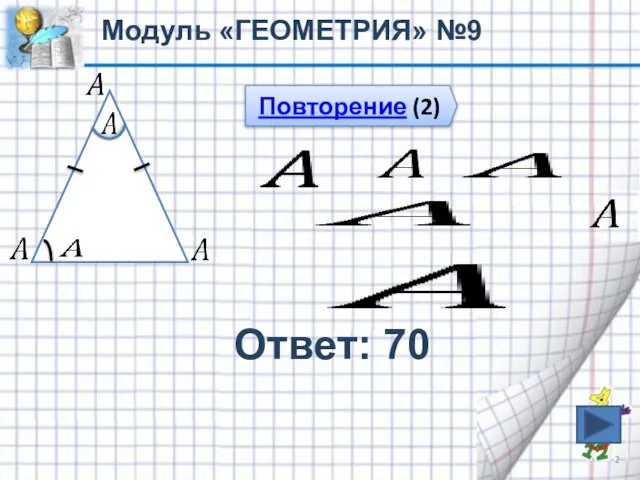
Модуль «ГЕОМЕТРИЯ» №9
Ответ: 70
Повторение (2)

Повторение
В равнобедренном треугольнике углы при основании равны
В треугольнике сумма углов равна 180°

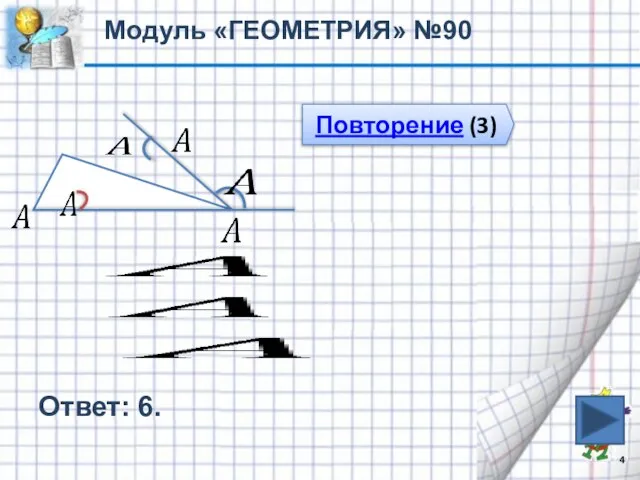
Ответ: 6.
Модуль «ГЕОМЕТРИЯ» №90
Повторение (3)

Повторение
Внешний угол треугольника – это угол, смежный с углом треугольника
Сумма смежных углов углов равна 180°
В треугольнике сумма углов равна 180°

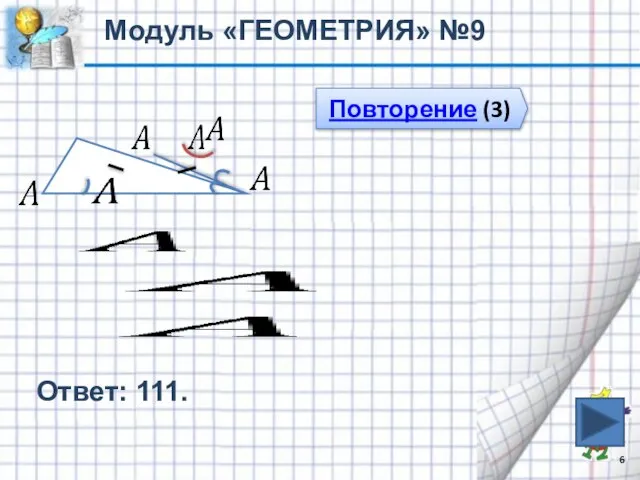
Ответ: 111.
Модуль «ГЕОМЕТРИЯ» №9
Повторение (3)

Повторение
В равнобедренном треугольнике углы при основании равны
Биссектриса – это луч, который делит угол пополам
В треугольнике сумма углов равна 180°

Найти наименьший из оставшихся углов ∆ АВС.
Модуль «ГЕОМЕТРИЯ» №9
Повторение
Наименьшим из оставшихся углов ∆ АВС является ∠В, так как третий угол равен 90°.
Ответ: 24.
∠В= 90°-66°=24°

Повторение
Сумма острых углов прямоугольного треугольника равна 90°

Ответ: 134.
Модуль «ГЕОМЕТРИЯ» №9
Один из углов параллелограмма на 46° больше другого. Найти больший из них.
Повторение (2)
∠А+∠D=180°
Пусть ∠А=х°, тогда∠D=х°+46°
х+х+46=180
2х=134
х=67
∠D =2∙67°=134°

Повторение
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны.
Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°

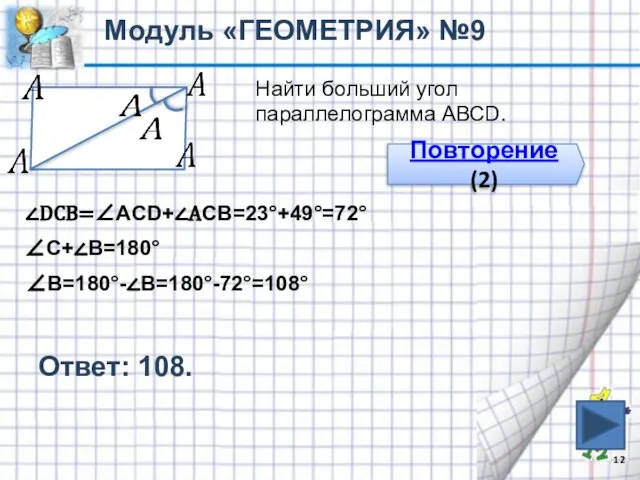
Ответ: 108.
Модуль «ГЕОМЕТРИЯ» №9
Найти больший угол параллелограмма АВСD.
Повторение (2)
∠DCВ=∠АCD+∠АСВ=23°+49°=72°
∠С+∠В=180°
∠В=180°-∠В=180°-72°=108°

Повторение
Если угол разделен на части, то его градусная мера равна сумме градусных мер его частей.
В параллелограмме сумма соседних углов равна 180°

Ответ: 90.
Модуль «ГЕОМЕТРИЯ» №9
АВСD параллелограмм.
Повторение (2)
Отрезок АС явл. диагональю параллелограмма.
Углы при вершине А равны, зн. углы при вершине С тоже равны.
⇒
АВСD - ромб.
АС ⊥ BD, зн. Угол, под которым пересекаются диагонали равен 90°
⇒

Повторение
Если в параллелограмме диагональ делит углы пополам, то этот параллелограмм является ромбом
В ромбе диагонали пересекаются под прямым углом

Ответ: 30.
Модуль «ГЕОМЕТРИЯ» №9
Повторение (3)
∠А=∠ АDС=75°
∠ АDС=∠DСК=75°
∠DСК=∠ DКС=75°
75°
∠СDК=180°-2⋅75°=30°
АВСD параллелограмм.

Повторение
В равнобедренной трапеции углы при основании равны
При пересечении двух параллельных прямых третьей накрест лежащие углы равны
В равнобедренном треугольнике углы при основании равны

Ответ: 126.
Модуль «ГЕОМЕТРИЯ» №9
Повторение (2)
Углы ромба относятся как 3:7 .
Найти больший угол.
∠1+∠2=180°
Пусть х° - одна часть, тогда∠2=3х°, ∠1=7х°
3х+7х=180
10х=180
х=18
∠1=18°∙7=126°

Повторение
В ромбе противоположные стороны параллельны
Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°

Ответ: 130.
Модуль «ГЕОМЕТРИЯ» №9
Повторение (2)
Сумма двух углов параллелограмма равна 50°. Найти один из оставшихся углов.
∠А+∠С=50°
∠С+∠D=180°
∠D=180°-50°=130°

Повторение
В параллелограмме противоположные углы равны
Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°

Ответ: 80.
Модуль «ГЕОМЕТРИЯ» №9
Повторение (2)
Разность противолежащих углов трапеции равна 68°. Найти больший угол.
∠А+∠В=180°
Если ∠А=х°, то ∠В=х°+68°
х+х+68=180
2х=180-68
х=12
∠В=12°+68°=80°
∠В+∠С

Повторение
В равнобедренном треугольнике углы при основании равны.
Сумма углов, прилежащих боковой стороне трапеции равна 180°.

Модуль «ГЕОМЕТРИЯ» №9
Повторение (3)
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне.
D
В
С
А
О
1
4
3
2
∠DАВ+∠АВС=180°
Так как ∠1=∠2 и ∠3=∠4, то ∠3+∠2=90°
∠О=180°-(∠3+ ∠2)=90⁰
Ответ: 90.

Повторение
Сумма соседних углов параллелограмма равна 180⁰
Биссектриса – это луч, который делит угол пополам.
В треугольнике сумма углов равна 180°

Модуль «ГЕОМЕТРИЯ» №9
Повторение (3)
В
С
А
D
Найдите угол между гипотенузой и медианой, проведенной из прямого угла.
?
∠А+∠В=90°
Так как ∠С=∠А+∠В, то ∠В= ∠ВСD, ∠А= ∠АCD
47⁰
∠ВCD=47°
∠ВDC=180°-2∙47⁰=86⁰
Ответ: 86.

Повторение
В прямоугольном треугольнике сумма острых углов равна 90⁰
В равнобедренном треугольнике углы при основании равны
Сумма углов треугольника равна 180⁰

Модуль «ГЕОМЕТРИЯ» №9
В
1
4
3
2
О
С
А
100⁰
N
L
?
Найдите внешний угол при вершине С.
Повторение (3)
Так как ∠1=∠2, ∠3=∠4, то ∠2+∠3=1/2(∠А +∠В)
∠2+∠3=180°-100⁰=80⁰
⇒
∠А+∠В=80⁰∙2=160⁰
Внешний угол при вершине С равен 160⁰
Ответ: 160.

Повторение
Биссектриса – это луч, который делит угол пополам
В треугольнике сумма углов равна 180°
Внешний угол треугольника – это угол, смежный с углом треугольника и он равен сумме углов треугольника, не смежных с ним.

Модуль «ГЕОМЕТРИЯ» №9
Повторение (3)
В
С
А
26⁰
H
L
?
В ∆HLF ∠H=90⁰, ⇒ ∠HАL+∠HLA=90°
∠HLA внешний для ∆АLВ, ⇒ ∠HLA= ∠LАВ+∠В
⇒
∠HLA=90°-26⁰=64⁰
∆АLВ - равнобедренный, ⇒ ∠LАВ=∠В
∠В=½ ∠HLA= ½ ∙ 64⁰=32⁰
Ответ: 32.

Повторение
В прямоугольном треугольнике сумма острых углов равна 90°
Внешний угол треугольника равен сумме углов треугольника, не смежных с ним
В равнобедренном треугольнике углы при основании равны

Модуль «ГЕОМЕТРИЯ» №9
Повторение (2)
В
С
А
?
119⁰
O
Y
X
∠ВОС=∠XOY как вертикальные
⇒
∠XOY =119⁰
∠YOX+∠OYA+ ∠A+∠AXO =360°, где ∠OYA=∠AXO=90⁰
⇒
∠А=360⁰-2∙90⁰-⁰119⁰=61⁰
Ответ: 61.

Повторение
Вертикальными углами называются углы, стороны которых являются продолжением друг друга. Вертикальные углы равны.
Сумма углов четырехугольника равна 360°

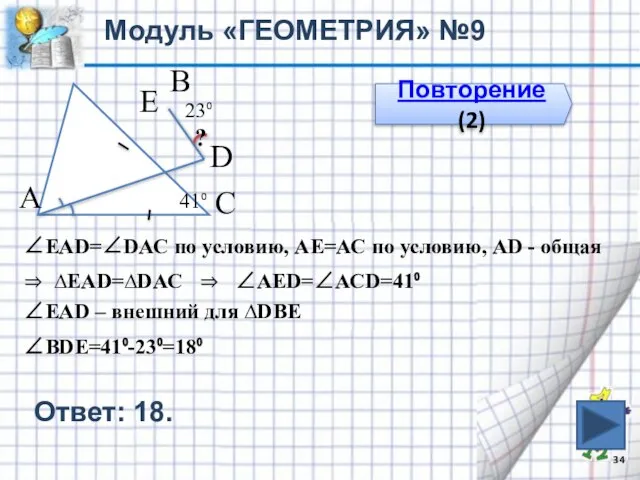
Модуль «ГЕОМЕТРИЯ» №9
Повторение (2)
41⁰
23⁰
В
С
А
?
Е
D
∠ЕАD=∠DАС по условию, АЕ=АС по условию, АD - общая
⇒
∆ЕАD=∆DАС
⇒
∠АЕD=∠АСD=41⁰
∠ЕАD – внешний для ∆DВЕ
∠ВDЕ=41⁰-23⁰=18⁰
Ответ: 18.

Повторение
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Модуль «ГЕОМЕТРИЯ» №9
В
С
А
10⁰
104⁰
Е
D
Найдите ∠ВDЕ.
?
Повторение (3)
∆СDЕ=∆СDВ
⇒
∠СВD и ∠АВС
⇒
∠СВD=180⁰-104⁰=76⁰
∠ЕСВ – внешний для ∆АВС
⇒
∠ЕСВ=104⁰+10⁰=114⁰
∠DСВ =½∠ЕСВ=57⁰
∠ЕDВ =2∠СDВ=2∙47⁰=94⁰
По сумме углов тр-ка ∠СDВ =180⁰-76⁰-57⁰=47⁰
Ответ: 94.

Повторение
Если в треугольниках две стороны и угол между ними равны, то треугольники равны
В равных треугольниках соответственные углы равны
Если угол разбит на части, то его градусная мера равна сумме градусных мер его частей

Модуль «ГЕОМЕТРИЯ» №9
В
С
А
Повторение (2)
sin A=0,8. Найдите sin B.
Ответ: 0,6.

Повторение
В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла
Основное тригонометрическое тождество:

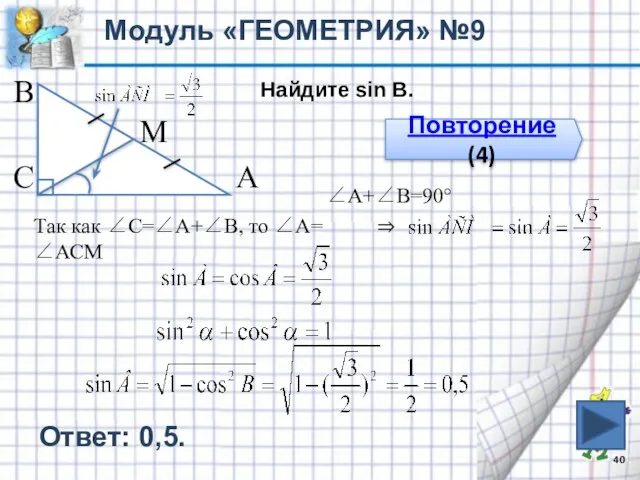
Модуль «ГЕОМЕТРИЯ» №9
В
С
А
М
Найдите sin B.
Повторение (4)
∠А+∠В=90°
Так как ∠С=∠А+∠В, то ∠А= ∠АСМ
⇒
Ответ: 0,5.

Повторение
В равнобедренном треугольнике углы при основании равны
В прямоугольном треугольнике сумма острых углов равна 90⁰
В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла
Основное тригонометрическое тождество: