Теорема о сумме углов треугольника

Цели урока:
Доказательство теоремы о сумме углов треугольника и следствия из нее;
Введение понятий остроугольного, тупоугольного и прямоугольного треугольников;
Применение полученных знаний при решении задач;
Развитие элементов геометрического мышления.

Ход урока.
I. Устная работа
А) Ответить на вопросы :
1) Какие прямые называются параллельными? Какие отрезки называются параллельными?
2) Сформулировать признаки параллельности прямых.
3) Сформулировать свойства параллельных прямых.
4) Сформулировать определение треугольника и назвать его элементы.

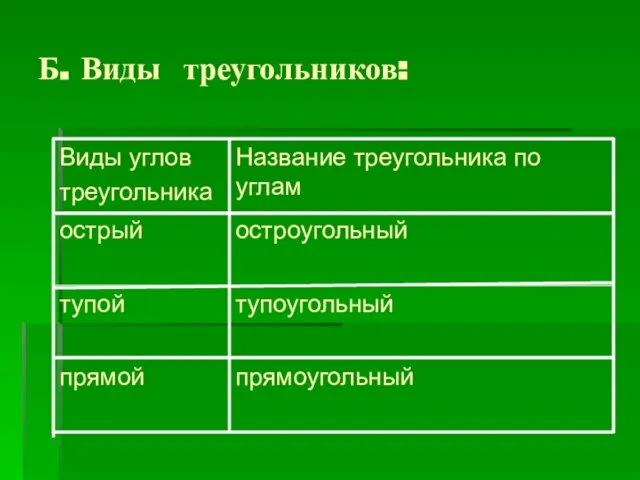
Б. Виды треугольников:

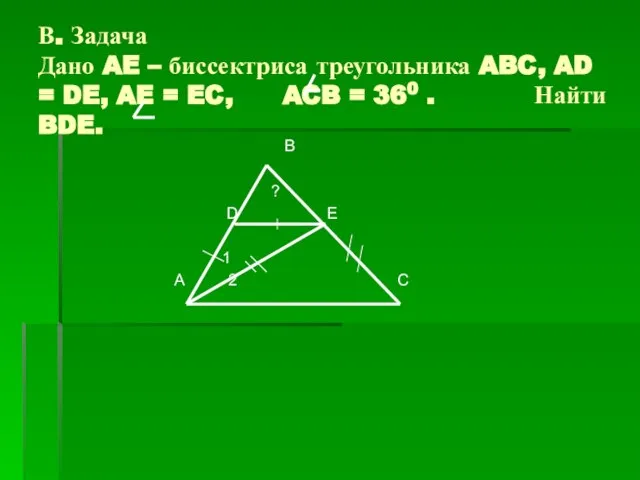
В. Задача
Дано AE – биссектриса треугольника ABC, AD = DE, AE = EC, ACB = 360 . Найти BDE.
B
?
D E
1
А 2 C

II. Изучение нового материала.
Практическая работа:
Начертить треугольник и найти сумму углов треугольника (с помощью транспортира); первый ряд – остроугольный, второй ряд – тупоугольный, третий ряд – прямоугольный.

2.Какие результаты получили, измеряя транспортиром углы треугольника?
Вывод: сумма углов треугольников близка к 1800 .

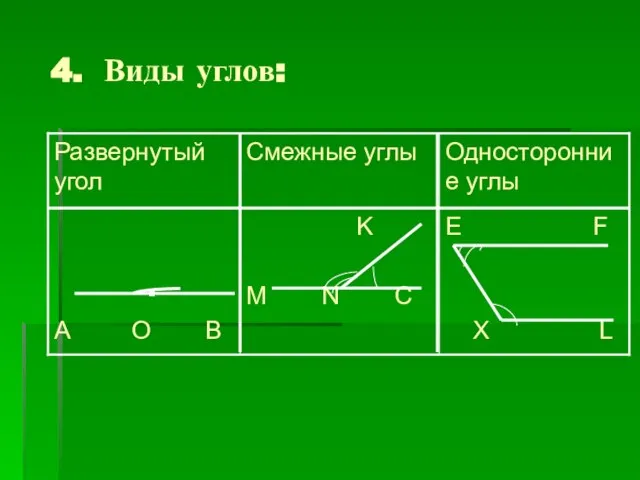
3.Где встречали это число?
1. Величина развернутого угла 1800
2. Сумма смежных углов равна 1800
3.Сумма односторонних углов равна 1800

4. Виды углов:

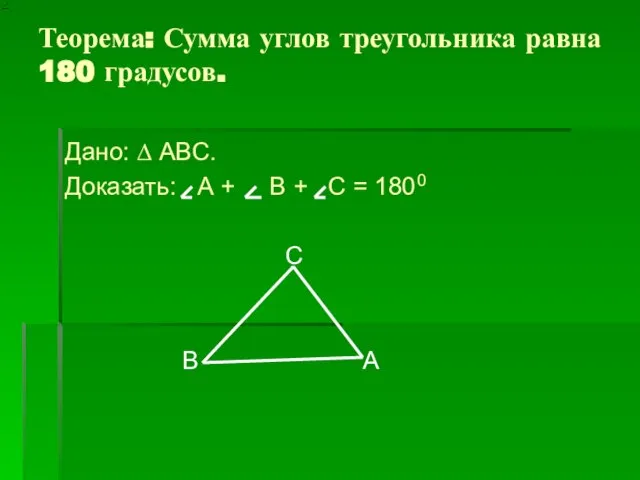
Теорема: Сумма углов треугольника равна 180 градусов.
Дано: ∆ ABC.
Доказать: А + B + C = 1800
C
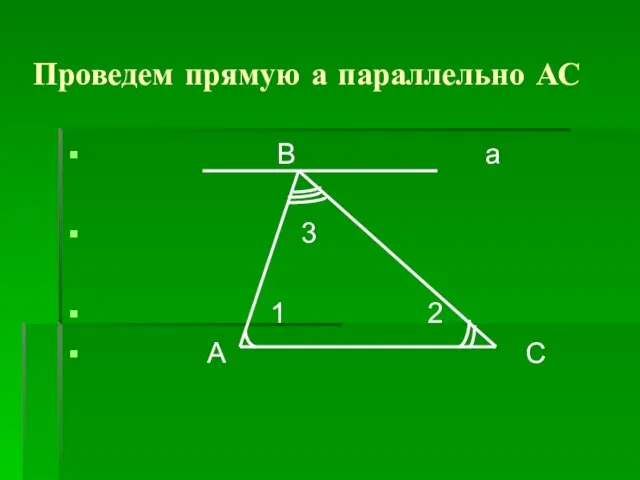
B A

Проведем прямую а параллельно АС
В а
3
1 2
А С

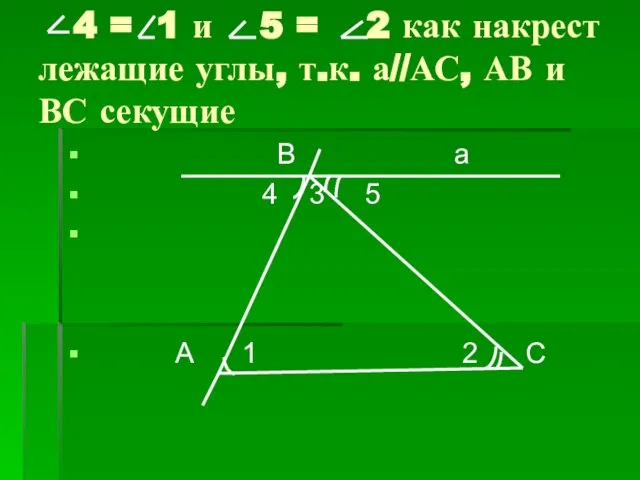
4 = 1 и 5 = 2 как накрест лежащие углы, т.к. а//АС, АВ и ВС секущие
В а
4 3 5
А 1 2 С

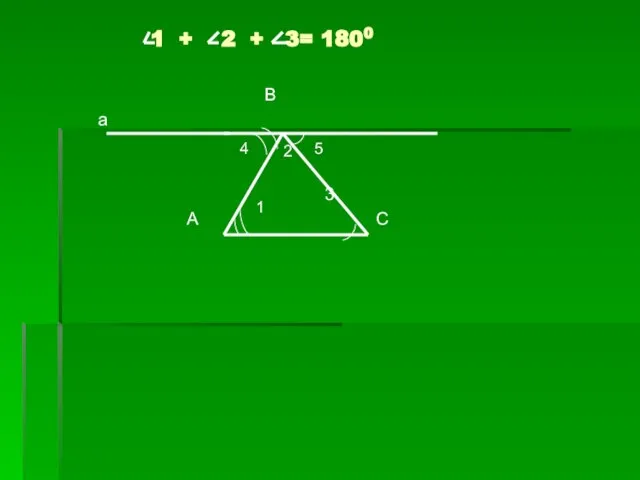
В
а
3
А С
1
2
5
4
1 + 2 + 3= 1800

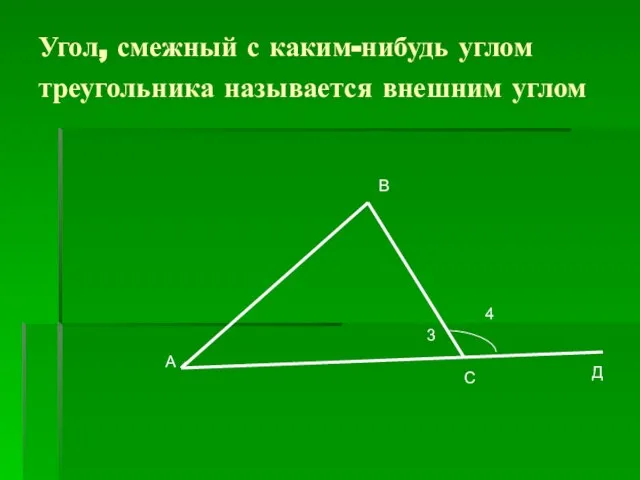
Угол, смежный с каким-нибудь углом треугольника называется внешним углом
А
В
С
Д
4
3

Практическая работа
1. Начертить треугольник и построить все внешние углы.
2. Сколько внешних углов можно построить у одного треугольника?
3. Какого вида могут быть внешние углы?
4. Всегда ли внешний угол тупой?
5.Могут ли все внешние углы быть тупыми? Острыми?
6 .Могут ли все внешние углы быть равными?

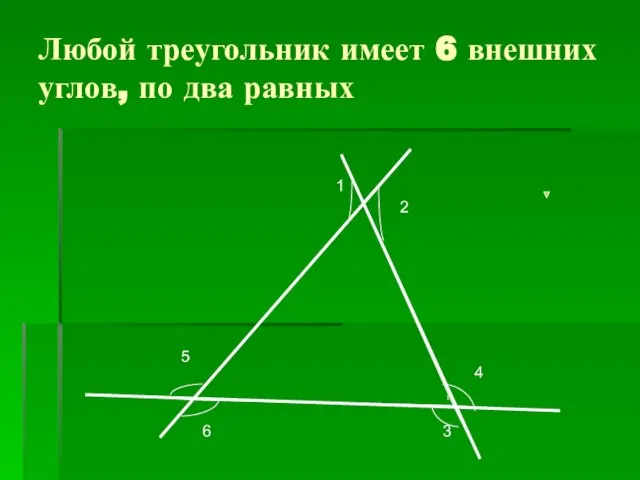
Любой треугольник имеет 6 внешних углов, по два равных
1
2
4
3
5
6

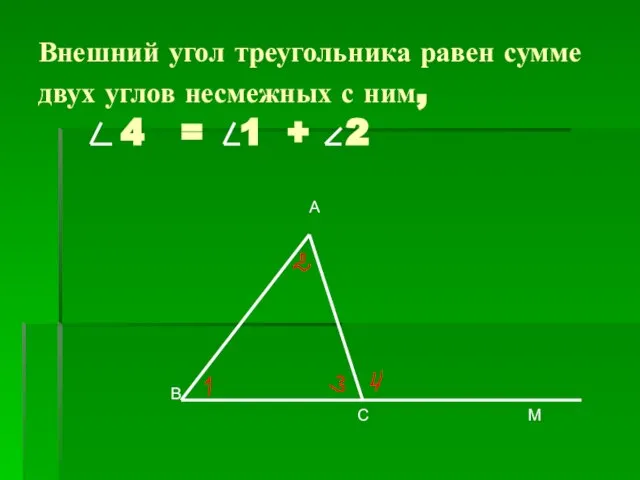
Внешний угол треугольника равен сумме двух углов несмежных с ним, 4 = 1 + 2
А
В
С
М

Остроугольные, тупоугольные, прямоугольные треугольники.
1. Остроугольный треугольник – имеет три острых угла.
2. Тупоугольный – один тупой угол.
3. Прямоугольный – один прямой угол.
В прямоугольном треугольнике – два катета и гипотенуза, гипотенуза лежит против прямого угла.

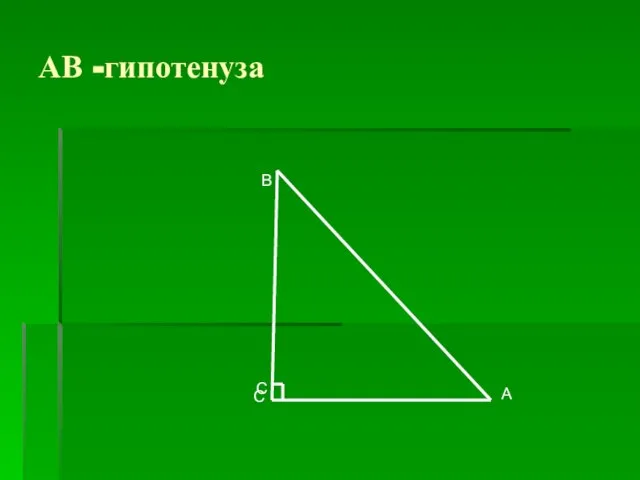
АВ -гипотенуза
С
А
С
В

Физкультминутка
Если устают глаза, снижается ваше внимание и активность, то
давайте дадим отдых глазам и себе.
1.Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза.
2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3-4 раза.
3.Медленно наклоняйте голову: вперед – влево – вправо - назад. Повторите 3-4 раза.
4.Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох.

Ответить на вопросы:
1. Если один из углов треугольника прямой, то какими будут два других угла?
2. Если треугольник прямоугольный, то чему равна сумма острых углов треугольника?
3. Если один из углов треугольника тупой, то чему равна сумма двух других углов?
4.Могут ли все три угла треугольника быть равными?
5. Чему равна градусная мера каждого из них?
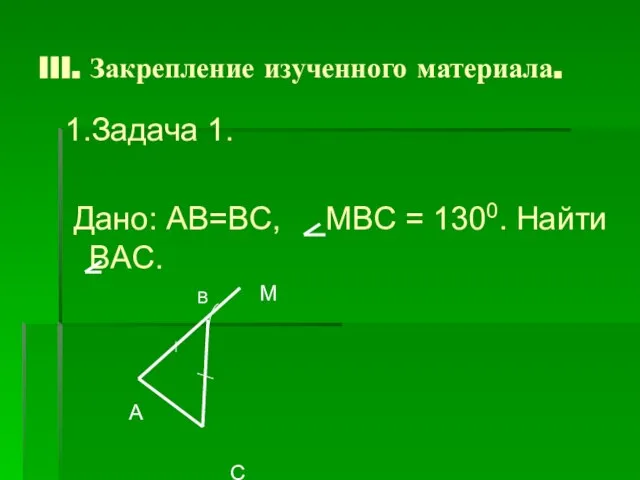
6. Могут ли все углы треугольника быть острыми?

III. Закрепление изученного материала.
1.Задача 1.
Дано: AB=BC, MBC = 1300. Найти BAC.
M
A C
В

Решение задачи 1.
Так как АВ=ВС, то АВС – равнобедренный, значит, А = С.
МВС внешний угол АВС,
МВС = А + С = 130 º.
А + С= 130 º. А = С =130 º : 2 = 65 º
ВАС = 65 º .

2. Задача №2
Найти углы треугольника АВС, если углы треугольника относятся как
3:5:10.

Решение задачи №2
1). 3+5+10=18
2).180º :18=10º
3).10º *3=30º
4).10º *5=50º
5).10º *10=100º

3. № 225
Доказать, что каждый угол равностороннего треугольника равен 60 º

4. Самостоятельная работа
Найти углы треугольника, если углы относятся, как:
Вариант 1 - 5:6:7;
Вариант 2 – 3:4:2
Вариант 3 - 5:2:2 ;

Проверка самостоятельной работы:
Вариант 1
50º ; 60º ; 70º :
Вариант 2
60º ; 80º ; 40º ;
Вариант 3
100º ; 40º ; 40º ;