Слайд 2Параллелепипед
Параллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Параллелепипед имеет 8

вершин и 12 рёбер. Грани параллелепипеда, не имеющие общих вершин, называются противоположными.
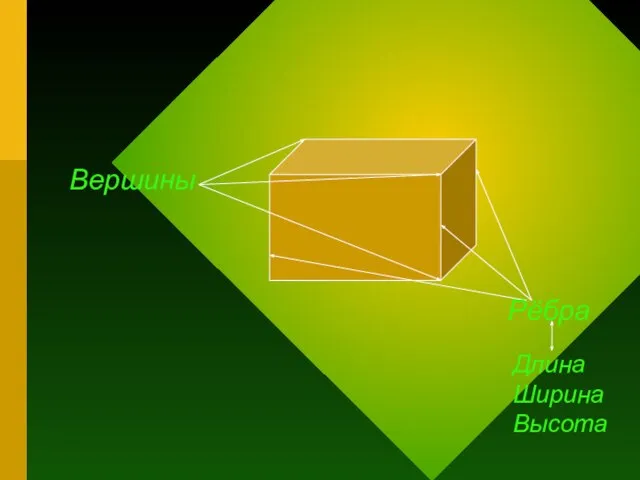
Слайд 3Вершины
Рёбра
Длина
Ширина
Высота
Слайд 4Параллелепипед
Они равны и лежат в параллельных плоскостях. Диагонали параллелепипеда, то есть отрезки,

соединяющие вершины параллелепипеда, не принадлежащие какой – либо одной грани, пересекаются в одной точке и делятся ею по полам.
Слайд 5Параллелепипед
Параллелепипед называется прямым или прямоугольным, если все его грани – прямоугольники; это

- прямая четырёхугольная призма. Параллелепипед, все грани которого квадраты, называется кубом.
Слайд 6Параллелепипед
Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называются его измерениями. Квадрат

длинны диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Слайд 7Параллелепипед
Объём параллелепипеда равен произведению площади основания (какой – либо его грани) на

высоту (расстояние между основанием и противоположной гранью). Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Слайд 8Параллелепипед
Название «параллелепипед» происходит от греческого слова «параллелос», означающего «параллельный», и греческого слова

«эпипедос», означающего «плоскость», «поверхность». Слово встречалось у древнегреческих ученых Евклида и Герона.
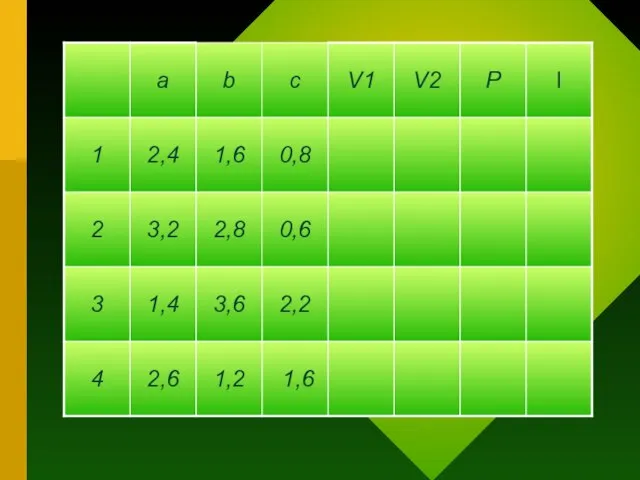
Слайд 9Объём прямоугольного параллелепипеда.
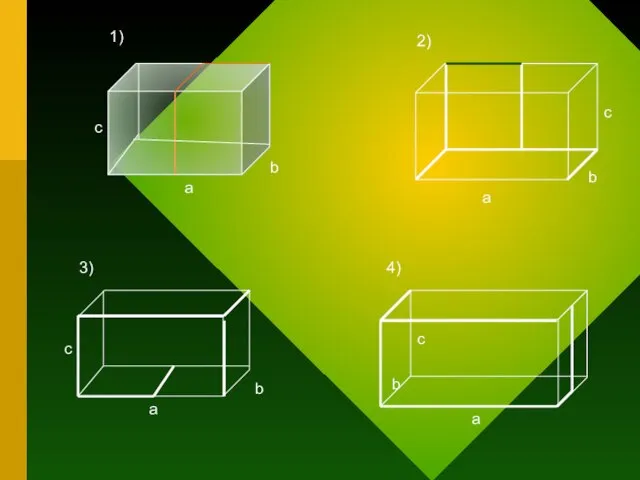
Найди объём V1 прямоугольного параллелепипеда с размерами a, b и

c, сумму Р длин всех его рёбер и длину l жирной линии, у которой концы и точки перегиба – вершины параллелепипеда или середины его рёбер. Найди объём V2 параллелепипеда с размерами в два раза меньше.
Слайд 10
Представь положение жирной линии в пространстве и согни её из проволоки.










 Сферическая поверхность. Шар Геометрия 11 класс
Сферическая поверхность. Шар Геометрия 11 класс Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости Введение в стереометрию
Введение в стереометрию Средняя линия треугольника 8 класс
Средняя линия треугольника 8 класс Круги Эйлера и их практическое применение
Круги Эйлера и их практическое применение Приготовьтесь к построению
Приготовьтесь к построению Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области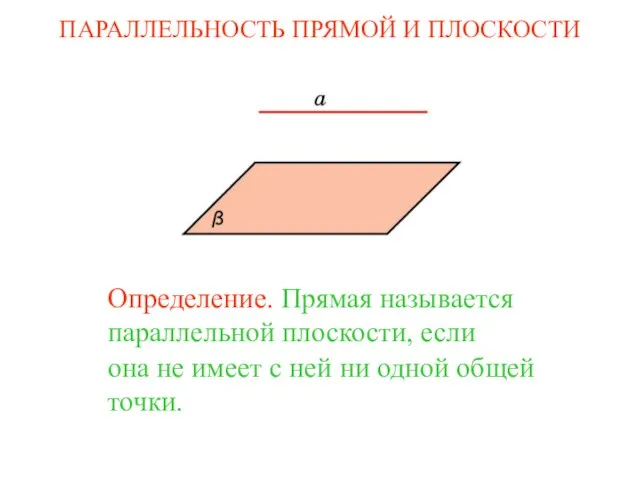 Параллельность прямой и плоскости
Параллельность прямой и плоскости Свойство точек биссектрисы угла.
Свойство точек биссектрисы угла. Вокруг храма с линейкой и циркулем
Вокруг храма с линейкой и циркулем Теорема о трех перпендикулярах в задачах 10 заочное обучение
Теорема о трех перпендикулярах в задачах 10 заочное обучение Виды углов. Измерение углов
Виды углов. Измерение углов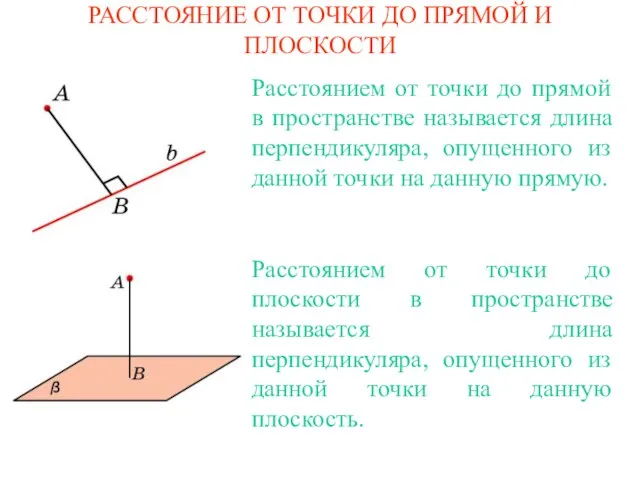 Расстояние от точки до прямой и плоскости
Расстояние от точки до прямой и плоскости Прямоугольник и его свойства
Прямоугольник и его свойства Пирамиды
Пирамиды Пифагоровы штаны во все стороны равны
Пифагоровы штаны во все стороны равны Координатный метод
Координатный метод Приращение функции и приращение аргумента
Приращение функции и приращение аргумента Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Решение прямоугольных треугольников
Решение прямоугольных треугольников Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников Первый признак равенства треугольников
Первый признак равенства треугольников Первый урок геометрии в 7 классе
Первый урок геометрии в 7 классе Смежные и вертикальные углы
Смежные и вертикальные углы вид разреза сечения
вид разреза сечения Секреты квадрата и кубика
Секреты квадрата и кубика