Содержание
- 2. На уроках геометрии в 7 классе мы изучали треугольник и его свойства. Небольшие исторические справки к
- 3. ЦЕЛЬ МОЕГО ПРОЕКТА Изучить материалы и существующую литературу по данному вопросу. Понять роль этой геометрической фигуры
- 4. Работая над проектом, я искала информацию в справочниках, энциклопедиях и в Интернете. Некоторые факты показавшиеся мне
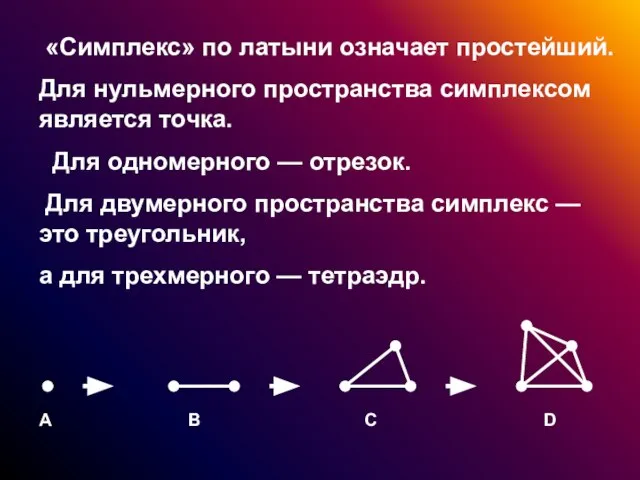
- 5. «Симплекс» по латыни означает простейший. Для нульмерного пространства симплексом является точка. Для одномерного — отрезок. Для
- 6. Треугольник – это простейшая фигура: три стороны и три вершины
- 7. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных
- 8. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади
- 9. Через 2000 лет в Древней Греции изучение свойств треугольника ведется очень активно. Пифагор открывает свою теорему.
- 10. Особенно активно свойства треугольника исследовались в XV – XVI веках. Одна из красивейших теорем того времени
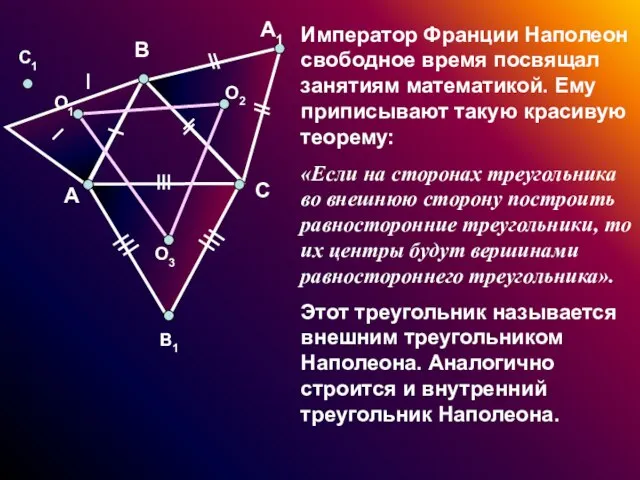
- 11. Император Франции Наполеон свободное время посвящал занятиям математикой. Ему приписывают такую красивую теорему: «Если на сторонах
- 12. Огромное количество работ по геометрии треугольника, проведенное в XV – XIX веках, создало впечатление, что о
- 13. ЭТАПЫ РАЗВИТИЯ МАТЕМАТИКИ I. ЗАРОЖДЕНИЕ МАТЕМАТИКИ (Первобытнообщинный строй, каменный век, рабовладельческий строй): Оформление чувства геометрическ- ой
- 14. ВЫВОДЫ: В результате проведенных исследований материалов по рассматриваемому вопросу я узнала, что Треугольник изучался на протяжении
- 16. Скачать презентацию











 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием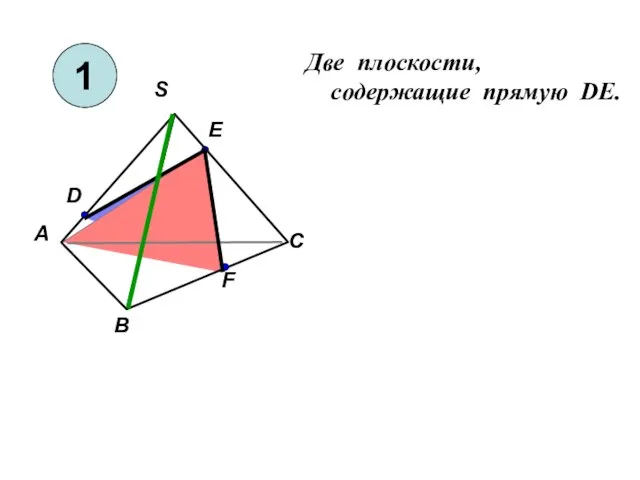 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия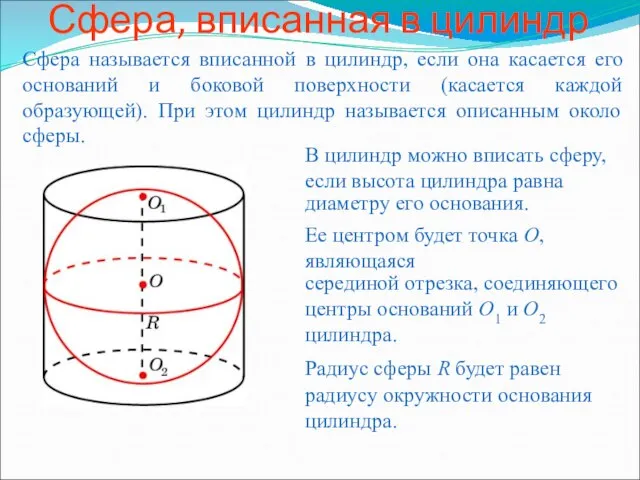 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика