Положение плоскости относительно плоскостей проекций

Плоскости частного положения

Плоскость, перпендикулярная к плоскости проекций, называется проецирующей
Особенности
проецирующих плоскостей:
– одна проекция любого элемента, расположенного
– в проецирующей плоскости, совпадает
с соответствующим следом этой плоскости
– угол наклона заданной плоскости к плоскости проекций на эпюре проецируется в натуральную величину
Проецирующие плоскости

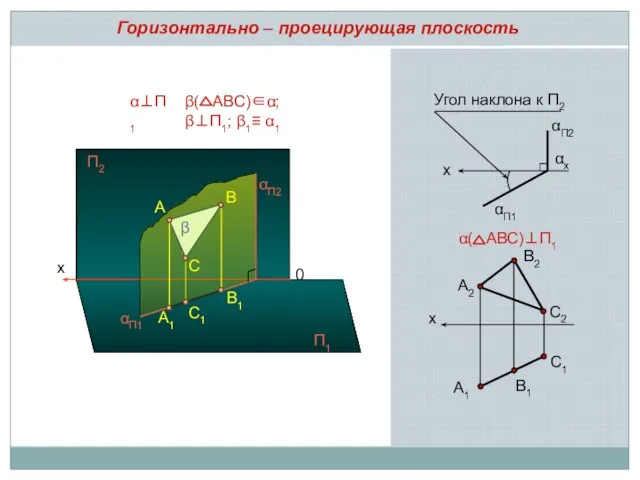
х
А2
В2
С2
С1
А1
В1
α( АВС)⊥П1
Горизонтально – проецирующая плоскость
x
αП1
αx
Угол наклона к П2
x
A1
B1
A
0
B
C
αП2
С1
П2
П1
α⊥П1
β
β( АВС)∈α; β⊥П1; β1≡ α1
αП1
αП2

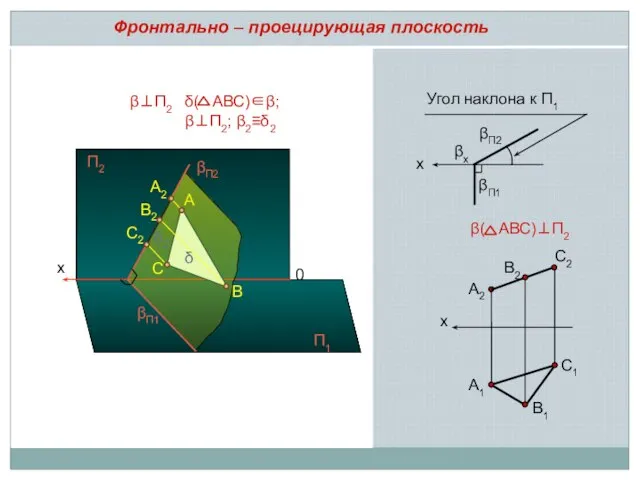
x
A2
B2
A
0
B
C
βП2
βП1
С2
П2
П1
β⊥П2
δ
δ( АВС)∈β; β⊥П2; β2≡δ2
х
А2
В2
С2
С1
А1
В1
β( АВС)⊥П2
x
βП1
βП2
βx
Угол наклона к П1
Фронтально – проецирующая плоскость
δ2

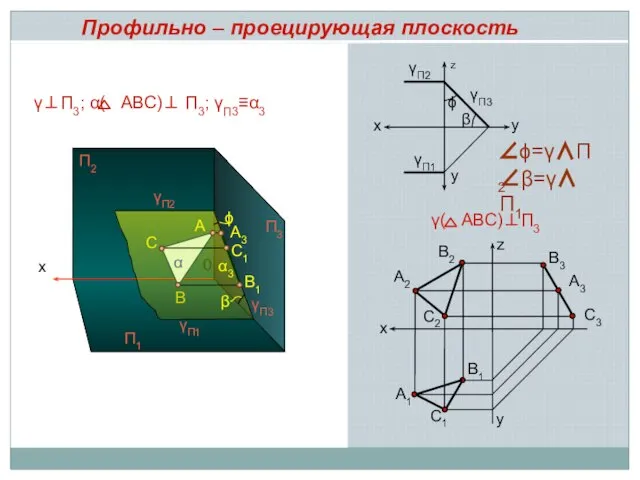
x
A
0
B
C
γП2
γП1
П2
П1
A3
С1
B1
П3
α
х
А3
В3
С3
С1
А1
В1
В2
А2
С2
γ( АВС)⊥П3
Профильно – проецирующая плоскость
z
y
x
γП1
γП2
γП3
z
у
у
ϕ
β
∠ϕ=γ∧П2
∠β=γ∧П1
γП3
α3
γ⊥П3; α( АВС)⊥ П3; γП3≡α3
ϕ
β

Плоскость,
параллельная к плоскости проекций, называется плоскостью уровня
Особенности
плоскостей уровня:
Плоскости уровня
– любая плоская фигура,
расположенная в плоскости уровня,
проецируется на параллельную ей плоскость проекций без искажения, – т.е. в натуральную величину

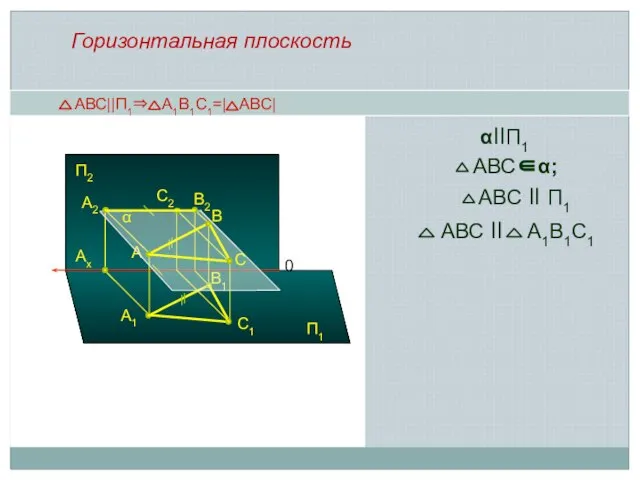
АВС||П1⇒ А1В1С1=| АВС|
A1
B1
A
A2
Ax
0
B
B2
αllП1
С1
С2
α
Горизонтальная плоскость
П2
П1
АВС∈α;
АВС ll П1
АВС ll А1В1С1
С