Содержание
- 2. Определения Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято
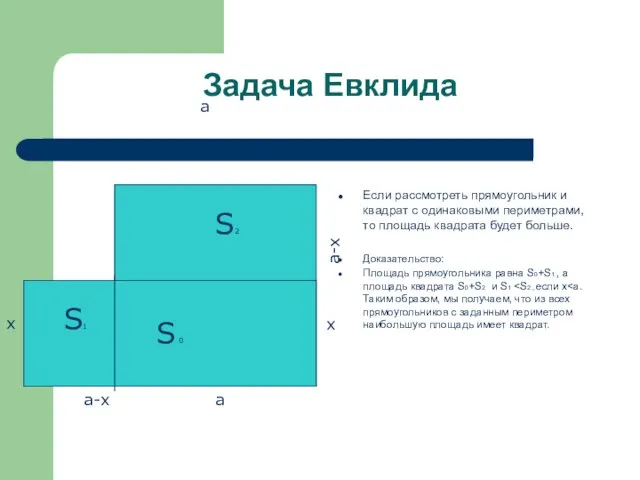
- 3. Задача Евклида Если рассмотреть прямоугольник и квадрат с одинаковыми периметрами, то площадь квадрата будет больше. Доказательство:
- 4. Легенда о Дионе Диона- основательница города Карфагена и его первая царица. Вынужденная бежать из своего города,
- 5. Задачи Зенодора (2-1 в. до н.э.) Из всех многоугольников с равным периметром и равным числом сторон
- 6. Задача Дионы (частный случай) Если принять, что береговая линия есть прямая и ограничиваемый участок прямоугольной формы,
- 8. Скачать презентацию




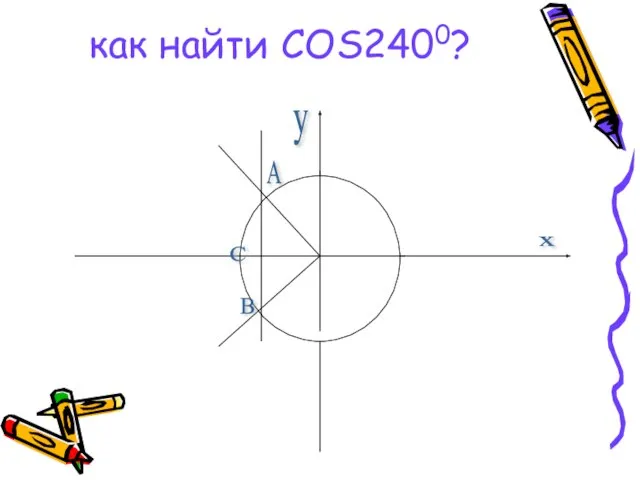 Косинус
Косинус Итоговое повторение курса геометрии
Итоговое повторение курса геометрии Цилиндр и конус
Цилиндр и конус Преобразования на плоскости
Преобразования на плоскости ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга
ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга Правильный додекаэдр
Правильный додекаэдр Основные формулы тригонометрии
Основные формулы тригонометрии Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Векторы 9 класс
Векторы 9 класс В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ вид разреза сечения
вид разреза сечения Окружность в аксонометрии
Окружность в аксонометрии Параллельность в пространстве
Параллельность в пространстве Биссектриса угла
Биссектриса угла Правильные многогранники
Правильные многогранники Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Площади и объемы - презентация по Геометрии_
Площади и объемы - презентация по Геометрии_ Геометрические фигуры (Взаимное расположение на плоскости)
Геометрические фигуры (Взаимное расположение на плоскости) Приготовьтесь к построению
Приготовьтесь к построению План –конспект урока. Тема: «Треугольник» 5 класс.
План –конспект урока. Тема: «Треугольник» 5 класс. ЭЛЛИПС
ЭЛЛИПС Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Сумма двух векторов Геометрия -9 Урок 4
Сумма двух векторов Геометрия -9 Урок 4 Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны
Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны Почему квадрат?
Почему квадрат? Теорема синусов 9 класс
Теорема синусов 9 класс Свойство и признак описанного четырёхугольника
Свойство и признак описанного четырёхугольника Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_