Содержание
- 2. Содержание История появления Определение пирамиды Виды пирамид Площадь пирамиды Правильная пирамида Свойство пирамиды Апофема Теорема о
- 3. История появления Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило
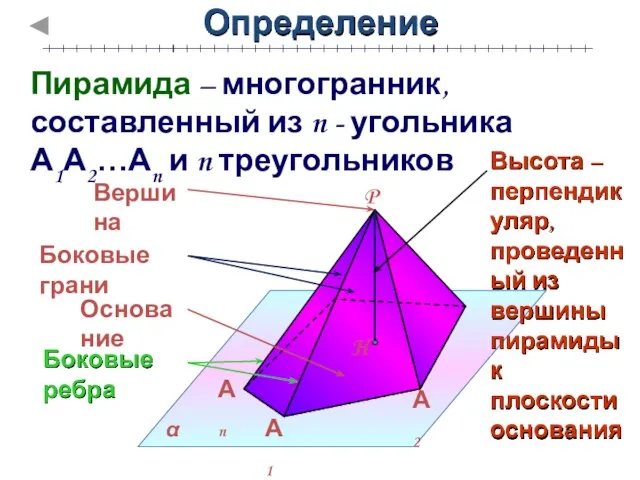
- 4. Определение Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольников Высота – перпендикуляр,
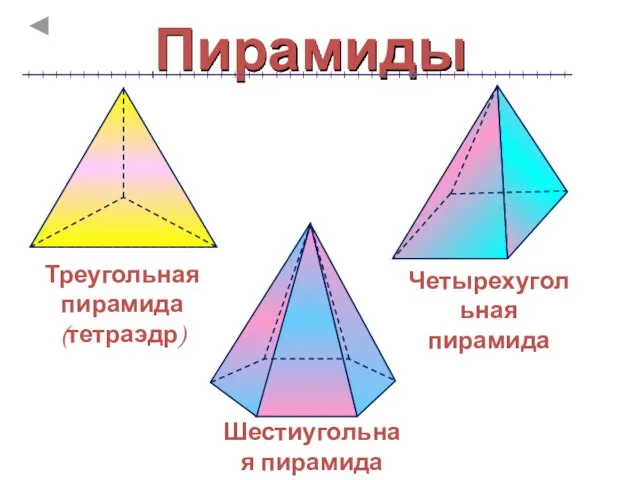
- 5. Пирамиды Треугольная пирамида (тетраэдр) Шестиугольная пирамида Четырехугольная пирамида
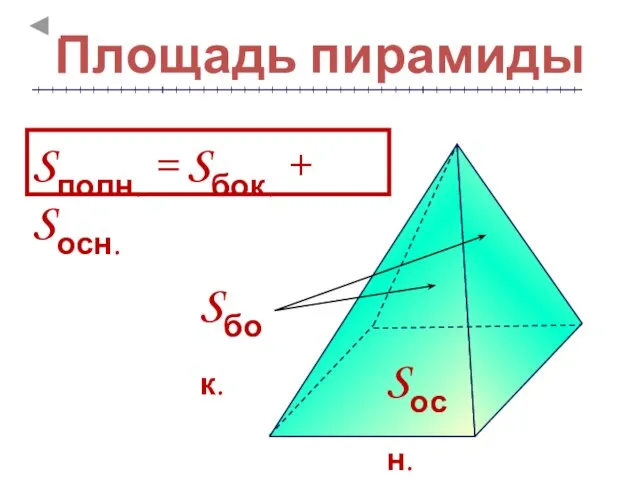
- 6. Площадь пирамиды Sполн. = Sбок. + Sосн. Sбок. Sосн.
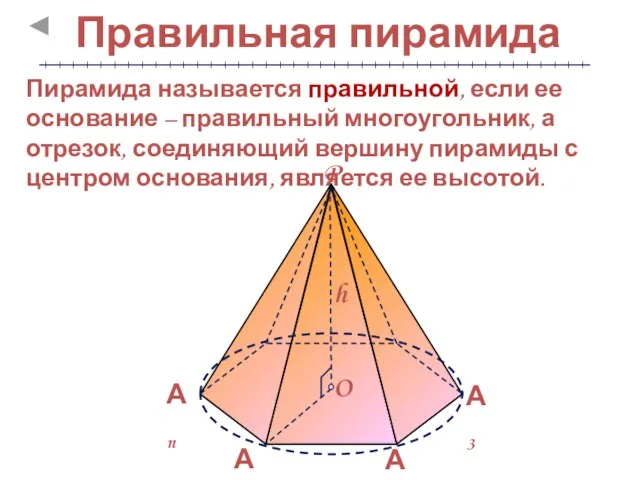
- 7. Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды
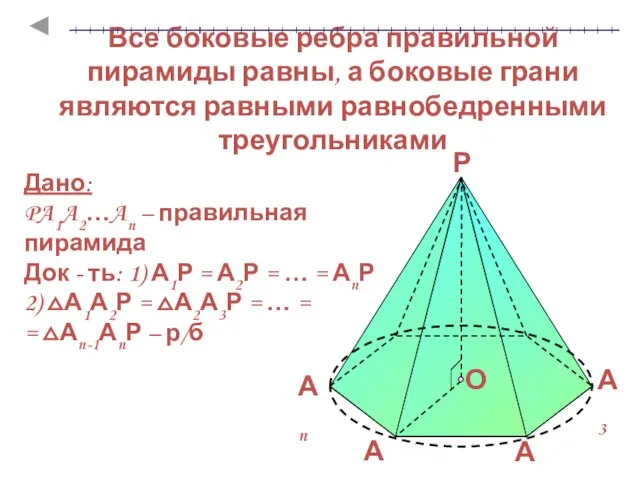
- 8. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками Дано: PA1A2…An –
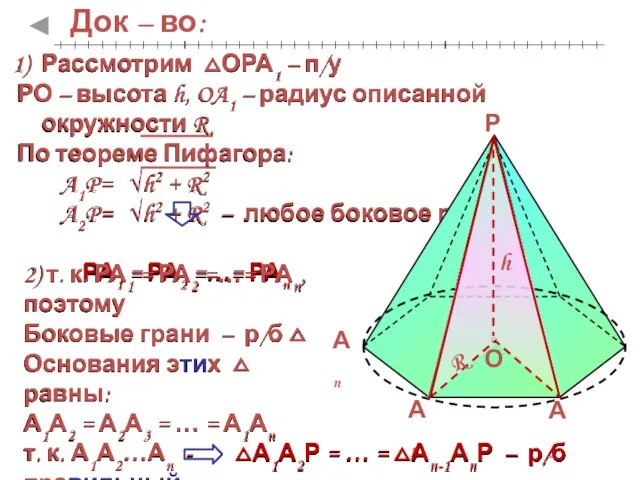
- 9. Док – во: 2) т. к. РА1 = РА2 =…= РАn, поэтому Боковые грани – р/б
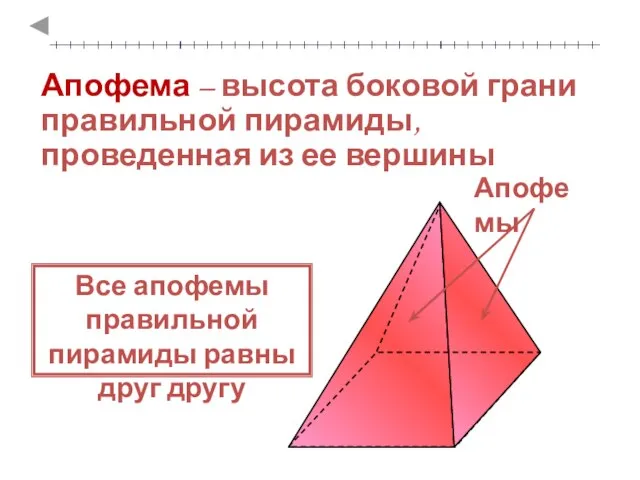
- 10. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины Все апофемы правильной пирамиды равны
- 11. Теорема о площади боковой поверхности правильной пирамиды Площадь боковой поверхности правильной пирамиды равна половине произведения периметра
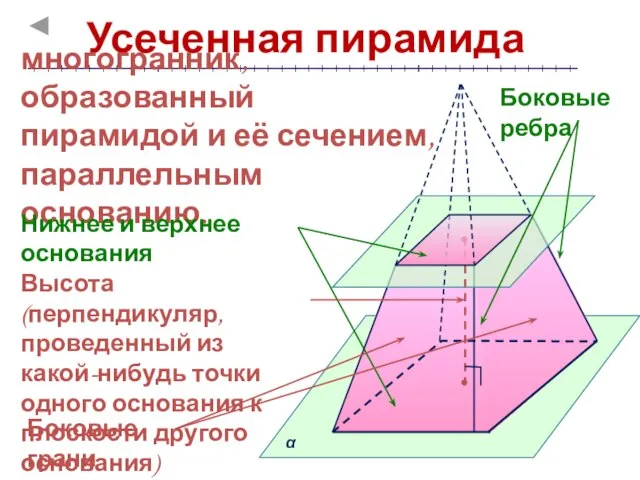
- 12. Усеченная пирамида многогранник, образованный пирамидой и её сечением, параллельным основанию. Нижнее и верхнее основания Боковые грани
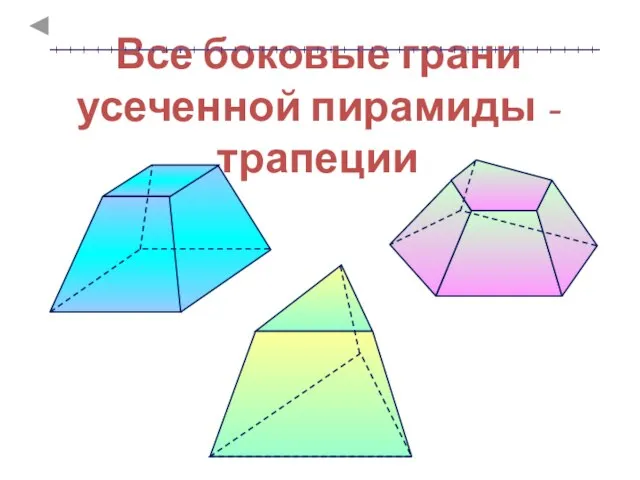
- 13. Все боковые грани усеченной пирамиды - трапеции
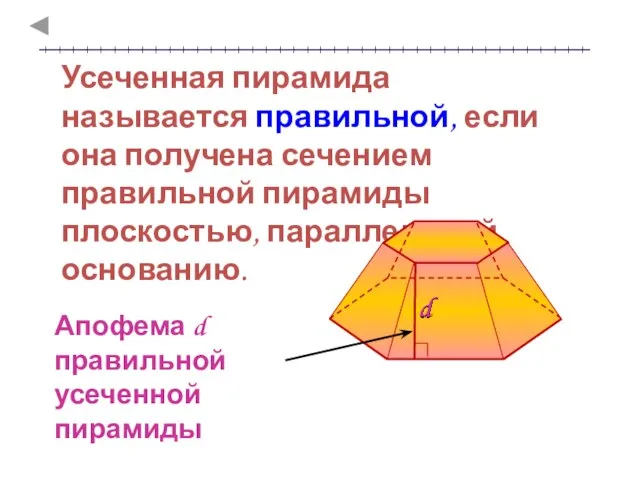
- 14. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Апофема d правильной
- 16. Скачать презентацию



 ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Путешествие в страну Геометрия
Путешествие в страну Геометрия Сфера. Шар
Сфера. Шар Начертательная геометрия
Начертательная геометрия Решение задач по курсу геометрии
Решение задач по курсу геометрии Проецирование точки на три плоскости
Проецирование точки на три плоскости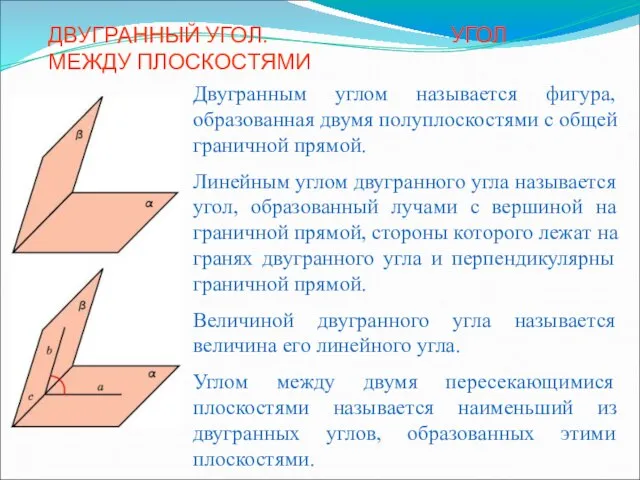 Двугранный угол. Угол между плоскостями
Двугранный угол. Угол между плоскостями Геометрические задачи «С2» - презентация по Геометрии_
Геометрические задачи «С2» - презентация по Геометрии_ Основные свойства простейших геометрических фигур
Основные свойства простейших геометрических фигур Карточки - задания по теме "Конус"
Карточки - задания по теме "Конус" Площадь 8 КЛАСС
Площадь 8 КЛАСС Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости Геометрия. Как она возникла?
Геометрия. Как она возникла? Учитель Лемешкина А.М.
Учитель Лемешкина А.М. Периметр. Площа - презентация по Геометрии_
Периметр. Площа - презентация по Геометрии_ Классификация геометрических объектов
Классификация геометрических объектов Треугольники 3 класс
Треугольники 3 класс Флексагоны флексоры
Флексагоны флексоры Параллелепипед
Параллелепипед Цилиндр и конус - презентация по Геометрии
Цилиндр и конус - презентация по Геометрии Логарифм. Основные понятия
Логарифм. Основные понятия Правильные выпуклые многогранники
Правильные выпуклые многогранники Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А.
Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А. Развитие пространственного мышления
Развитие пространственного мышления Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Фракталы и их применение в наши дни
Фракталы и их применение в наши дни Геометрические задачи на экстремум
Геометрические задачи на экстремум Показательная функция и её применение
Показательная функция и её применение