Правильная пирамида

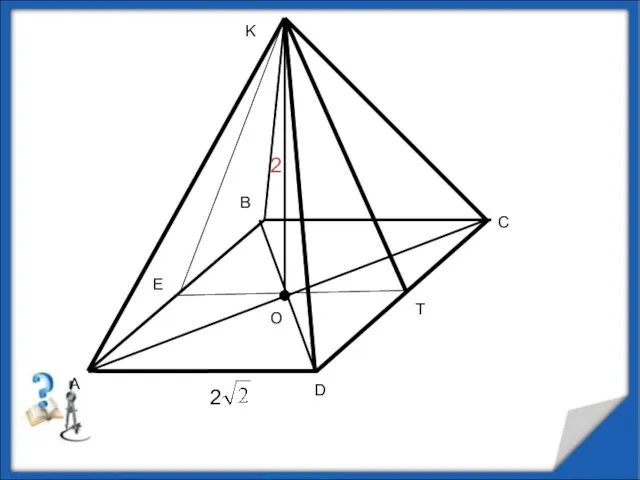
A
D
C
B
O
K
T
E
2

В правильной четырехугольной пирамиде известны длина стороны основания 2 и длина высоты 2. Найдите:
а) объем пирамиды;
б) площадь боковой по­верхности;
в) угол наклона бокового ребра к плоскости основания;
г) угол наклона боковой грани к плоскости основания;
д) радиус вписанного шара;
е) радиус описанного шара;
ж) расстояние от вершины пирамиды до плоскости основания;

Выход
з) расстояние от вершины пирамиды до ребра основания;
и) расстояние от ребра основания до противоположной грани;
к) расстояние между боковым ребром и скрещивающейся с ним диагональю ос­нования;
л) объем вписанного конуса;
м) площадь боковой поверхности описанного конуса.
Выход

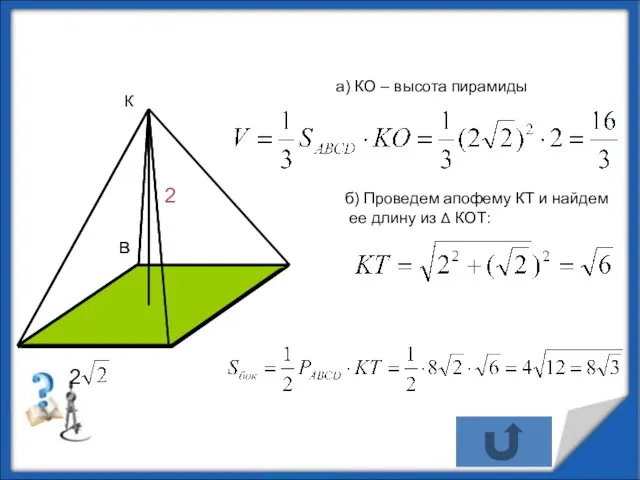
а) КО – высота пирамиды
В
О
К
2
б) Проведем апофему КТ и найдем
ее длину из Δ КОТ:
В

В) Так как в правильной пирамиде все
углы наклона всех боковых ребер к
плоскости основания равны, то найдем
например, <КСО. Рассмотрим ΔКСО
КО=2, ОС=0,5 АС, где АС – диагональ
квадрата АВСD, значит
К
О
?

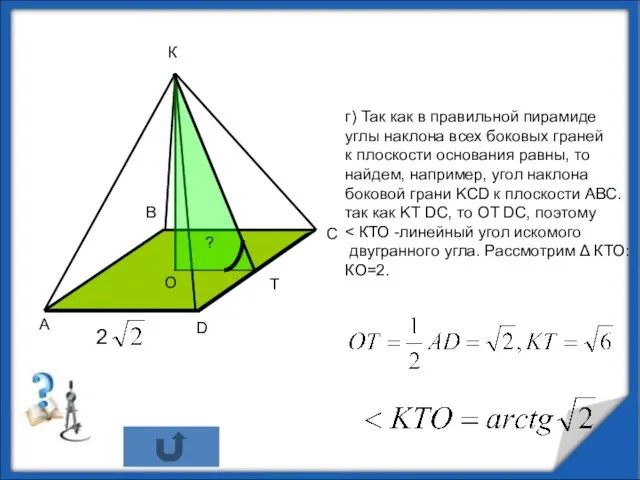
г) Так как в правильной пирамиде
углы наклона всех боковых граней
к плоскости основания равны, то
найдем, например, угол наклона
боковой грани KCD к плоскости АВС.
так как KT DC, то OT DC, поэтому
< КТО -линейный угол искомого
двугранного угла. Рассмотрим Δ КТО:
КО=2.
Т
К
О
?

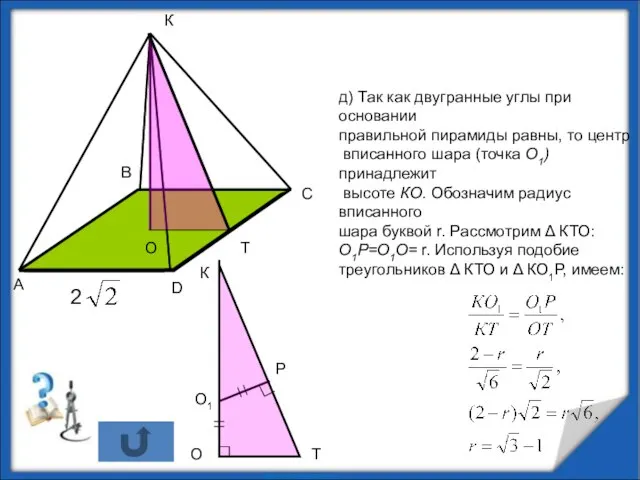
д) Так как двугранные углы при основании
правильной пирамиды равны, то центр вписанного шара (точка О1) принадлежит
высоте КО. Обозначим радиус вписанного
шара буквой r. Рассмотрим Δ КТО:
О1Р=О1О= r. Используя подобие треугольников Δ КТО и Δ КО1Р, имеем:
К
Т
О

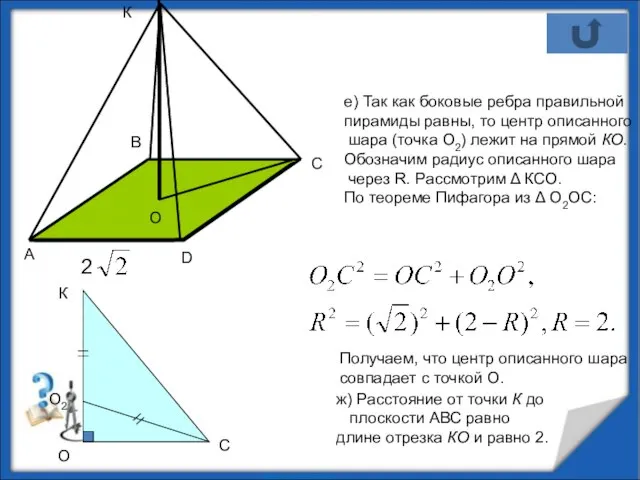
е) Так как боковые ребра правильной
пирамиды равны, то центр описанного
шара (точка О2) лежит на прямой КО.
Обозначим радиус описанного шара
через R. Рассмотрим Δ КСО.
По теореме Пифагора из Δ О2ОС:
Получаем, что центр описанного шара
совпадает с точкой О.
К
О
О2
О
К
С
ж) Расстояние от точки К до
плоскости АВС равно
длине отрезка КО и равно 2.

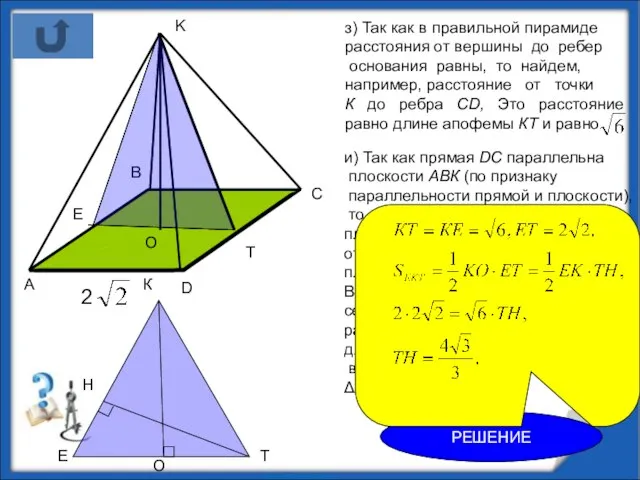
з) Так как в правильной пирамиде
расстояния от вершины до ребер основания равны, то найдем,
например, расстояние от точки
К до ребра СD, Это расстояние
равно длине апофемы КТ и равно
K
O
T
и) Так как прямая DС параллельна
плоскости АВК (по признаку
параллельности прямой и плоскости),
то расстояние от прямой DС до
плоскости АВК равно расстоянию
от любой точки прямой DС до этой
плоскости. Рассмотрим на прямой
ВС точку Т. И из Δ ЕКТ (точка Е —
середина АВ) найдем искомое
расстояние. Это расстояние равно
длине высоты ТН. Найдем длину ТН,
выразив двумя способами площадь
Δ ЕКТ.
Е
РЕШЕНИЕ

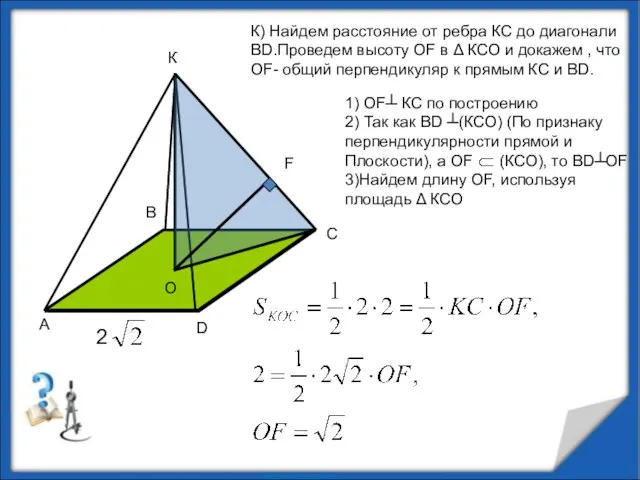
К
К) Найдем расстояние от ребра КС до диагонали
ВD.Проведем высоту OF в Δ КСО и докажем , что
OF- общий перпендикуляр к прямым КС и ВD.
1) OF┴ КС по построению
2) Так как ВD ┴(КСО) (По признаку
перпендикулярности прямой и
Плоскости), а OF (КСО), то ВD┴OF
3)Найдем длину OF, используя
площадь Δ КСО
О
F

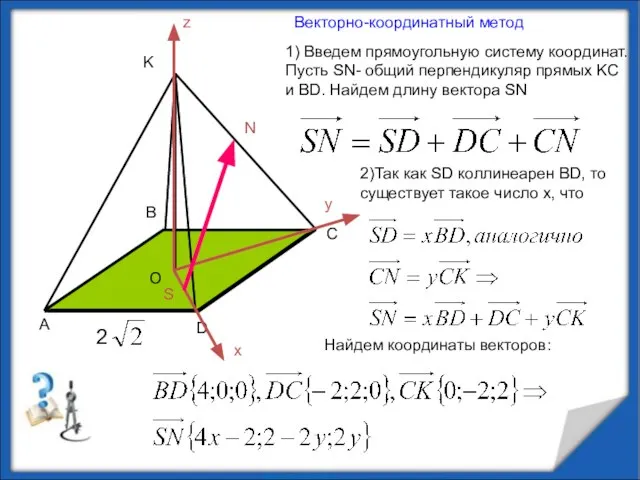
1) Введем прямоугольную систему координат.
Пусть SN- общий перпендикуляр прямых KC
и BD. Найдем длину вектора SN
2)Так как SD коллинеарен BD, то
существует такое число х, что
Найдем координаты векторов:
Векторно-координатный метод
z
x
y
K
O
S
N

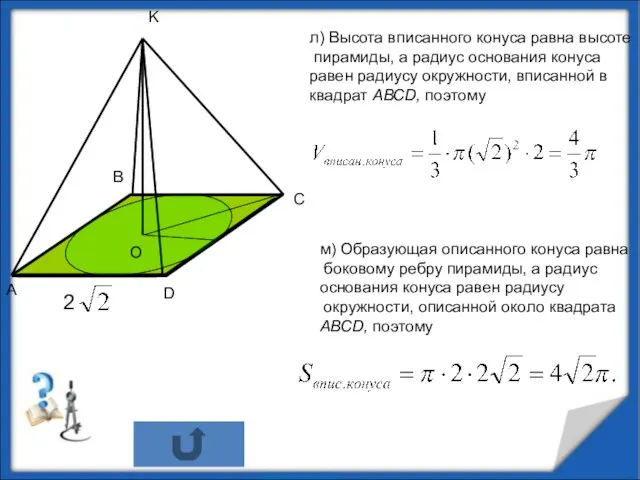
л) Высота вписанного конуса равна высоте
пирамиды, а радиус основания конуса
равен радиусу окружности, вписанной в
квадрат АВСD, поэтому
м) Образующая описанного конуса равна
боковому ребру пирамиды, а радиус
основания конуса равен радиусу
окружности, описанной около квадрата
АВСD, поэтому
K
O