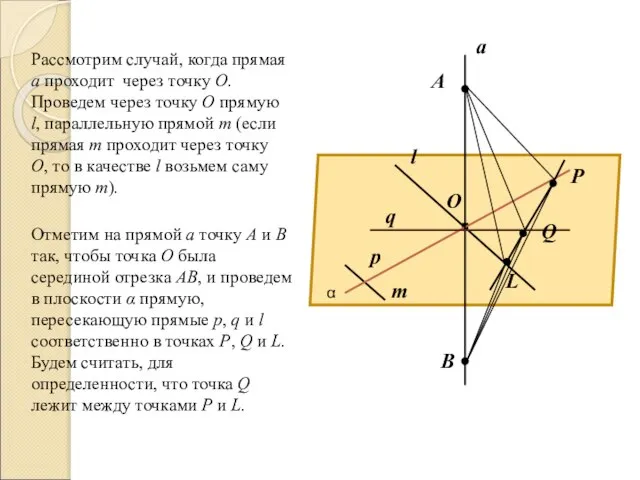
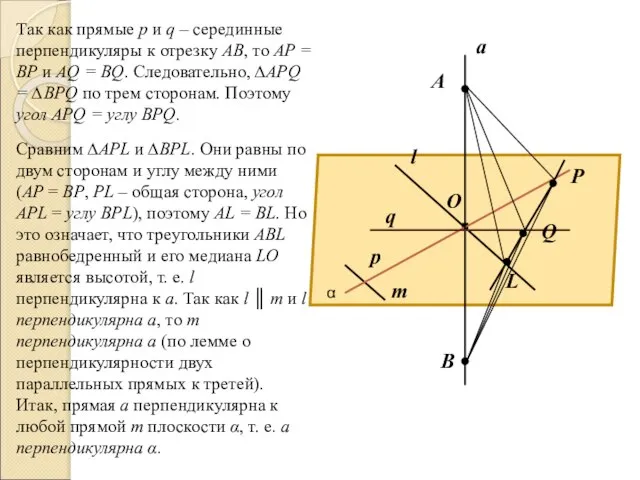
то АР = ВР и AQ = BQ. Следовательно, ∆APQ = ∆BPQ по трем сторонам. Поэтому угол APQ = углу BPQ.
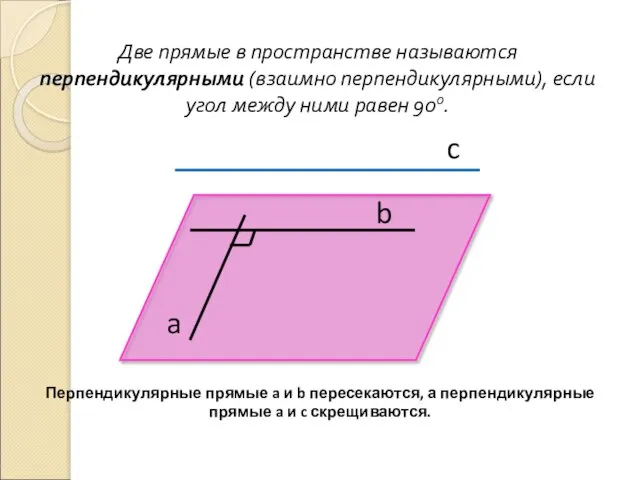
Сравним ∆APL и ∆BPL. Они равны по двум сторонам и углу между ними (AP = BP, PL – общая сторона, угол APL = углу BPL), поэтому AL = BL. Но это означает, что треугольники ABL равнобедренный и его медиана LO является высотой, т. е. l перпендикулярна к а. Так как l ║ m и l перпендикулярна а, то m перпендикулярна а (по лемме о перпендикулярности двух параллельных прямых к третей). Итак, прямая а перпендикулярна к любой прямой m плоскости α, т. е. а перпендикулярна α.












 ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ Бозон Хиддинса
Бозон Хиддинса Трехгранный угол
Трехгранный угол Презентацию выполнила учитель ГБОУ СОШ №72 Андреева И.Ю.
Презентацию выполнила учитель ГБОУ СОШ №72 Андреева И.Ю. Смежные и вертикальные углы
Смежные и вертикальные углы Площади фигур. Зачёт
Площади фигур. Зачёт Сфера. Шар
Сфера. Шар Многообразие многоугольников
Многообразие многоугольников Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Отрезок. Длина отрезка
Отрезок. Длина отрезка Длина отрезка
Длина отрезка Площади и объемы
Площади и объемы Стереометрия в образах
Стереометрия в образах Сравнение величин углов. Классификация углов по градусной мере
Сравнение величин углов. Классификация углов по градусной мере Азбука геометрической резьбы
Азбука геометрической резьбы Задачи на готовых чертежах Четырехугольники Презентацию подготовила Команда «ЗВЕЗДОЧКИ» МКУО Тумановская СОШ Руководитель:
Задачи на готовых чертежах Четырехугольники Презентацию подготовила Команда «ЗВЕЗДОЧКИ» МКУО Тумановская СОШ Руководитель:  Задача о трисекции угла
Задача о трисекции угла Свойства пирамиды с равными боковыми ребрами
Свойства пирамиды с равными боковыми ребрами Прямоугольник и его свойства
Прямоугольник и его свойства Четырехугольники 9 класс
Четырехугольники 9 класс Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.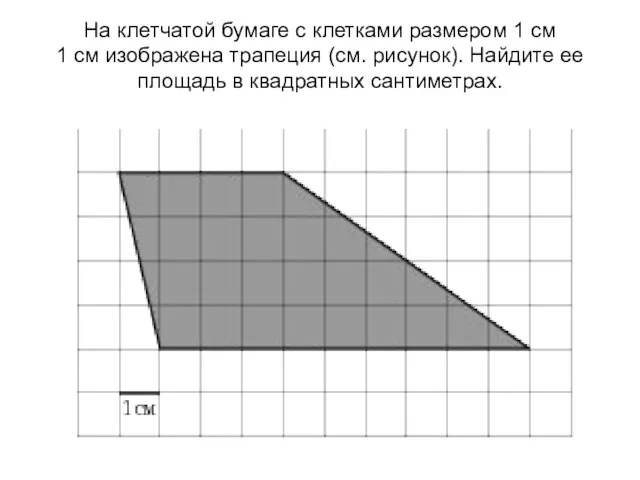 Площади фигур на клетке
Площади фигур на клетке Правильные выпуклые многогранники
Правильные выпуклые многогранники Сфера
Сфера Геометрия.Введение. Аксиоматика.
Геометрия.Введение. Аксиоматика. Амидекстр
Амидекстр Сечения многогранников плоскостью
Сечения многогранников плоскостью Пирамиды
Пирамиды