Слайд 4Изменение концентрации вещества А описывается линейным однородным дифференциальным уравнением 1-го порядка (1).

Начальным условиям соответствует уравнение (5) :
Поэтому, с учетом начального условия (5), можно написать следующее выражение для концентрации А: (6)
С учетом (6), дифференциальное уравнение для В преобразуется в
(7)
Дифференциальное уравнение (7) является неоднородным. Будем решать его методом вариации постоянной. Для этого надо сначала найти решение соответствующего однородного уравнения:
(8) (9)
где G – постоянная, которая при решении обычных однородных уравнений определяется из начальных условий. В методе вариации постоянной принимается, что G является функцией времени, G=G(t).
Слайд 5 (10)
Функцию G(t) находят, подставляя выражение (10) в неоднородное уравнение (7):

(11)
Находя производную левой части (11) по правилу дифференцирования произведения функций, получаем
(12)
Сокращая одинаковые слагаемые в левой и правой частях (12) , получаем:
(13)
Если k2 ≠ k1,
(14)
(15)
Слайд 6Подставляем полученное выражение (15) для G(t) в (10):
(16)
Постоянную интегрирования в (16)

определяем из начального условия [B] = 0 при t = 0
Получаем формулу зависимости концентрации В от времени:
(17)
С учетом уравнения материального баланса (4):
Слайд 7Таким образом, зависимости концентраций от времени для участников последовательной реакции дается следующими

выражениями:
(6)
(17)
(18)
Если k2 = k1 = k, то решение находится следующим образом:
Слайд 8
[A]0 = 1 М, [B]0 = 0, [Z]0 = 0. k1 =
![[A]0 = 1 М, [B]0 = 0, [Z]0 = 0. k1 =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/944749/slide-7.jpg)
1 мин-1, k2 = 0,4 мин-1
Слайд 9Рассмотрим приближенные выражения для концентрации промежуточного вещества В, которые получаются при условии,

что константа скорости второй реакции больше константы первой. Если k2 > k1, то, начиная с некоторого момента времени Т, будет выполняться неравенство exp(–k1t) >> exp(–k2t). Поэтому в выражении (17) мы можем пренебречь слагаемым exp(–k2t) по сравнению exp(–k1t). Получим:
Так как [A] = a· exp(–k1t) имеем: (19)
Если k2 >> k1, то в знаменателе (19) можно пренебречь k1 по сравнению с k2. Получим
(20)
Соотношения между концентрациями А и В, определяемые выражениями (19) и (20), называются переходным и вековым равновесиями соответственно.
Слайд 10
[A]0 = 1 М, [B]0 = 0, [Z]0 = 0. k1 =
![[A]0 = 1 М, [B]0 = 0, [Z]0 = 0. k1 =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/944749/slide-9.jpg)
1 мин-1, k2 = 4 мин-1
Слайд 11Метод квазистационарных концентраций

Слайд 12Зависимость концентрации промежуточного вещества от времени.
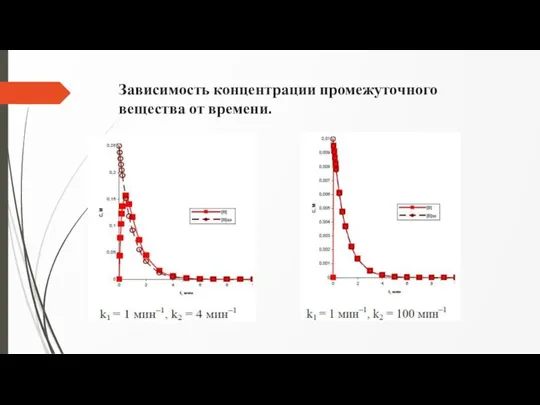






![[A]0 = 1 М, [B]0 = 0, [Z]0 = 0. k1 =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/944749/slide-7.jpg)

![[A]0 = 1 М, [B]0 = 0, [Z]0 = 0. k1 =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/944749/slide-9.jpg)


 Вычисление массовой доли химического элемента в веществе
Вычисление массовой доли химического элемента в веществе Презентация на тему Типы химических реакций на примере свойств воды
Презентация на тему Типы химических реакций на примере свойств воды  Презентация на тему Сахароза
Презентация на тему Сахароза  Смог як хімічне явище
Смог як хімічне явище Альдегиды
Альдегиды Структура материалов
Структура материалов Первые химические символы
Первые химические символы Развитие ассоциативного мышления на уроках химии
Развитие ассоциативного мышления на уроках химии Оксиды. Классификация и химические свойства
Оксиды. Классификация и химические свойства Металлы. Урок – обобщения
Металлы. Урок – обобщения Магматические горные породы
Магматические горные породы Презентация на тему Природные и синтетические красители и ароматизаторы
Презентация на тему Природные и синтетические красители и ароматизаторы  Уран гексафториді
Уран гексафториді Физические и химические явления в химии. Признаки химических реакций
Физические и химические явления в химии. Признаки химических реакций Тест по теме Альдегиды и кетоны
Тест по теме Альдегиды и кетоны Развитие энергетики и проблемы изменения структуры использования углеводородного сырья
Развитие энергетики и проблемы изменения структуры использования углеводородного сырья Исследование физико-химических свойств растворов сахарозы
Исследование физико-химических свойств растворов сахарозы Презентация на тему Таблица Менделеева и строение атома
Презентация на тему Таблица Менделеева и строение атома  Кислоты. Презентация к уроку химии в 8 классе
Кислоты. Презентация к уроку химии в 8 классе Эпоксидті полимер материалдарының қасиеттерін зерттеу
Эпоксидті полимер материалдарының қасиеттерін зерттеу Соли
Соли Введение в медицинскую химию: от молекулы к лекарству
Введение в медицинскую химию: от молекулы к лекарству Ковалентная полярная химическая связь
Ковалентная полярная химическая связь Презентация на тему Азотная кислота и ее соли (9 класс)
Презентация на тему Азотная кислота и ее соли (9 класс)  Основи масообміну
Основи масообміну Липиды
Липиды Коррозия металлов
Коррозия металлов Инновационное производство синтетических мелкокодисперсных оксидов и оборудования для их изготовления
Инновационное производство синтетических мелкокодисперсных оксидов и оборудования для их изготовления