Ангармоничность и колебательный спектр. Взаимодействия колебаний

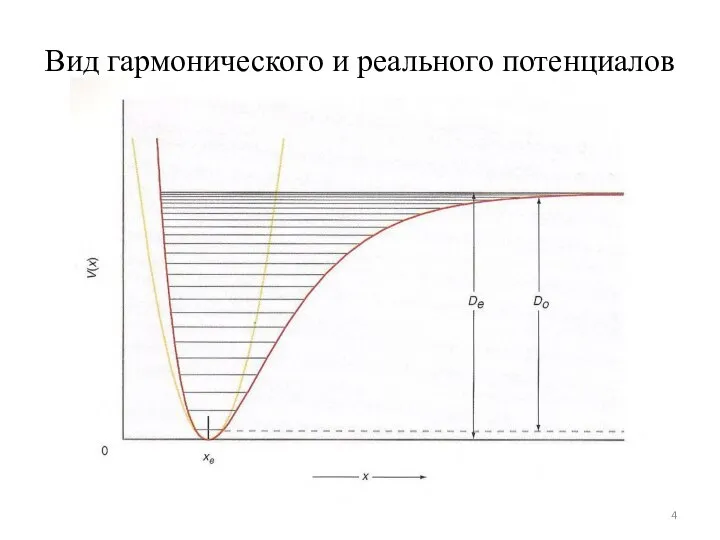
Вид гармонического и реального потенциалов

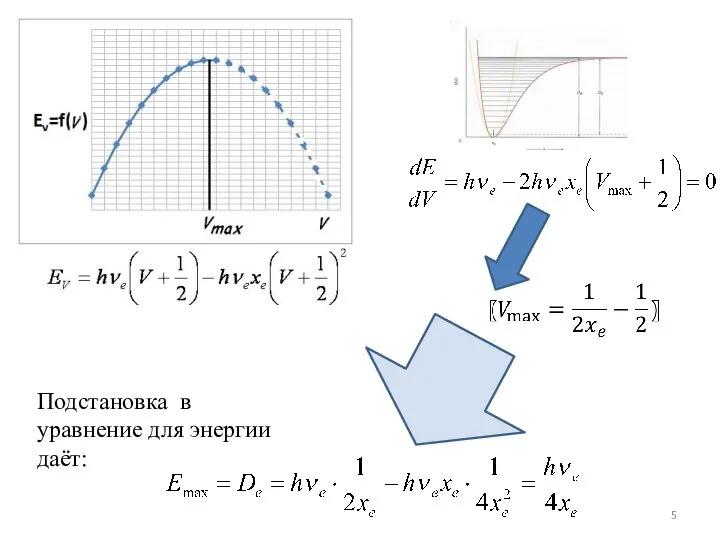
Подстановка в уравнение для энергии даёт:

Математически из этой формулы следует, что EV уменьшается при V > Vmax. Но физического смысла в этом нет, т.к. в этой области уравнение для EV уже не имеет смысла.

Пример
Для молекулы 1H35Cl полоса поглощения 2991 cm-1.
Рассчитайте силовую постоянную k.
Как изменится частота колебания, если водород заменить на дейтерий? (Силовая постоянная при этом не изменяется).
Решение
Запишем сначала .
Выражаем отсюда k:

b.
Частота колебания для DCl будет ниже.
Будет ли изотопический сдвиг таким же, если 37Cl заместить на 35Cl?
Высокая чувствительность к изотопическому замещению водорода на дейтерий делает ИК-спектроскопию эффективным способом определения атомов водорода в составе молекул.
В гармоническом приближении

Пример
Потенциал Морзе можно использовать для моделирования диссоциации. Молекула1H35Cl может быть описана с помощью этого потенциала с De=7,41·10-19 Дж. Силовая константа k для неё равна 516,3 Н/м и νe=8,97·1013 с-1.
Рассчитайте число разрешённых колебательных уровней и энергию связи в молекуле 1H35Cl.
Ответ: Vmax=24,4≈24

Решение

Обертоны и составные частоты
Пусть молекула содержит N атомов, тогда число возможных основных (фундаментальных) колебаний равно 3N – 5 – для линейной молекулы и 3N – 6 – для нелинейной формы.
Кроме основных колебаний в спектрах наблюдается ряд более слабых полос – обертонов и составных.
Под обертоном понимают полосы с частотами примерно кратными какой-либо основной полосе.
Составные частоты – это полосы, частота которых равна сумме или разности частот двух различных фундаментальных колебаний.

Взаимодействие колебаний

Взаимодействие колебаний в многоатомных молекулах
Пример: комплексы дифторидов бора
Область νBF2 .
В этой области отнесение полос можно сделать только на основании расчётов, учитывающих ММВ (т.е. в рамках моделей димеров и тетрамеров)
У комплекса F2B(AcAcH) группы BF2 (через атомы фтора) участвуют в двух типах статических нековалентных взаимодействий, а также в их спектрах обнаружились динамические взаимодействия (резонанс).

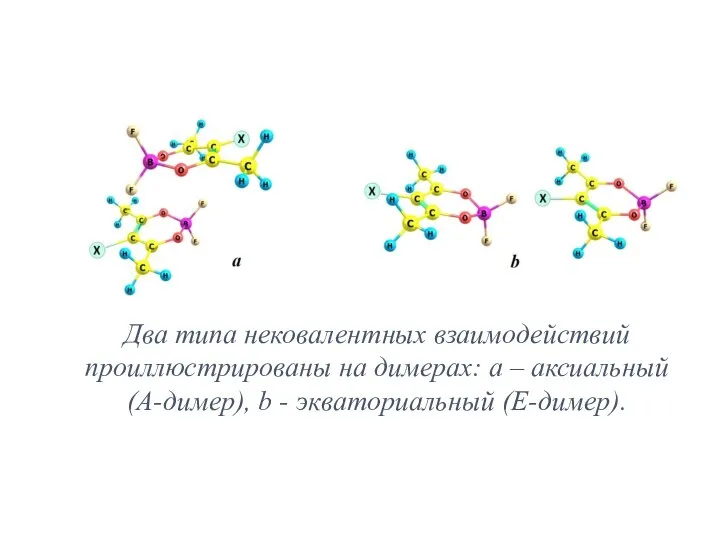
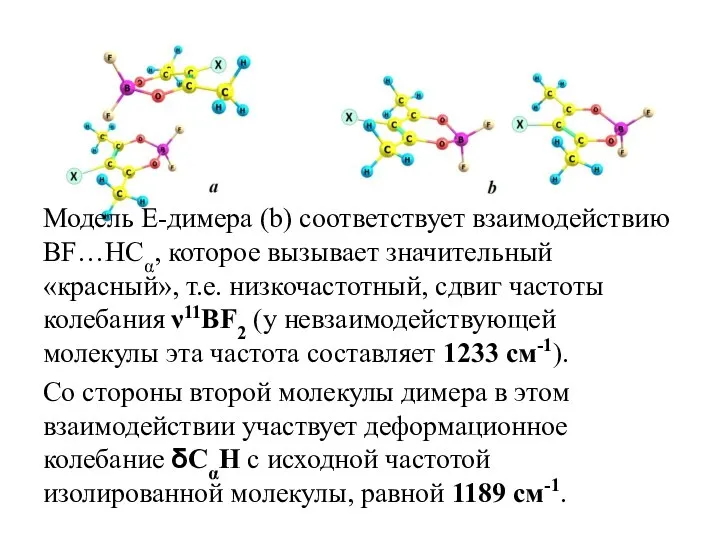
Два типа нековалентных взаимодействий проиллюстрированы на димерах: а – аксиальный (А-димер), b - экваториальный (Е-димер).

Модель E-димера (b) соответствует взаимодействию BF…HCα, которое вызывает значительный «красный», т.е. низкочастотный, сдвиг частоты колебания ν11BF2 (у невзаимодействующей молекулы эта частота составляет 1233 cм-1).
Со стороны второй молекулы димера в этом взаимодействии участвует деформационное колебание δCαH с исходной частотой изолированной молекулы, равной 1189 cм-1.

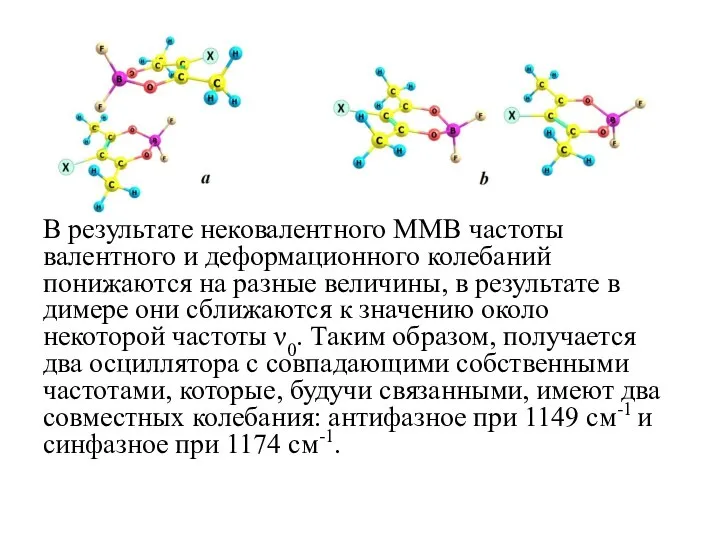
В результате нековалентного ММВ частоты валентного и деформационного колебаний понижаются на разные величины, в результате в димере они сближаются к значению около некоторой частоты ν0. Таким образом, получается два осциллятора с совпадающими собственными частотами, которые, будучи связанными, имеют два совместных колебания: антифазное при 1149 cм-1 и синфазное при 1174 cм-1.

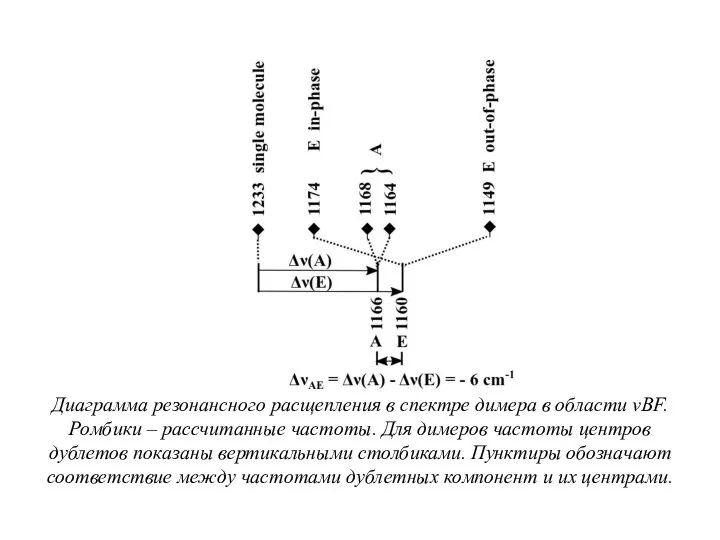
Диаграмма резонансного расщепления в спектре димера в области νBF. Ромбики – рассчитанные частоты. Для димеров частоты центров дублетов показаны вертикальными столбиками. Пунктиры обозначают соответствие между частотами дублетных компонент и их центрами.

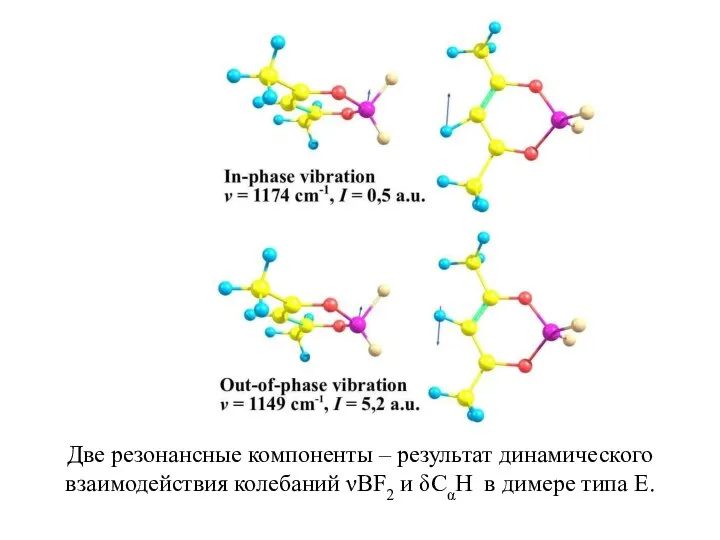
Две резонансные компоненты – результат динамического взаимодействия колебаний νBF2 и δСαН в димере типа Е.

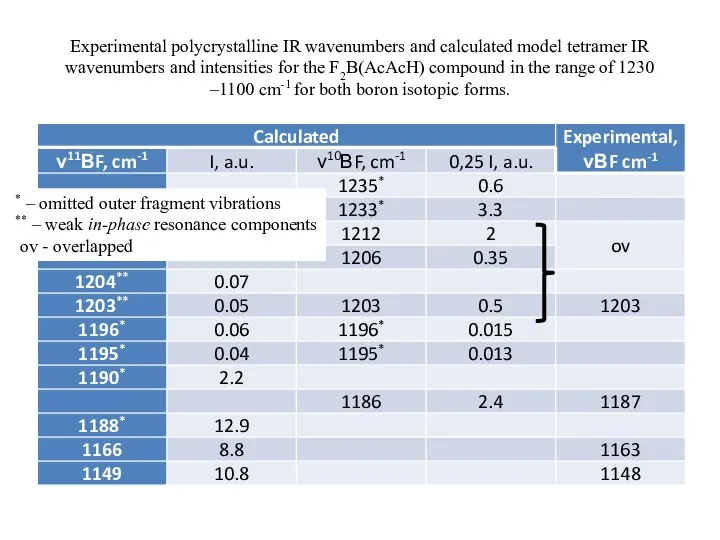
Experimental polycrystalline IR wavenumbers and calculated model tetramer IR wavenumbers and intensities for the F2B(AcAcH) compound in the range of 1230 –1100 cm-1 for both boron isotopic forms.
* – omitted outer fragment vibrations
** – weak in-phase resonance components
ov - overlapped

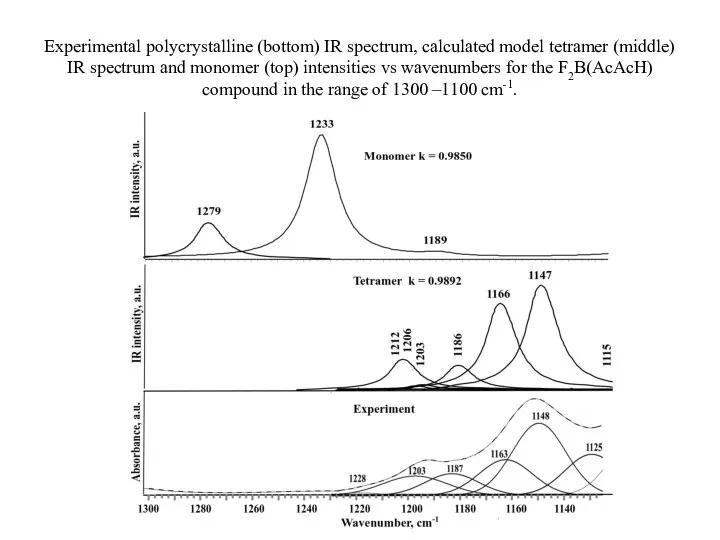
Experimental polycrystalline (bottom) IR spectrum, calculated model tetramer (middle) IR spectrum and monomer (top) intensities vs wavenumbers for the F2B(AcAcH) compound in the range of 1300 –1100 cm-1.

Резонанс Ферми
Резонанс Ферми — сильное взаимодействие между колебательными состояниями, возникающее, если двум колебательным состояниям в гармоническом приближении соответствуют одинаковые или почти одинаковые энергии (если не учитывать взаимное влияние). Явление было впервые объяснено известным итальянским физиком Энри́ко Фе́рми.

Объяснение расщепления симметричной частоты для молекулы CO2 было дано Ферми в 1931 г., впервые рассмотревшим взаимные возмущения колебательных уровней данного типа.

В инфракрасном спектре CO2 наблюдаются две очень интенсивные полосы
2349,3 см−1
и 667,3 см−1,
соответствующие разрешённым в ИК нечетным основным колебаниям А1u и E1u.

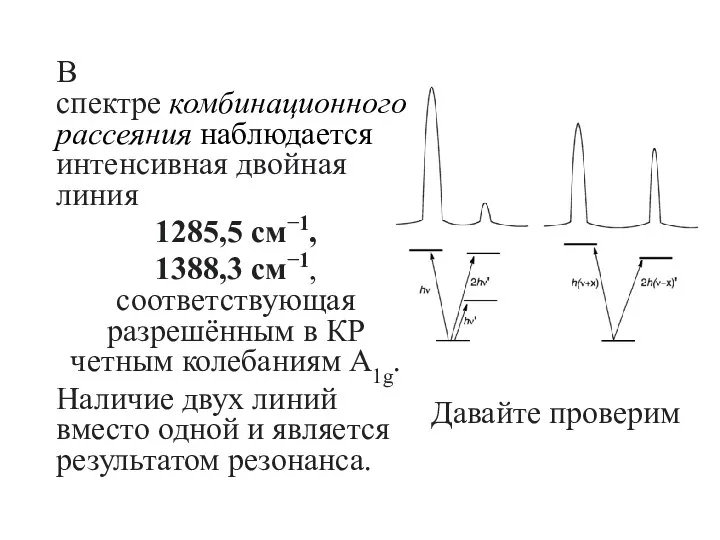
В спектре комбинационного рассеяния наблюдается интенсивная двойная линия
1285,5 см−1,
1388,3 см−1, соответствующая разрешённым в КР четным колебаниям А1g.
Наличие двух линий вместо одной и является результатом резонанса.
Давайте проверим

Если имеет место случайное вырождение, то благодаря взаимному влиянию колебаний — «возмущению» колебательных уровней — вырождение снимается и происходит расщепление вырожденного уровня, тем большее, чем сильнее взаимодействие.
В данном случае основная частота симметричного валентного колебания почти точно равна частоте первого обертона деформационного колебания.

Нулевые частоты равны ν1 = 1351,2 см−1 и ν2 = 672,2 см−1
(то есть 2ν2 ≈ ν1)
и вычисленные из них, с учетом ангармоничности колебаний, положения уровней разнятся лишь на 6,8 см−1.
Вследствие взаимодействия колебаний ν1 и 2ν2 расстояние между уровнями увеличивается до 1388,3 — 1285,5 = 102,8 (см−1),
и вместо интенсивной основной частоты ν1 и слабого обертона 2ν2 получаются две интенсивные полосы, каждая из которых соответствует смешиванию обоих колебаний.

Хотя резонанс Ферми и является результатом случайного вырождения, однако встречается довольно часто, особенно у сложных молекул;
из-за большого числа различных обертонов и составных частот вероятность случайных совпадений колебательных уровней достаточно велика.

Пример из студенческой работы 2017 года
В спектре ацетокси-замещённого комплекса полоса основного тона ν1 находится при 1776 см-1 и соответствует валентному колебанию связи CcaOca, а полоса ν2 – родительского колебания для обертона 2ν2 наблюдается при 891 см-1 и соответствует смешанному колебанию, в состав которого входят изменения длин связей CcaOα и CcaCmα и плоская деформация ацетокси. Для этих полос наблюдается резонанс Ферми.

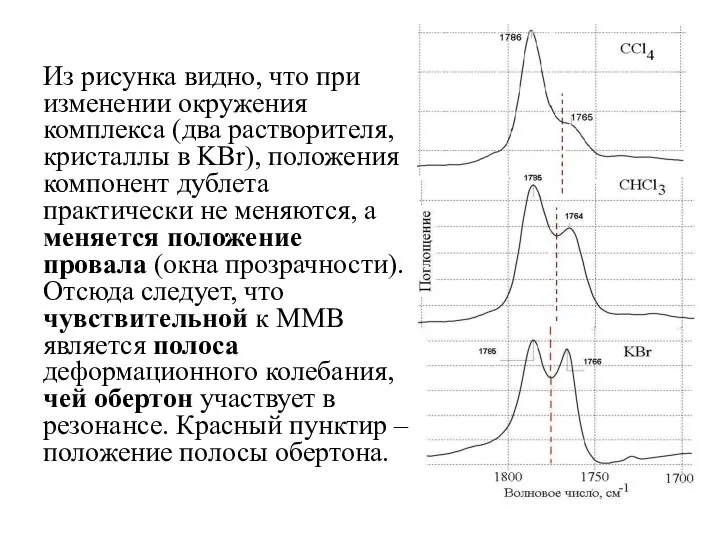
Из рисунка видно, что при изменении окружения комплекса (два растворителя, кристаллы в KBr), положения компонент дублета практически не меняются, а меняется положение провала (окна прозрачности). Отсюда следует, что чувствительной к ММВ является полоса деформационного колебания, чей обертон участвует в резонансе. Красный пунктир – положение полосы обертона.

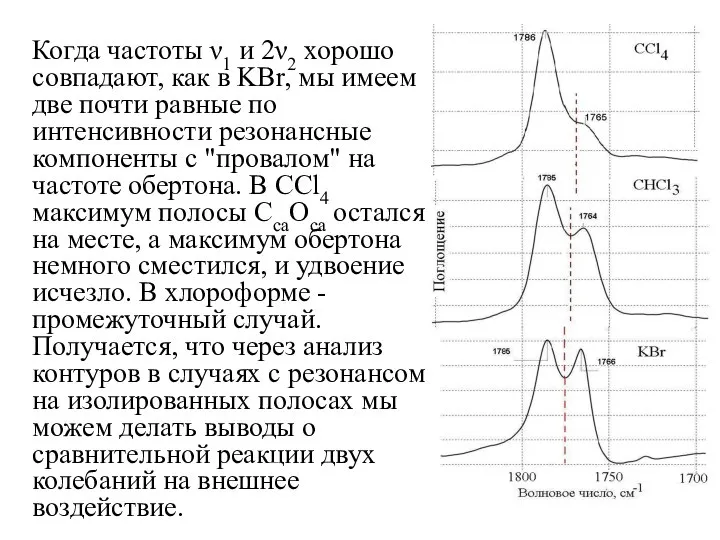
Когда частоты ν1 и 2ν2 хорошо совпадают, как в KBr, мы имеем две почти равные по интенсивности резонансные компоненты с "провалом" на частоте обертона. В СCl4 максимум полосы CcaOca остался на месте, а максимум обертона немного сместился, и удвоение исчезло. В хлороформе - промежуточный случай. Получается, что через анализ контуров в случаях с резонансом на изолированных полосах мы можем делать выводы о сравнительной реакции двух колебаний на внешнее воздействие.

Расстояние между максимумами отражает силу резонанса, чем он сильнее, тем больше расщепление.
Важнейшим следствием резонанса Ферми для экспериментатора является то, что обертон, интенсивность которого до взаимодействия была очень мала, сравнивается по интенсивности с основным тоном и его полоса становится заметной.