Слайд 2Попытки кинетического обобщения термодинамики делались с начала XX в. Начиная с работ

ОнзагераПопытки кинетического обобщения термодинамики делались с начала XX в. Начиная с работ Онзагера (1931 г.) можно уже говорить о систематическом построении новой термодинамики необратимых процессов, интенсивно развиваемой в настоящее время.
Основными постулатами этой теории, применимыми лишь к небольшим отклонениям от равновесия, являются:
1) утверждение о линейной зависимости 1) утверждение о линейной зависимости обобщенных термодинамических потоков от обобщенных потенциалов
2) соотношение Онзагера2) соотношение Онзагера, выражающее равенство перекрестных коэффициентов этой зависимости
3) теорема Пригожина о минимальности производства энтропии.
Слайд 3Термодинамика необратимых процессов Онзагера имеет в своей основе весь аппарат классической термодинамики,

включая первое и второе начала, а также два дополнительных принципа – линейности и взаимности . Принцип линейности возник на основе обобщения известного уравнения , описывающего процесс распространения теплоты в анизотропном кристалле, на любые разнородные явления. Идея взаимности почерпнута из соотношений взаимности .
Слайд 4Для доказательства теоремы взаимности Онзагер воспользовался принципом микроскопической обратимости из теории детального

равновесия химических реакций. Он распространил этот принцип на неравновесные системы, находящиеся вблизи состояния равновесия, и таким образом доказал справедливость соотношений
Слайд 5За свою работу Онзагер в 1968 г. был удостоен Нобелевской премии. Эта

награда подчеркивает важность для науки того факта, что теория, наконец, повернулась лицом к реальным необратимым процессам; она несомненно привлечет внимание инженеров и исследователей к идеям термодинамики, отличающимся фундаментальностью и неисчерпаемыми возможностями.
Слайд 6Первый постулат Онзагера дает объяснение ряду таких используемых в технике процессов, как

термодиффузия, термоэлектричество и др. В указанных примерах наличие «чужой» термодинамической движущей силы — градиента температуры — приводит соответственно к переносу компонентов и возникновению разности электрического потенциала.
Слайд 7Вторым положением термодинамики необратимых процессов Онзагер постулировал связь между термодинамической характеристикой системы

— энтропией, скоростью протекания необратимых процессов и термодинамическими движущими силами.
В соответствии со вторым постулатом Онзагера произведение абсолютной температуры на прирост локальной энтропии в единицу времени за счет протекания необратимых процессов (скорость возникновения, генерация энтропии) равно сумме произведений плотности потока на «собственную» термодинамическую движущую силу:
Важность второго постулата Онзагера заключается в том, что он связывает термодинамическую характеристику системы - энтропию — со скоростью протекания процессов, которую не рассматривает классическая термодинамика.
Слайд 8Следующий вывод можно сделать из результатов предыдущего раздела. Мы получили для случая

одной химической реакции выражения для кинетических коэффициентов в явном виде . Из этой матрицы следует, что Lik = Lki.
Оказывается, это соотношение выполняется всегда. Оно называется правилом симметрии кинетических коэффициентов. Это правило для общего случая не может быть получено в рамках термодинамики, поэтому Онзагер ввел его в качестве третьего постулата термодинамики необратимых процессов. Физический смысл этого постулата может быть понят только с помощью статистической термодинамики. Можно показать, что он является следствием так называемой микроскопической обратимости, т.е. инвариантности уравнений механики (как классической, так и квантовой) по отношению к изменению знака времени. Иначе говоря, третий постулат следует из того факта, что если повернуть время вспять, то микрочастицы будут двигаться в обратном направлении, но по тем же траекториям.
Слайд 9В заключение еще раз подчеркнем, что в сложных энерготехнологических процессах вопросы математического

моделирования тепломассопереноса тесно связаны с рассмотрением физико-химических процессовВ заключение еще раз подчеркнем, что в сложных энерготехнологических процессах вопросы математического моделирования тепломассопереноса тесно связаны с рассмотрением физико-химических процессов. В последнее время при рассмотрении физико-химических процессовВ заключение еще раз подчеркнем, что в сложных энерготехнологических процессах вопросы математического моделирования тепломассопереноса тесно связаны с рассмотрением физико-химических процессов. В последнее время при рассмотрении физико-химических процессов и анализе динамическогоВ заключение еще раз подчеркнем, что в сложных энерготехнологических процессах вопросы математического моделирования тепломассопереноса тесно связаны с рассмотрением физико-химических процессов. В последнее время при рассмотрении физико-химических процессов и анализе динамического поведения сложных нелинейных систем все большее внимание уделяется вопросам неравновесной термодинамики .








 Получение галогенов. Биологическое значение и применение галогенов и их соединений
Получение галогенов. Биологическое значение и применение галогенов и их соединений Абсорбционная осушка газа
Абсорбционная осушка газа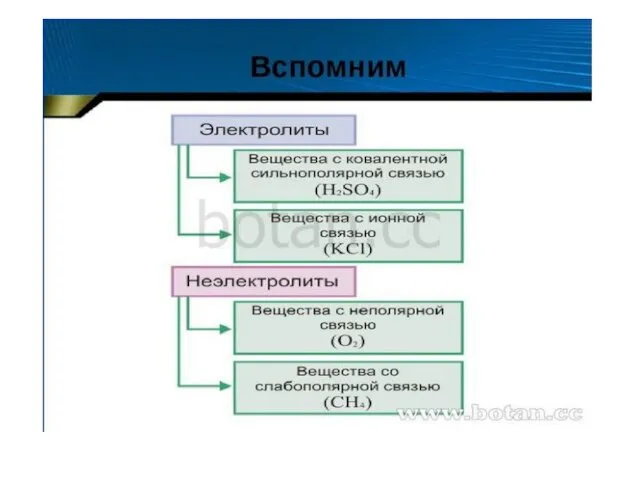 Диссоциация веществ
Диссоциация веществ Добыча золота в России По теме «Внешние эффекты и права собственности»
Добыча золота в России По теме «Внешние эффекты и права собственности» Компетентностный подход в обучении химии "Плохой учитель преподносит истину, хороший учит ее находить» А. Дист
Компетентностный подход в обучении химии "Плохой учитель преподносит истину, хороший учит ее находить» А. Дист Химическая кинетика и равновесие
Химическая кинетика и равновесие Метаболизм липидов
Метаболизм липидов Вуглеводи
Вуглеводи Биологическая роль III(A) группы
Биологическая роль III(A) группы Введение в дисциплину Процессы и аппараты химической технологии
Введение в дисциплину Процессы и аппараты химической технологии Полиморфизм. Аллотропия
Полиморфизм. Аллотропия Зависимость скорости от температуры
Зависимость скорости от температуры Подготовка к контрольной работе по теме «Изменения, происходящие с веществами
Подготовка к контрольной работе по теме «Изменения, происходящие с веществами Предельные одноатомные спирты: свойства, получение, применение
Предельные одноатомные спирты: свойства, получение, применение Алканы
Алканы Металлы
Металлы Геохимический анализ поверхностных вод Звенигородской биостанции
Геохимический анализ поверхностных вод Звенигородской биостанции Презентация Лекция 2. Химическая кинетика
Презентация Лекция 2. Химическая кинетика Вчення про розчини. Колігативні властивості розчинів
Вчення про розчини. Колігативні властивості розчинів Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс)  Презентация на тему Микроэлементы: Хром, Йод, Фтор
Презентация на тему Микроэлементы: Хром, Йод, Фтор  Химия. Электролитическая диссоциация. (9 класс)
Химия. Электролитическая диссоциация. (9 класс) Оксиды азота
Оксиды азота Презентация на тему Полисахариды. Крахмал и целюлоза
Презентация на тему Полисахариды. Крахмал и целюлоза  Химическая коррозия
Химическая коррозия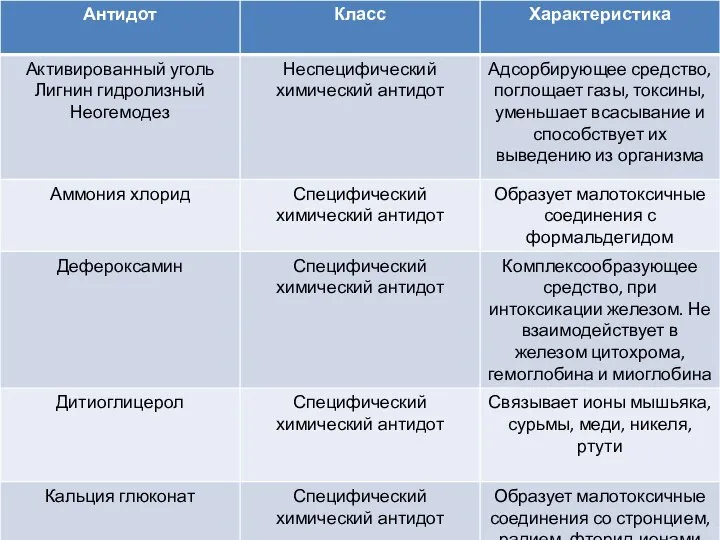 Антидоты. Класс. Характеристика
Антидоты. Класс. Характеристика Виробництво 4-амінофенолу потужністю 670 т/рік з розробкою стадії відновлення
Виробництво 4-амінофенолу потужністю 670 т/рік з розробкою стадії відновлення Школа юных ученых. Соль
Школа юных ученых. Соль