Содержание
- 2. В дисциплине представлены теоретические представления об основных процессах переработки полимеров: смешение, экструзия, вальцевание, каландрование, литье под
- 3. В области переработки полимеров можно выделить четыре основных направления. 1. Приготовление композиций, обладающих свойствами, отличными от
- 4. 3. Изготовление изделий из термореактивных материалов (СРТТ). Окончательное формирование химической структуры этих материалов происходит на нескольких
- 5. Задача экспериментального установления оптимума по комплексу параметров технологического процесса потребует длительных экспериментов. Вследствие большой производительности современного
- 6. Уникальные деформационные свойства полимеров, обусловливающие возможность их широкого применения, определяются длиной и подвижностью макромолекул. В данном
- 7. В результате многочисленных исследований установлено, что основная осо-бенность расплавов полимеров и эластомеров заключается в существовании аномалии
- 8. Строгая постановка задачи часто оказывается практически невозможной, и при математическом описании реальных производственных процессов приходится прибегать
- 9. Для грамотного описание процесса смешения необходимы и представления о механизме плавления полимера. Плавление полимера в канале
- 10. Каландрование полимеров во много подобно вальцеванию. Поэтому его изотермическая модель в принципе не отличается от модели
- 11. ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ О МОЛЕКУЛЯРНОЙ И НАДМОЛЕКУЛЯРНОЙ СТРУКТУРЕ ПОЛИМЕРОВ Полимерные материалы отличаются от металлов, стекла или камня,
- 12. Для наглядного подтверждения основных положений была создана физическая модель линейной макромолекулы, увеличенной в 25 млн. раз,
- 13. Отсутствие в представленной модели сил межмолекулярного взаимодействия ограничивает применимость такой модели областью сильноразбавленных растворов полимеров. Однако
- 14. Длинные и гибкие макромолекулы, способные как к свернутым, так и к выпрямленным конформациям, образуют и выпрямленные
- 15. г) сферолиты — крупные структурные образования, построенные из пачек и фибрилл; эти структуры характерны для кристаллизующихся
- 16. Кристаллические полимеры Наиболее часто при медленной кристаллизации возникают фибриллярные кристаллы, которые имеют форму длинных лент. Ширина
- 17. Переход от кристаллической к аморфной фазе в полимерах осуществляется постепенно, через ряд промежуточных форм. Эти формы
- 18. ДЕФОРМАЦИОННЫЕ СВОЙСТВА ПОЛИМЕРОВ В ЗАВИСИМОСТИ ОТ ТЕМПЕРАТУРЫ Температура оказывает сильное влияние на механические свойства полимеров, поскольку
- 19. Фазовые состояния полимера В термодинамике различают: - кристаллические, - жидкие - газовые фазы, отличающиеся друг от
- 20. Некоторые термины, понятия и определения ТЕМПЕРАТУРА ТЕКУЧЕСТИ (fluidity temperaturе Tf ) - температура, при которой полимер
- 21. Аморфные вещества, как правило, не обладают чёткой температурой плавления ростом температуры снижается вязкость таких веществ, и
- 22. ТЕРМОМЕХАНИЧЕСКИЕ КРИВЫЕ – КАК МЕТОД ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ФАЗОВОГО СОСТОЯНИЯ Один из наиболее простых методов изучения температурной
- 23. Типичная термомеханическая кривая аморфного полимера - на рисунке. По этой кривой можно довольно четко выделить температурные
- 24. Температурные переходы. Способы графического определения температур фазовых переходов. Ширина области температурного перехода может составлять 20 —
- 25. Кристаллические полимеры Типичные термомеханические кривые для кристаллических полимеров представлены на рисунке. Ряд кристаллических полимеров способен плавится
- 26. I участок - стеклообразное состояние; в тепловом движении участвуют атомы или группы атомов, совершающие колебательные движения
- 27. Структурное стеклование.Под действием теплового движения, узлы сетки распадаются в одном месте и возникают в другом. С
- 28. Факторы, влияющие на температуру структурного стеклования: - скорость охлаждения; - гибкость цепи полимера (интенсивность внутри- и
- 29. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУР ФАЗОВЫХ ПЕРЕХОДОВ ПОЛИМЕРОВ МЕТОДАМИ ТЕРМИЧЕСКОГО АНАЛИЗА Дифференциальный термический анализ (ДТА) — метод исследования, заключающийся
- 31. Дифференциальная сканирующая калориметрия (ДСК) – Термоаналитическая методика, в которой разница в количестве тепла, необходимого для повышения
- 32. ОСНОВНЫЕ ВИДЫ ДЕФОРМАЦИИ Почти все полимерные материалы в определенном температурном интервале способны к большим частично обратимым
- 33. Рассмотрим призму длиной l0, к торцу которой приложено растягивающее напряжение σ0. Предположим, что материал призмы подчиняется
- 34. Упругая и пластическая деформация Рассмотрим деформацию элементарной призмы, к верхней и нижней поверхностям которой приложена тангенциальная
- 35. ДИАГРАММА НАПРЯЖЕНИЕ — ДЕФОРМАЦИЯ Термомеханическая кривая описывает механические свойства полимеров при малых деформациях. В большинстве случаев
- 36. Семейство типичных диаграмм растяжения аморфного полимера в координатах условное напряжение — деформация, определенных при различных температурах,
- 37. Вынужденная высокоэластическая деформация Молекулярный механизм развития вынужденно-эластической деформации в основном идентичен механизму обычной высокоэластической деформации и
- 38. Кристаллические полимеры Диаграммы растяжения кристаллических полимеров очень похожи на диаграммы растяжения аморфных в застеклованном состоянии. При
- 39. РЕЛАКСАЦИОННЫЕ ЯВЛЕНИЯ ПРИ ДЕФОРМАЦИИ ПОЛИМЕРОВ Процесс деформации — это процесс изменения конформации макромолекул под действием поля
- 40. Динамический механический анализ (ДМА) Применяется для исследований зависимости механических и вязкоупругих свойств материалов от температуры, времени
- 41. Теория Инструменты ДМА прилагают колебательную силу (напряжение) и регистрируют осциллирующее изменение образца. Модуль упругости рассчитывается исходя
- 43. ОСОБЕННОСТИ ТЕЧЕНИЯ ПОЛИМЕРОВ У большинства жидкостей коэффициент вязкости η зависит только от при-роды жидкости и температуры.
- 44. Графически можно изобразить закон Ньютона прямой с угловым коэффициентом, равным 1/η (прямая 1). Существует большой класс
- 45. Тело Максвелла. Представления об упругости материала, полностью подчиняющегося закону Гука, и вязкой жидкости, удовлетворяющей закону Ньютона,
- 46. Если подвергнуть тело Максвелла деформации, приложив к нему постоянное усилие, то можно ожидать, что сначала образец
- 47. Аналитическое уравнение деформации модели Дифференцирование уравнение по времени: Величина dγy /dt (упругая часть) может быть определена
- 48. Классификация жидкостей Существует следующая классификация жидкостей по зависимости вязких напряжений от скорости сдвига: Ньютоновская жидкость —
- 49. Опыт показывает, что большинство полимеров и их растворов в условиях переработки обладает аномалией вязкости, что сильно
- 50. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ТЕРМОДИНАМИКИ И ТЕПЛОПЕРЕДАЧИ, ПРИМЕНЯЕМЫЕ ПРИ ОПИСАНИИ ПРОЦЕССОВ ПЕРЕРАБОТКИ ПОЛИМЕРОВ Практически все процессы переработки полимеров
- 51. Механическая работа, совершаемая в обратимом процессе расширения или сжатия, определяется уравнением: dW = P·dV , где
- 52. УРАВНЕНИЕ СОСТОЯНИЯ Уравнение, описывающее изменение удельного объёма в зависимости от основных термодинамических параметров — температуры и
- 53. Термодинамическое уравнение состояния Классическая термодинамика, используя представление о связи давления с изменением внутренней энергии и энтропии,
- 54. Уравнение состояния Спенсера–Джилмора (Spencer-Gilmore equation) Пытаясь обобщить известные экспериментальные данные по сжимаемости и температурному расширению расплавов
- 55. ТЕПЛООБМЕН Различают три вида теплообмена: теплопроводность, теплопередача конвекцией лучистый теплообмен. Передача тепла за счёт теплопроводности осуществляется
- 56. ТЕПЛОПРОВОДНОСТЬ Основной задачей теории теплопроводности является установление распределения температур внутри тела. Передача тепла происходит во всех
- 57. Теплопередача в стационарном режиме. Теплопередачу в непрерывно действующих нагревательных системах перерабатывающего оборудования можно рассматривать как независящую
- 58. ТЕПЛОПЕРЕДАЧА В ПОТОКАХ РАСПЛАВА Передача тепла в движущейся жидкости происходит по механизму конвективного теплообмена, который осуществляется
- 59. Использование методов теории подобия позволяет свести решение проблемы теплообмена в потоке жидкости к экспериментальному определению вида
- 60. Известные в настоящее время результаты экспериментального исследования теплообмена в расплавах полимеров относятся преимущественно к течению в
- 61. ЛУЧИСТЫЙ ТЕПЛООБМЕН Лучистая энергия передается в виде электромагнитных волн, распростра-няющихся в пространстве до тех пор, пока
- 62. При расчете лучистого теплообмена между чёрными телами под излучение попадает только та часть тела, которая просматривается
- 63. СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ О МЕХАНИЗМЕ СТРУКТУРООБРАЗОВАНИЯ В ПРОЦЕССАХ ПЕРЕРАБОТКИ ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ КИНЕТИКИ КРИСТАЛЛИЗАЦИИ Из теории изотермической кристаллизации
- 64. Образование упорядоченных структур благодаря более компактной упаковке сопро-вождается одновременным уменьшением удельного объема. Поэтому для изучения временной
- 65. Обычно в качестве характеристики температурной зависимости константы скорости кристаллизации используют значения не самой константы, а величину
- 66. ВЛИЯНИЕ ТЕМПЕРАТУРЫ И СКОРОСТИ ОХЛАЖДЕНИЯ НА КРИСТАЛЛИЗАЦИЮ
- 68. Скачать презентацию
Слайд 2 В дисциплине представлены теоретические представления об основных процессах переработки полимеров:
смешение,
экструзия,
вальцевание,
В дисциплине представлены теоретические представления об основных процессах переработки полимеров:
смешение,
экструзия,
вальцевание,

каландрование,
литье под давлением,
прокатка,
раздув.
Математические модели процессов построены с учётом специфики физических свойств полимеров, влияющих на основные технологические характеристики процесса. Особое внимание уделено связи между физическими параметрами процесса переработки, механизмом формирования надмолекулярных структур и эксплуатационными характеристиками готовых изделий.
Переработка полимерных материалов — это совокупность технологических приёмов, методов и процессов, посредством которых исходный полимер превращают в различные изделия с заданными эксплуатационными характеристиками.
Слайд 3
В области переработки полимеров можно выделить четыре основных направления.
1. Приготовление композиций,
В области переработки полимеров можно выделить четыре основных направления.
1. Приготовление композиций,

В настоящее время создание композиций — это целая отрасль промышленности переработки полимеров. Введение стабилизаторов, пластификаторов, антиоксидантов, наполнителей, специальных добавок стало неотъемлемой частью процесса производства полимерных материалов.
2. Изготовление изделий из термопластичных материалов (БП и Т и СТ, изготавливаемые по баллиститной технологии).
При этом протекают следующие основные процессы:
а) плавление материала;
б) пластическая деформация материала, в результате которой вязкой массе придается конфигурация будущего изделия;
в) охлаждение материала до температуры теплостойкости, при которой может сохраняться приданная ему форма.
В ряде случаев процессу формования сопутствуют процессы механической ориентации, обеспечивающей улучшение прочностных характеристик материала.
Слайд 4
3. Изготовление изделий из термореактивных материалов (СРТТ). Окончательное формирование химической структуры
3. Изготовление изделий из термореактивных материалов (СРТТ). Окончательное формирование химической структуры

а) нагрев материала до перехода в вязкопластическое состояние;
б) пластическая деформация материала, в процессе которой в него вводятся необходимые дополнительные ингредиенты;
в) полученную в процессе смешения композицию вновь подвергают пластической деформации для придания ей формы готового изделия;
г) нагрев готового изделия до температуры отверждения (вулканизации, полимери-зации), при которой в материале протекают химические реакции, обеспечивающие образование непрерывной пространственной поперечной структуры.
4. Изготовление изделий непосредственно из мономеров. При переработке этим методом реакция полимеризации протекает непосредственно в форме, и процесс образования полимера оказывается совмещенным с процессом формирования готового изделия.
В настоящее время в промышленности переработки полимеров более широко представлены первые три направления. Вследствие этого наиболее глубоко разработаны соответствующие технологические процессы и методы их теоретического описания.
Слайд 5 Задача экспериментального установления оптимума по комплексу параметров технологического процесса потребует длительных экспериментов.
Задача экспериментального установления оптимума по комплексу параметров технологического процесса потребует длительных экспериментов.

Вследствие большой производительности современного перерабатывающего оборудования и высокой стоимости технологических линий проведение эксперимен-тальных исследований реального процесса переработки полимеров, превращается в дорогостоящую и продолжительную работу. Поэтому целесообразно изучать особенность каждого конкретного процесса, рассматривая вначале его теоретическое описание, т. е. его математическую модель.
Физическому эксперименту всегда предшествует этап теоретического эксперимента.
На этом этапе нет необходимости прибегать к реальным экспериментам, вместо этого исследуются количественные характеристики процесса, полученные расчетным методом. Такой подход позволяет существенно снизить объем физического эксперимента, поскольку прибегать к нему приходится на самой последней стадии — не в процессе поиска основных закономерностей, а для проверки и уточнения выданных рекомендаций.
Для того чтобы исследуемые теоретические модели процессов описывали процессы с достаточно хорошим приближением, они непременно должны учитывать основные особенности моделируемых явлений.
Слайд 6 Уникальные деформационные свойства полимеров, обусловливающие возможность их широкого применения, определяются длиной и
Уникальные деформационные свойства полимеров, обусловливающие возможность их широкого применения, определяются длиной и

В данном курсе будут рассмотрены основные закономерности, связывающие молекулярную и надмолекулярную структуры полимера с его деформационными характеристиками.
Приведен анализ физической сущности релаксационных явлений и методов их количественного описания. Будет рассмотрена природа высокоэластических деформаций.
Особое внимание уделено введению основных понятий таких, как упругая, высокоэластическая и пластическая деформация, скорость сдвига, релаксационный и динамический модули.
Механические свойства полимерных материалов в значительной мере зависят от характера надмолекулярных структур, формирующихся в процессе пере-работки. По мере развития теории процессов переработки полимеров было установлено, что для правильного определения основных параметров технологического процесса большое значение имеют сведения о деформационных характеристиках расплава полимера, полученные в широком интервале температур и скоростей деформации. Зависимости такого рода получают экспериментально при реологических исследованиях полимеров.
Реология полимеров, сравнительно молодая область физики полимеров, возникшая в 20-х годах прошлого века, в настоящее время превратилась в самостоятельную науку.
Слайд 7 В результате многочисленных исследований установлено, что основная осо-бенность расплавов полимеров и эластомеров
В результате многочисленных исследований установлено, что основная осо-бенность расплавов полимеров и эластомеров

В отличие от обычных вязких жидкостей, деформационные свойства которых можно охарактеризовать одной физической константой — (ньютоновской) вязкостью, для характеристики вязкостных свойств расплавов полимеров приходится прибегать к многопараметрическим зависимостям. Это обстоятельство не только осложняет технику экспериментального определения вязкостных свойств расплавов, но и существенно усложняет математический аппарат, используемый в теории переработки.
Анализ физической сущности большинства процессов переработки термо-пластичных и термореактивных материалов показывает, что физические явления (диссипативный разогрев, ориентация, механокрекинг и т. д.) возникают вследствие деформации полимерной среды. Поэтому при построении теории переработки , основным является создание методов количественного описания механики процессов переработки, с учётом главных особенностей полимерного материала.
Всё многообразие известных процессов переработки можно было бы отождествить с набором отдельных задач, отличающихся друг от друга только начальными и гранич-ными условиями.
Каждая из таких задач должна содержать: уравнения движения сплошной среды, записанные в той или иной форме, уравнение материального баланса,
уравнение энергетического баланса и реологическое уравнение состояния, характеризующее сопротивляемость среды приложенным к ней внешним воздействиям
Слайд 8 Строгая постановка задачи часто оказывается практически невозможной, и при математическом описании реальных
Строгая постановка задачи часто оказывается практически невозможной, и при математическом описании реальных

Приём такого рода вполне допустим. Он позволяет независимо устанавливать основные закономерности наиболее простых случаев одномерного изотермического течения псевдопластичных жидкостей, выбранных в качестве математического аналога полимерных расплавов.
Термодинамические соотношения и закономерности теплопередачи, описыва-ющие разогрев и плавление полимеров, являются фундаментом, на базе которого строятся неизотермические модели реальных процессов переработки. Установлено влияние ориентации расплава на кинетику процесса кристаллизации и характер возникающих надмолекулярных структур.
Смешение в той или иной мере происходит почти во всех процессах перера-ботки полимеров. Получение расплава с однородной температурой — одна из основных задач: применение смесительных насадок, торпед и другие различные приемы увеличения эффективности смешения.
Таким образом, перед построением модели каждого технологического процесса ознакомимся с их физическую сущность.
Такой подход необходим, потому что при построении математических моделей крайне важно правильно выбирать степень адекватности модели реальному явлению, избегая как чрезмерного упрощения, так и чрезмерного усложнения.
Слайд 9 Для грамотного описание процесса смешения необходимы и представления о механизме плавления полимера.
Для грамотного описание процесса смешения необходимы и представления о механизме плавления полимера.

Плавление полимера в канале напоминает плавление толстой пластины, одна поверхность которой скользит по горячему металлическому листу. При этом слой расплава, образовавшийся на поверхности пластины, соскребается скребком в одну сторону. Появление моделей процессов плавления позволило приступить к построению математической модели всего процесса экструзии.
В настоящее время все основные параметры процесса экструзии могут быть рассчитаны, если известны характеристики полимера, температура корпуса.
Для изучения процесса вальцевания подробно рассмотрено движение вязкой жидкости в пространстве между двумя вращающимися валками. Анализ качественной картины движения жидкости позволяет понять природу циркуляционного течения и объяснить смесительное воздействие, которому подвергается перерабатываемый материал.
Наиболее простая модель основана на качении твердого цилиндра по слою вязкой ньютоновской жидкости. Более точная модель вальцевания строится с учётом ано-малии вязкости. Такая модель не даёт строгого количественного описания процес-са, но весьма полезна для выбора технологических параметров вальцевания.
Оценка смесительного воздействия сделана применительно к течению ньюто-новской* жидкости. Однако даже такое приближение позволяет ввести в качестве меры смесительного воздействия значение удельной деформации сдвига, хорошо коррелирующей с эксплуатационными характеристиками изделий.
_______________________________________________
* Исаак Ньютон (Isaac Newton 1643 - 1727) — английский физик, математик, механик, астроном; один из создателей классической физики
Слайд 10 Каландрование полимеров во много подобно вальцеванию. Поэтому его изотермическая модель в принципе
Каландрование полимеров во много подобно вальцеванию. Поэтому его изотермическая модель в принципе

Литье под давлением - это наиболее распространенный в настоящее время метод изготовления изделий из термопластичных и термореактивных полимеров еще не имеет полного математического описания. Качественная картина процесса довольно хорошо известна. Процесс состоит из двух этапов:
приготовление порции расплава, необходимой для формования изделия, и впрыск ее в холодную форму;
2) охлаждение расплава до температуры теплостойкости и извлечение готового изделия.
Анализ процесса охлаждения литых изделий выполнен в предположении постоянства значений теплофизических свойств полимера во всем интервале температур охлаждения. Несмотря на очевидную приближенность этого допущения, сопоставление результатов расчета с продолжительностью реальных циклов охлаждения всегда давало удовлетворительные результаты.
Слайд 11ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ О МОЛЕКУЛЯРНОЙ И НАДМОЛЕКУЛЯРНОЙ СТРУКТУРЕ ПОЛИМЕРОВ
Полимерные материалы отличаются от металлов,
ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ О МОЛЕКУЛЯРНОЙ И НАДМОЛЕКУЛЯРНОЙ СТРУКТУРЕ ПОЛИМЕРОВ
Полимерные материалы отличаются от металлов,

Эта и другие специфические особенности механических свойств полимеров связаны с особенностями строения длинных цепных молекул, прежде всего с их гибкостью. Исследование механизма деформации на молекулярном уровне показывает, что причиной высокоэластичности является броуновское движение*, в котором участвуют отдельные подвижные элементы (сегменты) гибкой молекулы.
Под воздействием броуновского движения молекула принимает статистически беспорядочные конформации; при этом расстояние между ее концами стремится к минимуму. При деформации полимера, например при растяжении, молекулы принимают менее вероятные конформации, расстояние между их концами увеличивается, и появляется сила, стремящаяся при снятии внешней нагрузки изменить конформации макромолекул на более вероятные.
_____________________________________
* Роберт Браун (Robert Brown 1773 — 1858) — британский ботаник конца XVIII — первой половины XIX века, морфолог и систематик растений, первооткрыватель «броуновского движения»)
Слайд 12Для наглядного подтверждения основных положений была создана физическая
модель линейной макромолекулы, увеличенной
Для наглядного подтверждения основных положений была создана физическая
модель линейной макромолекулы, увеличенной

При таком увеличении диаметр модели составлял около 1 см, а сама макро-молекула имела вид нити с нанизанными на нее бусинками, каждая из которых отвечает трем углеродным атомам цепи. Нить, на которую нанизано 330 бусинок, моделирует молекулу, состоящую из 103 углеродных атомов, что соответствует молекулярной массе, примерно равной 14000.
Трехмерная модель единичной
макромолекулы
и взаимное переплетение
перекрытие двух
макромолекул, помещенной в
поле случайных сил.
Если в воду поместить одновременно 10—20 коротких цепей, то эти «молекулы» распределяются по всему объему равномерно. Однако если короткие цепи соединить вместе, то бусинки не могут перемещаться независимо друг от друга, и модель принимает форму, показанную рисунке. Если нить полностью вытянуть и затем отпустить, то непрерывно колеблющиеся бусинки сразу заставляют ее скручиваться и изгибаться так, что ее концы сближаются. Эти же эксперименты подтвердили, что расстояние между концами макромолекулы изменяется обратно пропорционально корню квадратному из числа узлов, как это и предсказывает-ся теорией. Если в аквариум поместить несколько нитей, то они взаимно проникают друг в друга и переплетаются. Если к такому «раствору» приложить напряжение сдвига, то образуют типичные длинноцепочные зацепления.
Слайд 13Отсутствие в представленной модели сил межмолекулярного взаимодействия ограничивает применимость такой модели областью
Отсутствие в представленной модели сил межмолекулярного взаимодействия ограничивает применимость такой модели областью

Однако очевидно, что аналогичные конформации образуются как в расплавах полимеров, так и в полимерах, находящихся в высокоэластичном (каучукоподобном) состоянии.
В конденсированном состоянии существенные осложнения вносит наличие сил межмолекулярного взаимодействия различного типа (ван-дер-ваальсовы* силы, взаимодействие между полярными группами, водородные связи и т. д.).
Переходы от одной конформации к другой не могут осуществляться совершенно свободно, так как вращение отдельных групп относительно ординарных связей заторможено.
Важнейшую роль в процессе деформации играет гибкость макромолекулы. Характер связей вдоль линейной молекулы и между отдельными группами соседних цепей различен. В первом случае речь идет о прочных химических связях, а во втором — об относительно слабых связях за счёт межмолекулярного взаимодействия. Однако суммарное усилие, образованное большим числом слабых связей, приложенных к отдельной молекуле, может оказаться соизмеримо с прочностью химической связи.
Многочисленные экспериментальные исследования структуры полимеров в конденсированном состоянии показали, что основной структурной единицей полимерных тел является пучок макромолекул.
___________________________________
* Йоханнес Дидерик ван дер Ваальс (Johannes Diderik van der Waals, 1837 — 1923) —голландский физик лауреат Нобелевской премии по физике в 1910 году. В первую очередь известен открытием уравнения с хорошей точностью описывающее поведение реального газа.
Слайд 14 Длинные и гибкие макромолекулы, способные как к свернутым, так и к
Длинные и гибкие макромолекулы, способные как к свернутым, так и к

Ламели, в свою очередь, могут образовывать и более сложные структуры: фибриллы, ленты, сферолиты и даже крупные единичные кристаллы.
В случае аморфных полимеров пучки укладываются в крупные надмолекулярные образования — домены, внутри которых могут существовать области с высокой степенью упорядоченности. В соответствии с классификацией, предложенной
В. А. Каргиным* различают следующие структуры:
а) глобулярные структуры. Глобулы состоят из одной или нескольких полимерных молекул, скрученных в образования сферической формы;
б) полосатые структуры, образованные пучками молекул, располагающимися по зигзагообразно сходящимся линиям и не имеющими четко различимых границ раздела; структуры такого типа характерны для эластомеров;
в) пачечно-фибриллярные структуры, образованные пучками, в каждый из которых входит по нескольку десятков или сотен выпрямленных макромолекул; такие структуры обычно присутствуют в хорошо упорядоченных аморфных полимерах, находящихся в стеклообразном состоянии, или в кристаллизующихся полимерах на разных стадиях кристаллизации;
____________________________________________
* Валентин Алексеевич Каргин (1907—1969) — советский физикохимик , специалист по коллоидной химии и полимерам, основатель советской полимерной школы
Слайд 15г) сферолиты — крупные структурные образования, построенные из пачек и фибрилл; эти
г) сферолиты — крупные структурные образования, построенные из пачек и фибрилл; эти

д) сложные структуры типа лент, образованных агрегированными между собой сферолитами;
ё) ориентированные фибриллярные структуры, состоящие из центрального стержня, на который нанизаны изогнутые пластины или диски.
Аморфные полимеры
Основной морфологической единицей аморфного полимера является пачка (фибрилла), состоящая из доменов со складчатыми цепями; участки цепей между складками уложены в основном параллельно друг другу, но дальний порядок, характерный для кристалтлических полимеров, отсутствует.
Домены — это небольшие, относительно плотно упакованные участки фибриллы размером 30—100 Å *. Каждая цепь может принадлежать одновременно нескольким доменам. Число таких проходных цепей в междоменных областях значительно меньше, чем число цепей, образующих складки домена. Участки проходных цепей, находящиеся между доменами, могут иметь различную длину и различные конформации. В ряде случаев в междоменных областях могут располагаться и отдельные макромолекулы.
___________________________________
* Ангстрем (русское обозначение Å) — устаревшая внесистемная единица измерения длины, равная 10−10 м
(1 Å = 0,1 нм = 100 пм; 10 000 Å = 1 мкм). Названа в честь шведского физика и астронома Андерса Ангстрема, предложившего её в 1868 году.
Ранее данная единица измерения часто использовалась в физике, поскольку 10−10 м— это приблизительный диаметр орбиты электрона во невозбуждённом атоме водорода. Тот же порядок имеет шаг атомной решётки в большинстве кристаллов. В русском языке произносится ангстрэм , по-шведски — онгстрём.
Слайд 16Кристаллические полимеры
Наиболее часто при медленной кристаллизации возникают фибриллярные кристаллы, которые имеют форму
Кристаллические полимеры
Наиболее часто при медленной кристаллизации возникают фибриллярные кристаллы, которые имеют форму
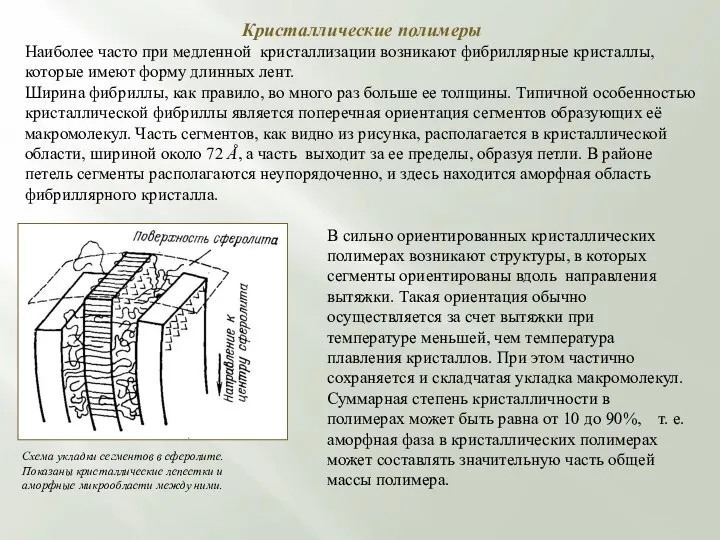
Ширина фибриллы, как правило, во много раз больше ее толщины. Типичной особенностью кристаллической фибриллы является поперечная ориентация сегментов образующих её макромолекул. Часть сегментов, как видно из рисунка, располагается в кристаллической области, шириной около 72 Å, а часть выходит за ее пределы, образуя петли. В районе петель сегменты располагаются неупорядоченно, и здесь находится аморфная область фибриллярного кристалла.
Схема укладки сегментов в сферолите.
Показаны кристаллические лепестки и
аморфные микрообласти между ними.
В сильно ориентированных кристаллических полимерах возникают структуры, в которых сегменты ориентированы вдоль направления вытяжки. Такая ориентация обычно осуществляется за счет вытяжки при температуре меньшей, чем температура плавления кристаллов. При этом частично сохраняется и складчатая укладка макромолекул. Суммарная степень кристалличности в полимерах может быть равна от 10 до 90%, т. е. аморфная фаза в кристаллических полимерах может составлять значительную часть общей массы полимера.
Слайд 17
Переход от кристаллической к аморфной фазе в полимерах осуществляется постепенно, через
Переход от кристаллической к аморфной фазе в полимерах осуществляется постепенно, через

Эти формы могут быть сравнительно высокоупорядоченными, например кристаллиты, или практически совершенно лишенными признаков дальнего порядка, подобно аморфным областям.
Методы определения количественного содержания кристаллической фазы, такие, как:
рентгеноструктурный метод,
дилатометрия и др., дают разные значения степени кристалличности вследствие специфики самих структур и разной чувствительности методов.
Это следует иметь в виду, сопоставляя значения степени кристалличности, которые приводятся в литературе.
Слайд 18ДЕФОРМАЦИОННЫЕ СВОЙСТВА ПОЛИМЕРОВ
В ЗАВИСИМОСТИ ОТ ТЕМПЕРАТУРЫ
Температура оказывает сильное влияние на
ДЕФОРМАЦИОННЫЕ СВОЙСТВА ПОЛИМЕРОВ
В ЗАВИСИМОСТИ ОТ ТЕМПЕРАТУРЫ
Температура оказывает сильное влияние на

Опыт показывает, что в области низких температур, при которых возмущающее действие теплового движения невелико, полимер ведет себя аналогично простому твердому низкомолекулярному веществу. При повышении температуры интенсивность теплового движения возрастает, и при некотором ее значении, когда энергия теплового движения сегмента оказывается соизмеримой с энергетическими барьерами, обусловленными силами межмолекулярного взаимодействия, полимер приобретает способность к высокоэластической деформации.
Однако наличие значительного числа переплетений или мелких кристаллических областей, играющих роль поперечных связей, препятствует его превращению в жидкость.
При дальнейшем повышении температуры энергия теплового движения сегментов возрастает настолько, что оказывается соизмеримой с уровнем наиболее значительных энергетических барьеров. Тепловое движение разрушает даже наиболее сильно упорядоченные кристаллические области. Зацепления и точки взаимодействия приобретают явно флуктуационный характер, возникая и разрушаясь под действием теплового движения. В этом случае полимер находится, как принято говорить, в жидкотекучем состоянии.
Таким образом, полимеры могут существовать в двух агрегатных состояниях: твёрдом и жидком.
Слайд 19Фазовые состояния полимера
В термодинамике различают:
- кристаллические,
- жидкие
- газовые
Фазовые состояния полимера
В термодинамике различают:
- кристаллические,
- жидкие
- газовые

Переход из одной кристаллической формы в другую сопровождается переменой характера (перестроением) кристаллической упаковки и является следствием изменения дальнего порядка.
Переход в жидкое состояние происходит при полном разрушении дальнего порядка. Поэтому, в отличие от кристаллических тел, тела, находящиеся в жидком состоянии, называют стеклами, а фазовое состояние — стеклообразным.
В отличие от низкомолекулярных веществ аморфные полимеры обладают еще одним физическим состоянием — высокоэластическим.
Полимер в высокоэластическом состоянии способен к значительной обратимой деформации, и поэтому его нельзя рассматривать как обычное стеклообразное тело. С другой стороны, в этом состоянии полимер неспособен к большим необратимым деформациям и, следовательно, не является жидкостью.
Слайд 20Некоторые термины, понятия и определения
ТЕМПЕРАТУРА ТЕКУЧЕСТИ (fluidity temperaturе Tf ) - температура,
Некоторые термины, понятия и определения
ТЕМПЕРАТУРА ТЕКУЧЕСТИ (fluidity temperaturе Tf ) - температура,

Для кристаллизующихся полимеров температура текучести практически совпадает с температурой плавления, для аморфных полимеров - соответствует переходу из высокоэластического состояния в вязкотекучее. Для некоторых полимеров с относительно малой молекулярной массой возможен переход непосредственно из стеклообразного состояния; тогда температура текучести совпадает с температурой рой стеклования.
Температура плавления и отвердевания (melting point temperature Тм температура, при которой твёрдое кристаллическое тело совершает переход в жидкоесостояние и наоборот. При температуре плавления вещество может находиться как в жидком, так и твёрдом состоянии. При подведении дополнительного тепла вещество перейдёт в жидкое состояние,
а температура не будет меняться, пока всё вещество в рассматриваемой системе нерасплавится. При отведении лишнего тепла (охлаждении) вещество будет переходить в твёрдое состояние (застывать) и, пока оно не застынет полностью, температура не изменится.
Смеси веществ не имеют температуры плавления/отвердевания и совершают переход в некотором диапазоне температур (температура появления жидкой фазы называется точкой солидуса, температура полного плавления точкой ликвидуса). Но некоторые смеси (эвтектическогосостава) обладают определенной температурой плавления, как чистые вещества.
Слайд 21 Аморфные вещества, как правило, не обладают чёткой температурой плавления ростом температуры снижается вязкость таких веществ, и чем ниже вязкость, тем более жидким становится материал.
Поскольку при плавлении объём тела меняется незначительно, давление мало влияет на температуру плавления.
Температура стеклования полимеров (glass transition temperature Tg) – это температура, при которой полимер при
Аморфные вещества, как правило, не обладают чёткой температурой плавления ростом температуры снижается вязкость таких веществ, и чем ниже вязкость, тем более жидким становится материал.
Поскольку при плавлении объём тела меняется незначительно, давление мало влияет на температуру плавления.
Температура стеклования полимеров (glass transition temperature Tg) – это температура, при которой полимер при

Поскольку этот переход осуществляется в интервале температур, достигающих нескольких десятков градусов, температура стеклования характеризует его условно и зависит от скорости охлаждения и способа определения.
Температура стеклования определяется химическим составом и строением цепи полимера. Наиболее низкие значения температуры стеклования характерны для неполярных полимеров с гибкими макромолекулами, наиболее высокие – для полярных с жесткими. Точные значения температуры стеклования для высоко-кристаллических полимеров пока не известны из-за невозможности разделить в образце аморфную и кристаллическую части.
Температура стеклования – это важная эксплуатационная характеристика полимерного материала, так как она соответствует верхней температурной границе теплостойкости пластмасс и нижней границе морозостойкости каучуков и резин.
Температура стеклования существенно зависит от частоты и интенсивности воздействия на полимер. Поэтому различные методы определения температуры стеклования могут давать несовпадающие значения.
Слайд 22ТЕРМОМЕХАНИЧЕСКИЕ КРИВЫЕ –
КАК МЕТОД ЭКСПЕРИМЕНТАЛЬНОГО
ИССЛЕДОВАНИЯ ФАЗОВОГО СОСТОЯНИЯ
Один из наиболее простых методов
ТЕРМОМЕХАНИЧЕСКИЕ КРИВЫЕ –
КАК МЕТОД ЭКСПЕРИМЕНТАЛЬНОГО
ИССЛЕДОВАНИЯ ФАЗОВОГО СОСТОЯНИЯ
Один из наиболее простых методов

Сущность этого метода состоит в том, что определяется температурная зависимость деформации, развивающейся в испытуемом образце под постоянной нагрузкой, прикладываемой к образцу на одно и то же время, например, равное 10 секундам. Оценивается измерение величины деформации образца полимера ε под действием силы F в условиях непрерывного нагрева.
Результаты таких измерений представляют в виде графика деформация — температура ε = f(Т) , известного под названием термомеханической кривой.
Слайд 23Типичная термомеханическая кривая аморфного полимера - на рисунке.
По этой кривой можно
Типичная термомеханическая кривая аморфного полимера - на рисунке.
По этой кривой можно

Аморфные полимеры
Термомеханическая кривая линейного аморфного полимера
Температура текучести определяет нижняя границу температурного интервала переработки полимера. Так, невысокие значения температуры текучести (150-250°С) большинства пластмасс благоприятствуют их переработке в изделия.
Длятермостойких полимеров характерны относительно высокие температуры текучести (> 250 °С), близкие к температуре разложения, что затрудняет формование изделий из них.
Слайд 24Температурные переходы.
Способы графического определения температур фазовых переходов.
Ширина области температурного перехода может составлять
Температурные переходы.
Способы графического определения температур фазовых переходов.
Ширина области температурного перехода может составлять
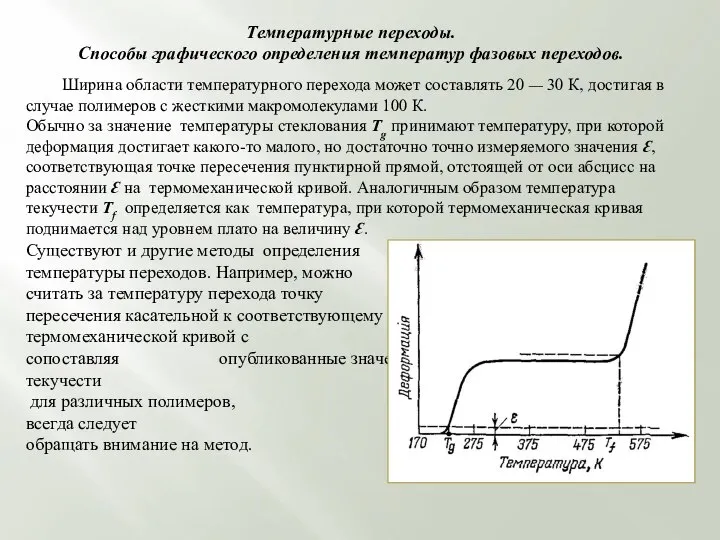
Обычно за значение температуры стеклования Tg принимают температуру, при которой деформация достигает какого-то малого, но достаточно точно измеряемого значения Ɛ, соответствующая точке пересечения пунктирной прямой, отстоящей от оси абсцисс на расстоянии Ɛ на термомеханической кривой. Аналогичным образом температура текучести Tf определяется как температура, при которой термомеханическая кривая поднимается над уровнем плато на величину Ɛ.
Существуют и другие методы определения
температуры переходов. Например, можно
считать за температуру перехода точку
пересечения касательной к соответствующему участку термомеханической кривой с осью абсцисс. Поэтому, сопоставляя опубликованные значения температур стеклования и текучести
для различных полимеров,
всегда следует
обращать внимание на метод.
Слайд 25Кристаллические полимеры
Типичные термомеханические кривые для кристаллических полимеров представлены на рисунке.
Ряд кристаллических полимеров
Кристаллические полимеры
Типичные термомеханические кривые для кристаллических полимеров представлены на рисунке.
Ряд кристаллических полимеров
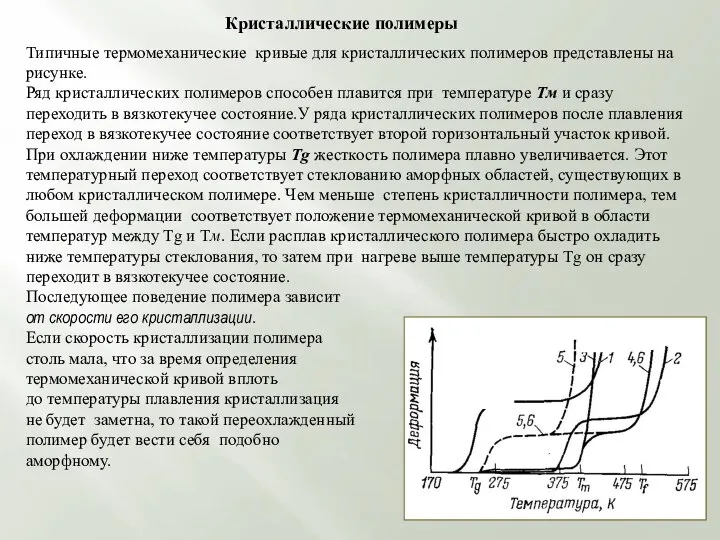
При охлаждении ниже температуры Tg жесткость полимера плавно увеличивается. Этот температурный переход соответствует стеклованию аморфных областей, существующих в любом кристаллическом полимере. Чем меньше степень кристалличности полимера, тем большей деформации соответствует положение термомеханической кривой в области температур между Tg и Тм. Если расплав кристаллического полимера быстро охладить ниже температуры стеклования, то затем при нагреве выше температуры Tg он сразу переходит в вязкотекучее состояние.
Последующее поведение полимера зависит
от скорости его кристаллизации.
Если скорость кристаллизации полимера
столь мала, что за время определения
термомеханической кривой вплоть
до температуры плавления кристаллизация
не будет заметна, то такой переохлажденный
полимер будет вести себя подобно
аморфному.
Слайд 26I участок - стеклообразное состояние; в тепловом движении участвуют атомы или группы
I участок - стеклообразное состояние; в тепловом движении участвуют атомы или группы

Переходный участок – появляется подвижность сегментов, полимер “расстекловывает-ся”; величина деформации ε возрастает с ростом температуры; полимер уже не ведет себя как твёрдое, жёсткое тело, но и не является пока истинным эластомером.
II участок – высокоэластическое состояние; в тепловом движении участвуют атомы и группы атомов, колеблющиеся относительно положения равновесия, сегменты, которые перемещаются в
Термомеханическая кривая
поле действия механических сил, что соп-
ровождается изменением формы макро-молекул. ВЭД обратима; величина дос-тигает нескольких сотен процентов, прак-тически не зависит от температуры.
III участок - вязко текучее состояние, когда движение сегментов в поле действия механических сил приводит к смещению центра тяжести макромолекул, помещению макромолекул относительно друг друга – необратимая деформация течения, величина которой увеличивается с ростом температуры. Если при снятии ТМК не происходит деструкция, то при медленном охлаждении образец последовательно переходит из ВТС в ВЭС и СТС.
Слайд 27 Структурное стеклование.Под действием теплового движения, узлы сетки распадаются в одном месте
Структурное стеклование.Под действием теплового движения, узлы сетки распадаются в одном месте

Механическое стеклование.Характерно для полимеров, находящихся в ВЭС; заключается в потере способности полимера к ВЭД при увеличении скорости деформации. Когда скорость действия силы велика, превышает скорость внутренних перестроек в образце, в нем не успевает развиваться ВЭД → полимер ведет себя как застеклованный, твердый полимер.
Механическое стеклование отличается от структурного тем, что тепловое движение не прекращается, структура - не фиксируется.
Температура структурного стеклования, определяемая в отсутствие механических воздействий, не является строго фиксированной величиной это некоторый интервал, зависящий от скорости охлаждения и способа определения.
Температуры структурного стеклования и механического стеклования не совпадают между собой, так как первая зависит от скорости охлаждения,
а вторая — от режима механического воздействия.
Слайд 28Факторы, влияющие на температуру структурного стеклования:
- скорость охлаждения;
- гибкость
Факторы, влияющие на температуру структурного стеклования:
- скорость охлаждения;
- гибкость

- молекулярная масса полимера.
Скорость охлаждения. При медленном охлаждении сегменты успевают перемещаться даже при температурах близких к Тсс, поэтому требуется сильнее охладить полимер, для прекращения любой перестройки. Т.о. чем выше скорость охлаждения, тем выше измеренная Тсс.
Температура стеклования - это средняя температура некоторой области, поскольку переход в стеклообразное состояние обычно происходит в определенном температурном интервале.
Гибкость цепи полимера. Неполярные полимеры с высокой гибкостью характеризуются низкими значениями Тсс. Наличие полярных групп увеличивает межмолекулярное взаимодействие и повышает Тсс. На Тсс оказывает влияние расположение полярных групп. Наличие объёмных заместителей ведет к росту Тсс ,
например, в сополимерах стирола и бутадиена в ряду:
СКС-10 -80 °С , СКС-30 -72 °С , СКС-60 -24 °С.
Молекулярная масса полимера влияет на Тсс : при переходе от олигомера к полимеру Тсс возрастает, достигая постоянного значения; с дальнейшим ростом молекулярной массы полимера практически не изменяется.
Слайд 29ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУР ФАЗОВЫХ ПЕРЕХОДОВ ПОЛИМЕРОВ
МЕТОДАМИ ТЕРМИЧЕСКОГО АНАЛИЗА
Дифференциальный термический анализ (ДТА) — метод
ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУР ФАЗОВЫХ ПЕРЕХОДОВ ПОЛИМЕРОВ
МЕТОДАМИ ТЕРМИЧЕСКОГО АНАЛИЗА
Дифференциальный термический анализ (ДТА) — метод

Сущность метода заключается в фиксации тепловых эффектов, возникающих в исследуемом веществе при структурных или химических превращениях в нем и наблюдающихся в процессе нагрева или охлаждения образца. Как правило, внутренние процессы сопровождаются выделением (экзотермические ↑) или поглощением (эндотермические ↓) тепловой энергии. ДТА является наиболее распространенным
методом термического анализа из-за широкого спектра получаемой информации.
В качестве эталонного образца используется инертное в вещество с близкими к
Исследуемому веществу значениями тепло-
ёмкости и теплопроводности, которое
в исследуемом диапазоне температур
не испытывает никаких структурных
и фазовых изменений. Таким образом
возникающая при одновременном
нагреве или охлаждении исследуемого
и эталонного образцов разность
температур между ними обусловливается
эндо- или экзотермическими превраще-
ниями или реакциями в исследуемом образце.
Слайд 31 Дифференциальная сканирующая калориметрия (ДСК) –
Термоаналитическая методика, в которой разница в количестве тепла, необходимого для
Дифференциальная сканирующая калориметрия (ДСК) –
Термоаналитическая методика, в которой разница в количестве тепла, необходимого для

И образец, и эталон поддерживаются при практически одинаковой температуре в тече-ние всего эксперимента.
Температурная программа для анализа ДСК разработана таким образом, что температу-ра держателя образца линейно увеличивается как функция времени. Контрольный образец должен иметь хорошо определенную теплоёмкость в диапазоне температур, подлежащих сканированию.
ДСК широко используется при исследовании полимерных материалов для определения их тепловых переходов.
Наблюдаемые тепловые переходы можно использовать для сравнения материалов, хотя одни только переходы однозначно не определяют состав.
Исследование химического и фазового состава неизвестных материалов может быть завершено с использованием дополнительных инструментальных методов физико-химического анализа веществ. Точки плавления и стеклования для большинства полимеров доступны в стандартных справочниках, и ДСК исследование может показать деградацию полимера при снижении ожидаемой температуры плавления.
Tm зависит от молекулярной массы полимера и его термической предыстории.
Процент кристаллического содержания полимера может быть оценен по пикам кристаллизации / плавления кривой ДСК.
Слайд 32ОСНОВНЫЕ ВИДЫ ДЕФОРМАЦИИ
Почти все полимерные материалы в определенном температурном интервале способны к
ОСНОВНЫЕ ВИДЫ ДЕФОРМАЦИИ
Почти все полимерные материалы в определенном температурном интервале способны к

Для линейных аморфных полимеров этот температурный интервал, по существу, представляет собой всю область температур, лежащую выше температуры стеклования. Для кристаллических полимеров — это область температур, расположенная выше температуры плавления кристаллических областей.
Разумеется, в обоих случаях сверху эта область ограничивается температурой разложения для термопластичных материалов и температурой структурирования для термореактивных материалов.
Всякую конечную деформацию реального материала можно представить как результат последовательного проявления двух принципиально отличных видов деформации: деформации объёмного сжатия или расширения, характеризующейся изменением объёма при неизменной форме; деформации сдвига, характеризующейся изменением формы при неизменном объеме.
Взаимное соотношение этих двух видов деформации в процессах деформации реальных материалов определяется физической константой материала, называемой коэффициентом Пуассона*.
______________________________________
Симеон Дени Пуассон (фр. Siméon Denis Poisson; 1781- 1840) - французский математик, механик
и физик.
Слайд 33Рассмотрим призму длиной l0, к торцу которой приложено растягивающее напряжение σ0. Предположим,
Рассмотрим призму длиной l0, к торцу которой приложено растягивающее напряжение σ0. Предположим,

Относительное изменение объёма при этом равно: Δv/v0 = (1-2 μ) σ0/Е,
где Δv/v0 — изменение объема образца; v0 — первоначальный объем образца
Для всех полимерных систем при температурах выше температуры стеклования или плавления значение коэффициента Пуассона близко к 0,5.
Поэтому во всех случаях деформации полимерных тел эта деформация может быть сведена к изменению формы, т. е. к деформации сдвига.
___________________________________________
* Томас Юнг (англ. Thomas Young 1773— 1829 ) — английский учёный: физик, механик, врач, астроном, филолог и востоковед
Слайд 34Упругая и пластическая деформация
Рассмотрим деформацию элементарной призмы, к верхней и нижней поверхностям
Упругая и пластическая деформация
Рассмотрим деформацию элементарной призмы, к верхней и нижней поверхностям

Для призмы из абсолютно упругого материала справедливо следующее соотношение:
Величина ΔS /Н служит мерой деформации сдвига и равна tgα, а при малых значе-ниях угла α —самому углу.
В дальнейшем деформация сдвига будет обозначаться буквой γ.
Величина F/A — это тангенциальное напряжение, или напряжение сдвига, которое обозначается в дальнейшем буквой ρ. G — это мера упругости тела так называемый модуль упругости при сдвиге, или модуль сдвига. Таким образом, уравнение можно записать в следующем виде: γ = ρ /G . Это уравнение известно как закон Гука*.
Графически закон Гука можно изобразить в виде прямой, иллюстрирующей прямую пропорциональность между напряжением и деформацией – кривая 1
_____________________________
* Роберт Гук (англ. Robert Hooke; 1635 — 1703) — английский естествоиспытатель и изобретатель.
Слайд 35ДИАГРАММА НАПРЯЖЕНИЕ — ДЕФОРМАЦИЯ
Термомеханическая кривая описывает механические свойства полимеров при малых деформациях.
ДИАГРАММА НАПРЯЖЕНИЕ — ДЕФОРМАЦИЯ
Термомеханическая кривая описывает механические свойства полимеров при малых деформациях.

Как правило, механические свойства определяют на образцах, имеющих форму двухсторонних лопаток.
Такая форма выбирается для того, чтобы свести к минимуму неоднородность поля напряжений в рабочем участке образца. За рабочий участок принимают прямолинейную часть образца, имеющую постоянное поперечное сечение. Условное напряжение чаще всего определяют делением действующей силы на площадь первоначального сечения образца. Более правильно было бы определять истинные напряжения, относя действующую силу к фактической площади поперечного сечения, так как при больших удлинениях, наблюдающихся при испытаниях полимеров, начальная площадь сечения уменьшается в несколько раз.
Слайд 36Семейство типичных диаграмм растяжения аморфного полимера в координатах условное напряжение — деформация,
Семейство типичных диаграмм растяжения аморфного полимера в координатах условное напряжение — деформация,
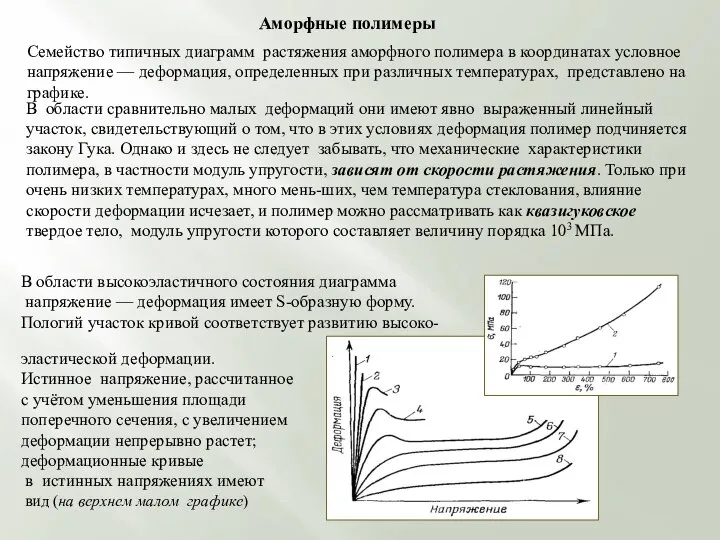
Аморфные полимеры
В области сравнительно малых деформаций они имеют явно выраженный линейный участок, свидетельствующий о том, что в этих условиях деформация полимер подчиняется закону Гука. Однако и здесь не следует забывать, что механические характеристики полимера, в частности модуль упругости, зависят от скорости растяжения. Только при очень низких температурах, много мень-ших, чем температура стеклования, влияние скорости деформации исчезает, и полимер можно рассматривать как квазигуковское твердое тело, модуль упругости которого составляет величину порядка 103 МПа.
В области высокоэластичного состояния диаграмма
напряжение — деформация имеет S-образную форму.
Пологий участок кривой соответствует развитию высоко-
эластической деформации.
Истинное напряжение, рассчитанное
с учётом уменьшения площади
поперечного сечения, с увеличением
деформации непрерывно растет;
деформационные кривые
в истинных напряжениях имеют
вид (на верхнем малом графике)
Слайд 37Вынужденная высокоэластическая деформация
Молекулярный механизм развития вынужденно-эластической деформации в основном идентичен механизму обычной
Вынужденная высокоэластическая деформация
Молекулярный механизм развития вынужденно-эластической деформации в основном идентичен механизму обычной

Отличие состоит в том, что энергии теплового движения при температурах ниже температуры стеклования оказывается недостаточно для преодоления сил межмолекулярного взаимодействия. Приложение внешнего механического поля снижает потенциальные барьеры, и полимерные молекулы могут проявить гибкость, обеспечивающую развитие высоко-эластических деформаций. Поэтому, когда действующие напряжения достигают критического значения, соответствующего уровню, необходимому для растормаживания теплового движения, застеклованное полимерное тело вновь переходит в каучукоподобное состояние.
Развитие вынужденно-эластической деформации начинается в самом слабом сечении образца и сопровождается образованием «шейки» — местного резкого уменьшения сечения образца, которое постепенно распространяется в обе стороны вдоль образца по направлению к зажимам. В момент возникновения шейки на деформационной кривой появляется максимум. Образование максимума связано с резким уменьшением истинного сечения, появлением микротрещин и даже разогревом материала в районе шейки.
Напряжение, соответствующее точке максимума, обычно называют пределом текучести, хотя по своему физическому смыслу — это скорее предел вынужденной эластичности. Пологий участок кривой, в пределах которого напряжение растет очень незначительно, соответствует этапу постепенного распространения шейки на всю длину образца. Когда весь материал переходит в шейку, образец вновь начинает деформироваться как единое целое, и напряжение начинает быстро увеличиваться. Как только степень вытяжки окажется достаточной для увеличения предела вынужденной эластичности, развитие вынужденной эластической деформации в этой части образца прекратится.
Слайд 38Кристаллические полимеры
Диаграммы растяжения кристаллических полимеров очень похожи на диаграммы растяжения аморфных
Кристаллические полимеры
Диаграммы растяжения кристаллических полимеров очень похожи на диаграммы растяжения аморфных

При более высоких температурах кристаллические поли-
меры проявляют способность к вынужденно-эластическо
деформации (кривые 3—7).
Молекулярный механизм развития вынужденной
эластической деформации кристаллических полимеров
принципиально отличается от рассмотренного выше. Подвижность полимерных молекул ограничивается наличием кристаллических областей. Следовательно, любое изменение конформации полимерной цепи влечет за собой изменение кристаллической структуры
Действие механических напряжений по-разному изменяет температуру плавления различных элементов структуры. Для благоприятно ориентированных элементов температура плавления повышается и, следовательно, возрастает их стабильность. Напротив, температура плавления элементов с неблагоприятной ориентацией может существенно снизиться; поэтому в процессе деформации эти структурные элементы плавятся и потом вновь кристаллизуются в виде более устойчивых структурных форм.
Слайд 39РЕЛАКСАЦИОННЫЕ ЯВЛЕНИЯ ПРИ ДЕФОРМАЦИИ ПОЛИМЕРОВ
Процесс деформации — это процесс изменения конформации макромолекул
РЕЛАКСАЦИОННЫЕ ЯВЛЕНИЯ ПРИ ДЕФОРМАЦИИ ПОЛИМЕРОВ
Процесс деформации — это процесс изменения конформации макромолекул

Все явления, обусловленные переходом от неравновесных состояний к равновесным под действием теплового движения, называются релаксационными.
Сам переход от одного состояния к другому совершается не мгновенно, а требует для своего протекания определённого промежутка времени, тем большего, чем:
меньше интенсивность теплового движения (т. е. чем ниже температура),
больше масса перемещаемых элементов структуры (т. е. чем выше молекулярная масса сегмента)
больше силы межмолекулярного взаимодействия.
Если в качестве меры отклонения от равновесия ввести величину у, то при малых отклонениях от равновесия скорость приближения системы к равновесному значению dy/dt будет прямо пропорциональна отклонению: dy/dt = - уτ .
Интегрируя уравнение и определяя постоянную интегрирования из условия у = у0 при t = 0, получим: у = у0 • е -t/τ
Характеристика релаксационного процесса τ называется временем релаксации. Физический смысл времени релаксации состоит в следующем: это время, в течение которого начальное значение параметра у уменьшается в е раз.
При исследовании релаксационных явлений большое значение имеет соотношение между временем релаксации и продолжительностью опыта.
Слайд 40Динамический механический анализ (ДМА)
Применяется для исследований зависимости механических и вязкоупругих свойств материалов
Динамический механический анализ (ДМА)
Применяется для исследований зависимости механических и вязкоупругих свойств материалов

Слайд 41Теория
Инструменты ДМА прилагают колебательную силу (напряжение) и регистрируют осциллирующее изменение образца.
Модуль
Теория
Инструменты ДМА прилагают колебательную силу (напряжение) и регистрируют осциллирующее изменение образца.
Модуль

Оборудование
Образец размещается между двумя захватами или ограничителями.
Затем к образцу прилагается колебательное (динамическое) усилие.
Его вызывают с помощью электродвигателя с вращательными движениями (обычно взад-вперед) и линейными движениями (обычно вверх-вниз), который также характеризуется частотой (скорость колебаний) и усилием (энергия, прилагаемая к образцу).
Получаемая в результате деформация (перемещение) обычно измеряется с помощью преобразователя линейного перемещения в цифровой сигнал, или датчика силы. Обычно строится график зависимости динамического модуля упругости и тангенса механических потерь.
Слайд 43ОСОБЕННОСТИ ТЕЧЕНИЯ ПОЛИМЕРОВ
У большинства жидкостей коэффициент вязкости η зависит только от при-роды
ОСОБЕННОСТИ ТЕЧЕНИЯ ПОЛИМЕРОВ
У большинства жидкостей коэффициент вязкости η зависит только от при-роды

У некоторых жидкостей, преимущественно высокомолекулярных или представля-ющих дисперсионные системы (суспензии и эмульсии), η зависит также от режима течения - давления и градиента скорости. При их увеличении вязкость жидкости уменьшается вследствие нарушения внутренней структуры потока жидкости. Их вязкость характеризуют так называемым условным коэффициентом вязкости, который относится к определенным условиям течения жидкости (давление, скорость). Такие жидкости называются структурно вязкими или неньютоновскими.
Вязкое течение. Рассмотрим деформацию призмы, вырезанной в жидкости.
Если деформация осуществляется бесконечно медленно, то возникающие при этом напряжения бесконечно малы, т. е. слои жидкости сдвигаются относительно друг друга практически без всякого сопротивления.
Однако как только скорость смещения слоев становится конечной, сразу же возникает сопротивление сдвигу. Для вязких ньютоновских жидкостей сила сопротивления тем больше, чем больше скорость деформации dy/dt.
Математически закон Ньютона запишется так: dγ/dt = ρ /η , где dγ/dt - скорость сдвига; η - коэффициент вязкости.
В случае одномерного течения вместо скорости деформации dγ/dt можно воспользова-ться градиентом скорости U/H (где U — скорость смещения верхнего основания призмы оносительно нижнего). Для двумерного и трехмерного течения такая замена неправомерна.
Слайд 44Графически можно изобразить закон Ньютона прямой с угловым коэффициентом, равным 1/η (прямая
Графически можно изобразить закон Ньютона прямой с угловым коэффициентом, равным 1/η (прямая
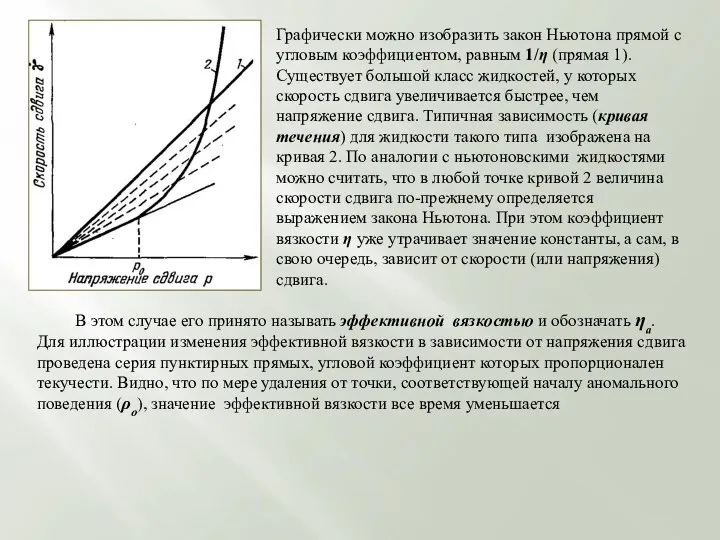
Существует большой класс жидкостей, у которых скорость сдвига увеличивается быстрее, чем напряжение сдвига. Типичная зависимость (кривая течения) для жидкости такого типа изображена на кривая 2. По аналогии с ньютоновскими жидкостями можно считать, что в любой точке кривой 2 величина скорости сдвига по-прежнему определяется выражением закона Ньютона. При этом коэффициент вязкости η уже утрачивает значение константы, а сам, в свою очередь, зависит от скорости (или напряжения) сдвига.
В этом случае его принято называть эффективной вязкостью и обозначать ηа.
Для иллюстрации изменения эффективной вязкости в зависимости от напряжения сдвига проведена серия пунктирных прямых, угловой коэффициент которых пропорционален текучести. Видно, что по мере удаления от точки, соответствующей началу аномального поведения (ρо), значение эффективной вязкости все время уменьшается
Слайд 45Тело Максвелла.
Представления об упругости материала, полностью подчиняющегося закону Гука, и вязкой
Тело Максвелла.
Представления об упругости материала, полностью подчиняющегося закону Гука, и вязкой

Рассмотрим простейшие механические модели, обладающие в отдельности свойствами упругого тела и ньютоновской жидкости.
В качестве простейшей модели упругого тела воспользуемся обычной пружиной. Единственной характеристикой такой пружины является ее жесткость, которую будем считать равной модулю сдвига G. В том случае, если к этой пружине приложено усилие, вызывающее напряжение ρ, её деформация будет описываться уравнением γ = ρ /G .
В качестве простейшей механической модели ньютоновской жидкости восполь-зуемся цилиндрическим поршнем, передвигающимся в сосуде, заполненном вязкой ньютоновской жидкостью. Между силой, приложенной к поршню, и скорос-тью его смещения будет соблюдаться зависимость dγ/dt = ρ/η.
.
__________
* Джеймс Клерк Максвелл (англ. James Clerk Мaxwell 1831—1879 )британский (шотландский) физик, математик.
Рассмотрим простейшую комбинацию, образованную из этих двух последовательно соединенных элементов. Такое модельное тело, обладающее одновременно упругостью и вязкостью, называется телом Максвелла*
Слайд 46 Если подвергнуть тело Максвелла деформации, приложив к нему постоянное усилие, то
Если подвергнуть тело Максвелла деформации, приложив к нему постоянное усилие, то
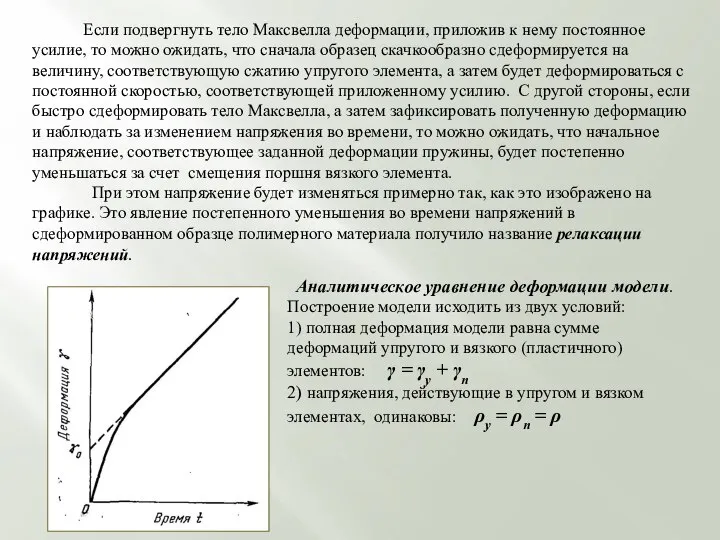
При этом напряжение будет изменяться примерно так, как это изображено на графике. Это явление постепенного уменьшения во времени напряжений в сдеформированном образце полимерного материала получило название релаксации напряжений.
Аналитическое уравнение деформации модели.
Построение модели исходить из двух условий:
1) полная деформация модели равна сумме деформаций упругого и вязкого (пластичного) элементов: γ = γу + γп
2) напряжения, действующие в упругом и вязком элементах, одинаковы: ρу = ρп = ρ
Слайд 47Аналитическое уравнение деформации модели
Дифференцирование уравнение по времени:
Величина dγy /dt (упругая часть)
Аналитическое уравнение деформации модели
Дифференцирование уравнение по времени:
Величина dγy /dt (упругая часть)

Значение dγп /dt находится непосредственно из уравнения dγ/dt = ρ/η.
Подставляя полученные результаты в уравнение получим дифференциальное уравнение, описывающее поведение тела Максвелла:
Слайд 48Классификация жидкостей
Существует следующая классификация жидкостей по зависимости вязких напряжений от скорости
Классификация жидкостей
Существует следующая классификация жидкостей по зависимости вязких напряжений от скорости

Ньютоновская жидкость — линейный закон: ρ= dγ/dt· η
Степенная (неньютоновская) жидкость — нелинейная, закон степенной: ρ= dγ/dt· ηn
• Псевдопластик n<1 , при медленных движениях вязкость велика, затем убывает.
• Дилатантная жидкость n>1 , вязкость растёт с увеличением скорости.
• Бингамовский пластик (жидкость) подобна модели сухого трения.
Наглядным примером бингамовской жидкости является краска — за счёт действия свя-зующих веществ возникает порог для напряжения сдвига, и она способна образовывать неподвижные слои на вертикальных поверхностях.
Для неньютоновских жидкостей возможно наблюдение и других эффектов, связанных с нелинейностью либо существованием порога.
Отдельным случаем неньютоновских жидкостей являются тиксотропные и реопексные жидкости, вязкость которых изменяется с течением времени.
Типичными примерами дилатантных жидкостей являются концентрированные суспензии твёрдых частиц;
псевдопластических — полимерные расплавы и растворы.
Слайд 49Опыт показывает, что большинство полимеров и их растворов в условиях переработки обладает
Опыт показывает, что большинство полимеров и их растворов в условиях переработки обладает
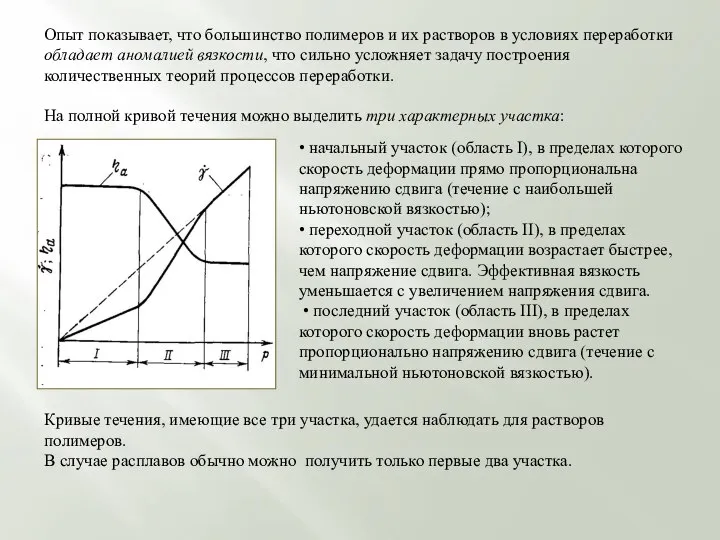
На полной кривой течения можно выделить три характерных участка:
• начальный участок (область I), в пределах которого скорость деформации прямо пропорциональна напряжению сдвига (течение с наибольшей ньютоновской вязкостью);
• переходной участок (область II), в пределах которого скорость деформации возрастает быстрее, чем напряжение сдвига. Эффективная вязкость уменьшается с увеличением напряжения сдвига.
• последний участок (область III), в пределах которого скорость деформации вновь растет пропорционально напряжению сдвига (течение с минимальной ньютоновской вязкостью).
Кривые течения, имеющие все три участка, удается наблюдать для растворов полимеров.
В случае расплавов обычно можно получить только первые два участка.
Слайд 50ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ТЕРМОДИНАМИКИ И ТЕПЛОПЕРЕДАЧИ,
ПРИМЕНЯЕМЫЕ ПРИ ОПИСАНИИ ПРОЦЕССОВ ПЕРЕРАБОТКИ ПОЛИМЕРОВ
Практически все
ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ТЕРМОДИНАМИКИ И ТЕПЛОПЕРЕДАЧИ,
ПРИМЕНЯЕМЫЕ ПРИ ОПИСАНИИ ПРОЦЕССОВ ПЕРЕРАБОТКИ ПОЛИМЕРОВ
Практически все

Поэтому при создании количественных моделей необходимо принимать во внимание суммарную энергию, которую требуется затратить для изменения, состояния полимера.
Определение полной энергии, затрачиваемой в процессе, основано на первом законе термодинамики — законе сохранения энергии
Закономерности перехода тепловой энергии при протекании процессов изучает наука о теплообмене и теплопередаче.
ТЕРМОДИНАМИЧЕСКИЕ ОСНОВЫ ПРОЦЕССОВ ПЕРЕРАБОТКИ
Закона сохранения энергии : dU = dQ-dW
Внутренняя энергия U, являющаяся термодинамической функцией состояния.
Q — это тепло, которым обмениваются система и окружающая среда;
W — работа, осуществленная над системой внешними силами или самой системой против внешних сил.
Поскольку внутренняя энергия является функцией состояния, её изменение не зависит от пути перехода системы из одного равновесного состояния в другое. Количество тепла и работа, напротив, не являются функциями состояния, поэтому их значения зависят от характера процесса.
В термодинамике используется представление об обратимом процессе, при котором система проходит через бесконечное число равновесных состояний.
Слайд 51 Механическая работа, совершаемая в обратимом процессе расширения или сжатия,
определяется уравнением:
Механическая работа, совершаемая в обратимом процессе расширения или сжатия,
определяется уравнением:

где Ρ — давление; V — удельный объём.
Давление, температуру и объём можно замерить непосредственно.
Другие параметры системы, такие, как внутренняя энергия U и энтальпия Н, можно опреде-
лить при помощи термодинамических уравнений.
Энтальпия определяется уравнением: H = U + PV . В дифференциальной форме уравнение
имеет вид: dH = dU + PdV+VdP
Используя уравнения можно получить ряд других выражений: dU = dQ-PdV и dH = dQ + VdP
Первое уравнение показывает, что если процесс протекает при постоянном объёме, то
изменение внутренней энергии равно изменению теплосодержания системы.
Очевидно, что если процесс протекает при постоянном давлении (второе уравнение), то
изменение теплосодержания системы равно изменению энтальпии.
Следовательно, теплоёмкости при постоянном давлении и постоянном объёме
определяются выражениями:
Слайд 52УРАВНЕНИЕ СОСТОЯНИЯ
Уравнение, описывающее изменение удельного объёма в зависимости от основных термодинамических
УРАВНЕНИЕ СОСТОЯНИЯ
Уравнение, описывающее изменение удельного объёма в зависимости от основных термодинамических

В настоящее время известно несколько различных форм уравнения состояния.
Уравнение Тейта*.
Обработка многочисленных экспериментальных данных по исследованию сжимаемости полимерных жидкостей показывает, что наилучшим образом эти результаты описываются эмпирическим уравнением Тейта:
1 - V/Vo(Τ) = С In [1 + Ρ/Β (Τ)]
где V — удельный объем при давлении Ρ и температуре Т;
Vo(T) —удельный объем полимера при атмосферном давлении и температуре Т; С — универсальная константа (С = 0,0894); В(Т) —коэффициент зависимости удельного объема от температуры.
Применение уравнения Тейта к данным по сжимаемости расплавов аморфных полимеров также дает хорошие результаты. Значение Vo(Т) легко рассчитывается из уравнения, если известно значение V (Р,Т) при каких-нибудь температуре и давлении, отличных от нормальных.
_______________
*Питер Тейт (англ. Peter Guthrie Tait, 1831–1901) - шотландский математик и физик, один из основоположников термодинамики.
Слайд 53Термодинамическое уравнение состояния
Классическая термодинамика, используя представление о связи давления с изменением внутренней
Термодинамическое уравнение состояния
Классическая термодинамика, используя представление о связи давления с изменением внутренней

уравнение можно записать в виде:
Поскольку
Используя полученное Франком выражение для внутренней энергии:
и известное из статической физики соотношение
где N — число Авогадро*, k — постоянная Больцмана**, R —универсальная газовая постоянная), получим:
Если параметр n = 0, то уравнение превращается в известное уравнение состояния для идеального газа. Если n = 1, то уравнение превращается в уравнение Ван-дер-Ваальса:
__________________________________________
*Амедо Авогaдро (итал. Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e Cerreto; 1776 — 1856) — итальянский учёный-химик, первооткрыватель фундаментального физико-химического закона, названного его именем.
** Людвиг Больцман (нем. Ludwig Eduard Boltzmann; 1844 — 1906) — австрийский физик-теоретик, основатель статистической механики и молекулярно-кинетической теории.
Слайд 54Уравнение состояния Спенсера–Джилмора (Spencer-Gilmore equation)
Пытаясь обобщить известные экспериментальные данные по сжимаемости и
Уравнение состояния Спенсера–Джилмора (Spencer-Gilmore equation)
Пытаясь обобщить известные экспериментальные данные по сжимаемости и

Здесь V — удельный объём полимера; Μ — молекулярная масса структурной единицы, обусловливающей межмолекулярное взаимодействие; π и b — константы.
Если продифференцировать уравнение по переменной V, то после несложных преобразований получим:
Изменение объёма может происходить при постоянном давлении или постоянной тем-пературе. Такие изменения характеризуются коэффициентом сжимаемости β и терми-ческим коэффициентом линейного расширения λ, в общем случае зависящими от давления и температуры:
Дифференцируя уравнение Тейта можно получить следующие выражения для β и λ:
1 — полиэтилен высокой плотности; 2— полистирол;
3 — полиэтилен низкой плотности; 4 — полиамид.
Слайд 55ТЕПЛООБМЕН
Различают три вида теплообмена:
теплопроводность,
теплопередача конвекцией
лучистый теплообмен.
Передача тепла за счёт
ТЕПЛООБМЕН
Различают три вида теплообмена:
теплопроводность,
теплопередача конвекцией
лучистый теплообмен.
Передача тепла за счёт

При конвекции, которая возможна только в жидкостях и газах, тепло передается за счёт относительного движения частиц нагретого тела.
При лучистом теплообмене передача тепла между пространственно разделенными частями тела происходит за счёт электромагнитного излучения.
Слайд 56ТЕПЛОПРОВОДНОСТЬ
Основной задачей теории теплопроводности является установление распределения температур внутри тела.
Передача тепла происходит
ТЕПЛОПРОВОДНОСТЬ
Основной задачей теории теплопроводности является установление распределения температур внутри тела.
Передача тепла происходит

где q — количество тепла, проходящего через единичную поверхность, перпендикулярную направлению теплового потока;
k — коэффициент теплопроводности.
Уравнение теплопроводности для изотропного твердого тела:
Если внутри изотропного тела имеется источник тепла, то уравнение необходи-мо дополнить членом, учитывающим тепловыделение:
где а = k/ρCp — коэффициент температуророводности
(замена Cv на Ср в уравнении возможна для несжимаемых твердых тел);
2 — оператор Лапласа в прямоугольной системе координат
Значение оператора Лапласа в точке может быть истолковано
как плотность источников потенциального векторного поля в этой точке.
___________________________
* Барон Жан-Батист Жозеф Фурье (фр.Jean-Baptiste Joseph Fourier; 1768—1830) — французский математик и физик.
G — интенсивность внутренних тепловыделений, отнесенная к единице объема
Слайд 57Теплопередача в стационарном режиме.
Теплопередачу в непрерывно действующих нагревательных системах перерабатывающего оборудования
Теплопередача в стационарном режиме.
Теплопередачу в непрерывно действующих нагревательных системах перерабатывающего оборудования

Нестационарная теплопроводность.
В большинстве случаев в реальных процессах переработки приходится иметь дело с нестационарным режимом теплопроводности.
Теоретические исследования процесса нестационарной теплопроводности представляют собой обширный раздел математической физики. Решения, получаемые в результате интегрирования уравнения представляют собой функции времени и пространственных координат, удовлетворяющие начальным и граничным условиям.
Различают четыре рода граничных условий:
Первого рода - задано распределение температур на поверхности:T(t, L) = T(L)
Второго рода - задана плотность теплового потока для каждой точки поверхности тела как функция времени:
Третьего рода - задан коэффициент теплообмена α на границе и температура контактирующей с граничной поверхностью среды Tf:
Четвертого рода – задан теплообмен тела с окружающей средой. Температура соприкасающихся поверхностей одинакова: Tn(t) = Tc(t)
Слайд 58ТЕПЛОПЕРЕДАЧА В ПОТОКАХ РАСПЛАВА
Передача тепла в движущейся жидкости происходит по механизму конвективного
ТЕПЛОПЕРЕДАЧА В ПОТОКАХ РАСПЛАВА
Передача тепла в движущейся жидкости происходит по механизму конвективного

Аналитическое решение дифференциальных уравнений теплопроводности в случае конвективного теплообмена удается получить лишь при введении большого числа упрощений. Поэтому для практических целей используют результаты экспериментальных исследований, представленные в виде зависимостей между соответствующими критериями подобия
Обычно при изучении теплопередачи конвекцией принимаются следующие допущения:
1) на границе с поверхностью нагрева (охлаждения) соблюдаются условия прилипания;
2) физические параметры жидкости (теплоёмкость, теплопроводность, плотность и вязкость) сохраняют неизменное значение для всего потока;
3) лучистый теплообмен между поверхностью нагрева и потоком жидкости происходит независимо от контактной теплоотдачи.
Для описания процесса теплообмена обычно используется известное уравнение Ньютона: q = α(Tw — TЖ)
где α = λ/ δ — коэффициент теплоотдачи, определяющий количество тепла, подводимое к жидкости в единицу времени через поверхность с единичной площадью δ;
Tw — температура стенки канала; Тж — средняя температура жидкости.
Слайд 59Использование методов теории подобия позволяет свести решение проблемы теплообмена в потоке жидкости
Использование методов теории подобия позволяет свести решение проблемы теплообмена в потоке жидкости

Nu = αd/ λ - критерий Нуссельта, характеризующий интенсивность теплообмена.
Эрнст Крафт Вильгельм Нуссельт (нем. Ernst Kraft Wilhelm Nußelt 1882 — 1957 ) — немецкий инженер-исследователь
Рr = εΡμ/λ — критерий Прандтля, характеризующий соотношение между количест-вом тепла, поглощаемого жидкостью за счёт изменения энтальпии, и количеством тепла, отводимого за счет теплопроводности
Людвиг Прандтль (нем. Ludwig Prandtl 1875 — 1953 ) немецкий механик и физик
Gr = gλP2l3ΔT/μ2 - критерий Грасгофа, характеризующий интенсивность тепло-обмена за счёт свободной конвекции.
Франц Грасгоф, (нем. Franz Grashof; 1826 — 1893) — немецкий механик и машиностроитель
Re = vlp/μ — число Рейнольдса, характеризующее отношение сил инерции к силам вязкого трения
Осборн Рейнольдс (англ. Osborne Reynolds; 1842 —1912) английский механик, физик и инженер, специалист в области гидромеханики и гидравлики)
Ре = vd/a — критерий Пекле. При малых значениях преобладает молекулярная теплопроводность, а при больших — конвективный перенос теплоты. Число Пекле связано соотношением с числом Рейнольдса и числом Прандтдя Ре = Re· Рr
Жан Клод Эжен Пекле (фр. J. С. Péclet,) 1793—1857.
Gz = wCp/ λl —критерий Гретца, безразмерная единица потока тепла.
Лео Гретц (нем. Leo Graetz 1856 — 1941) - немецкий физик.
Слайд 60 Известные в настоящее время результаты экспериментального исследования теплообмена в расплавах полимеров относятся
Известные в настоящее время результаты экспериментального исследования теплообмена в расплавах полимеров относятся

Общая формула имеет вид:
Индексы «ж» и «ст» означают, что соответствующие значения критерия относятся к усредненным характеристикам жидкости или к характеристикам жидкости в пристенном слое.
Слайд 61ЛУЧИСТЫЙ ТЕПЛООБМЕН
Лучистая энергия передается в виде электромагнитных волн, распростра-няющихся в пространстве до
ЛУЧИСТЫЙ ТЕПЛООБМЕН
Лучистая энергия передается в виде электромагнитных волн, распростра-няющихся в пространстве до

Излучаемая энергия пропорциональна четвертой степени абсолютной температуры изучающего тела. Так как обычно большая часть энергии излуче-ния в применяемой на практике области температур приходится на инфракрасный спектр, нагрев излучением называют также инфракрасным нагревом.
Гипотетическое тело, поглощающее все падающие на него лучи, называется абсолютно чёрным телом.
Интенсивность лучеиспускания абсолютно чёрного тела Еb определяется законом Стефана*— Больцмана: Eb=σ·T4,
σ — постоянная Стефана-Больцмана, равная 1,36·10-12 кал/(см2·с·К4) / 3,65·10-8 Вт/м2·с·К4
Реальные тела поглощают только часть попадающего на них излучения.
Их излучательная способность Ɛ оценивается по формуле: Ɛ =Е / Eb ,
где Ε — интенсивность лучеиспускания реального тела.
Обычно Ɛ зависит от температуры, увеличиваясь с её ростом.
Металлы и их окислы обладают высокой излучательной способностью (ε ≥0,8).
У хорошо отполированных металлов излучательная способность невысока (ε ≤0,1).
Коэффициент поглощения определяется как отношение поглощенного излучения к падающему.
_____________________________
* Йозеф Стефан (словен. Jožef Stefan, нем. Joseph Stefan, 1835—1893) — австрийско-словенский физик и математик.
Слайд 62 При расчете лучистого теплообмена между чёрными телами под излучение попадает только та
При расчете лучистого теплообмена между чёрными телами под излучение попадает только та

Можно учесть взаимное расположение излучателя и облучаемого тела введением коэффициента видимости, учитывающего долю излучаемой энергии, которая попадает на облучаемое тело.
Для неабсолютно чёрных тел расчёт осложняется наличием доли много-кратно отраженного излучения.
Реальные полимеры и их расплавы плохо пропускают инфракрасное излучение. Поэтому падающая на них энергия превращается в тепло непосредст-венно на их поверхности. Некоторое количество выделяющегося тепла сразу же теряется на потери в виде собственного излучения и путем конвекции.
Поглощаемое тепло распространяется внутрь за счет процессов теплопро-водности. Поэтому итоговое распределение температур в теле, нагреваемом лучистой энергией, зависит не только от мощности потока лучистой энергии, но также и от теплопроводности и конвективных потерь.
Слайд 63СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ О МЕХАНИЗМЕ СТРУКТУРООБРАЗОВАНИЯ
В ПРОЦЕССАХ ПЕРЕРАБОТКИ
ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ КИНЕТИКИ КРИСТАЛЛИЗАЦИИ
Из теории
СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ О МЕХАНИЗМЕ СТРУКТУРООБРАЗОВАНИЯ
В ПРОЦЕССАХ ПЕРЕРАБОТКИ
ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ КИНЕТИКИ КРИСТАЛЛИЗАЦИИ
Из теории

Описывает процесс фазового перехода при постоянной температуре.
Изначально оно было получено для случая кристаллизации расплавов в 1937 году А. Н. Колмогоровым*, и независимым образом в 1939 году Р. Ф. Мелом (Robert Franklin Mehl ) и У. Джонсоном (W. A. Johnson), а также было популяризировано в серии статей
М. Аврами (М. Avrami) в 1939-1941 годах. Формула может быть обобщена на случаи разных фазовых переходов: ln θ = —k ·t m
где k — константа скорости; m — параметр, значение которого, выраженное целыми числами, соответствует природе центров кристаллизации и характеру их роста:
Тип роста Образование центров кристаллизации m
Линейный Непрерывное 1
(одномерный) Спорадическое 2
Пластинчатый Непрерывное 2
(двухмерный) Спорадическое 2
Сферический Непрерывное 3
(трехмерный) Спорадическое 4
___________________________
*Андрей Николаевич Колмогоров
(1903 — 1987) — русский советский
математик, один из крупнейших
математиков XX века. Один из
основоположников современной
теории вероятностей, им получены фундаментальные результаты
топологии, геометрии, матема-
тической логике, классической механике, теории турбулентности, теории сложности алгоритмов, теории информации, теории тригонометрических рядов, теории меры, теории приближения функций, теории множеств, теории дифференциальных уравнений, теории динамических систем, фунциональ- ном анализе.
Слайд 64Образование упорядоченных структур благодаря более компактной упаковке сопро-вождается одновременным уменьшением удельного объема.
Образование упорядоченных структур благодаря более компактной упаковке сопро-вождается одновременным уменьшением удельного объема.

Если ΔV∞ — изменение объёма при полной кристаллизации, а ΔVt — текущее изменение объёма, то отношение ΔV∞/ ΔVt определяет текущее значение степени кристаллизации. Остаточная доля незакристаллизовавшегося полимера определится выражением θ =1— ΔV∞/ΔVt .
Типичная зависимость lg θ от времени для процесса
кристаллизации полипропилена при температуре
401К приведена на рисунке:
Если прологарифмировать уравнение Колмогорова—Аврами, то полученный результат будет представлять прямую линию при условии, что m не зависит от t:
Результаты обработки данных для временной зависимости процесса кристаллизации полиэтилентерефталата приведены на рисунке, из которого видно, что m зависит от температуры. Это связано с тем, что при изменении тем-пературы меняется механизм кристаллизации. Так, при низких температурах формируются преимущественно линейные структуры, соответственно m=2. При более высокой температуре идет спорадическое формирование сферических структур, m = 4.
Слайд 65 Обычно в качестве характеристики температурной зависимости константы скорости кристаллизации используют значения не
Обычно в качестве характеристики температурной зависимости константы скорости кристаллизации используют значения не
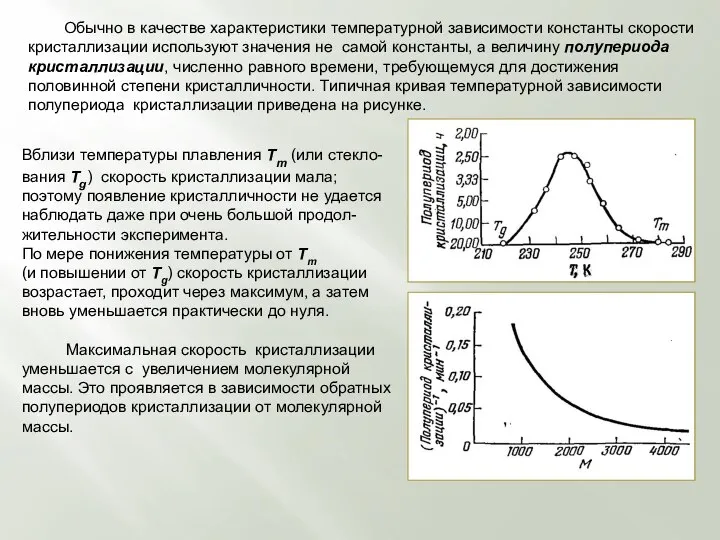
Вблизи температуры плавления Тm (или стекло-вания Tg) скорость кристаллизации мала; поэтому появление кристалличности не удается наблюдать даже при очень большой продол-жительности эксперимента.
По мере понижения температуры от Тm
(и повышении от Tg) скорость кристаллизации возрастает, проходит через максимум, а затем вновь уменьшается практически до нуля.
Максимальная скорость кристаллизации уменьшается с увеличением молекулярной массы. Это проявляется в зависимости обратных полупериодов кристаллизации от молекулярной массы.
Слайд 66ВЛИЯНИЕ ТЕМПЕРАТУРЫ И СКОРОСТИ ОХЛАЖДЕНИЯ НА КРИСТАЛЛИЗАЦИЮ
ВЛИЯНИЕ ТЕМПЕРАТУРЫ И СКОРОСТИ ОХЛАЖДЕНИЯ НА КРИСТАЛЛИЗАЦИЮ

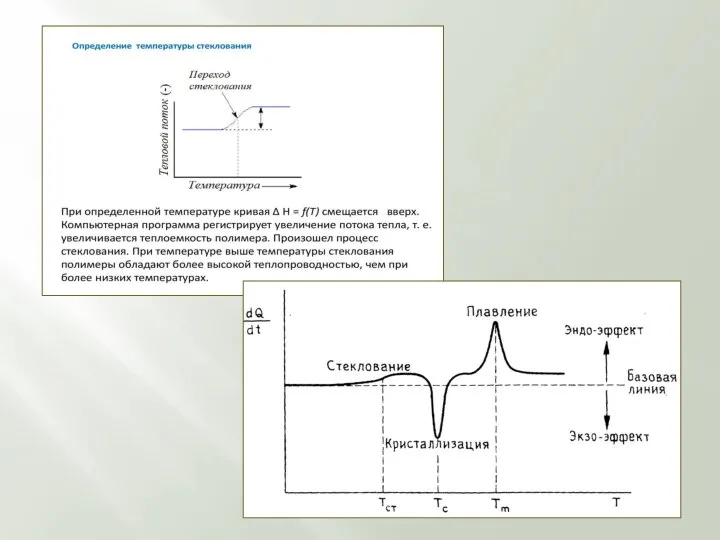
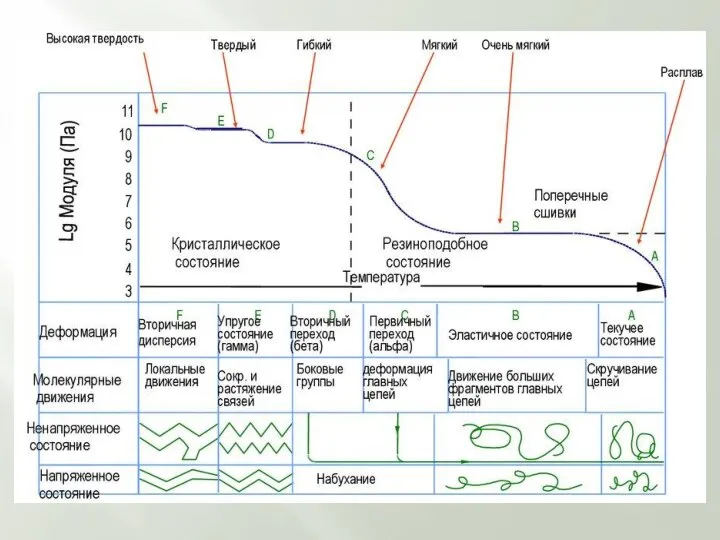
 Амины. Способы получения
Амины. Способы получения Вода - растворитель
Вода - растворитель Юный химик. Интерактивная интеллектуальная игра
Юный химик. Интерактивная интеллектуальная игра Кремень. Нахождение в природе
Кремень. Нахождение в природе Углеводороды. Алканы
Углеводороды. Алканы Металлы d-элементы
Металлы d-элементы Водородная химическая связь
Водородная химическая связь Природные и искусственные материалы. Естествознание. 6 класс
Природные и искусственные материалы. Естествознание. 6 класс Чистячі засоби для ванної кімнати та кафелю
Чистячі засоби для ванної кімнати та кафелю Презентация Лекция 1. Химическая термодинамика
Презентация Лекция 1. Химическая термодинамика Анилин (амидобензол, аминобензол, фениламин)
Анилин (амидобензол, аминобензол, фениламин) Сахароза, крахмал, целлюлоза
Сахароза, крахмал, целлюлоза Синтетические душистые вещества
Синтетические душистые вещества Фізика гірських порід і процесів. Хімічні зв'язки в мінералах. Іонний зв'язок
Фізика гірських порід і процесів. Хімічні зв'язки в мінералах. Іонний зв'язок Презентация на тему Классификация полимеров
Презентация на тему Классификация полимеров  Магний (Mg)
Магний (Mg) Презентация на тему Физические и химические явления 8 класс
Презентация на тему Физические и химические явления 8 класс  Селективное каталитическое восстановление оксидов азота
Селективное каталитическое восстановление оксидов азота Презентация на тему Химические реакции
Презентация на тему Химические реакции  Презентация по Химии "Алмаз"
Презентация по Химии "Алмаз"  Сравнительный анализ Фармакопейных статей для субстанций, представленных в мировых Фармакопеях
Сравнительный анализ Фармакопейных статей для субстанций, представленных в мировых Фармакопеях Общие сведения о питании и приготовлении пищи
Общие сведения о питании и приготовлении пищи Кислоты
Кислоты Металлы. Определения
Металлы. Определения Indikatori. R. Boila eksperiments
Indikatori. R. Boila eksperiments Предельные углеводороды. Алканы (1)
Предельные углеводороды. Алканы (1) Алкины и их свойства
Алкины и их свойства Химическая кинетика. Факторы, влияющие на скорость реакции
Химическая кинетика. Факторы, влияющие на скорость реакции