Содержание
- 2. 1. Привести к стандартному виду: 2. Слагаемые с переменной оставить в левой части, без переменной перенести
- 3. Примеры
- 4. Алгоритм решения квадратных уравнений Привести к стандартному виду: Найти дискриминант по формуле: Записать ответ.
- 5. Алгоритм решения линейных неравенств 1.Привести к стандартному виду: Или 2. Слагаемые с переменной оставить в левой
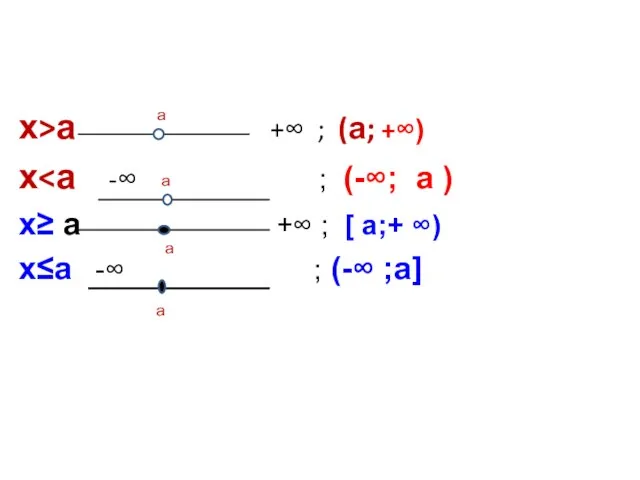
- 6. х>а +∞ ; (а; +∞) х х≥ а +∞ ; [ а;+ ∞) х≤а -∞ ;
- 7. Примеры
- 8. Алгоритм решения квадратных неравенств Привести к стандартному виду: Приравнять к нулю левую часть: Найти корни, получившегося
- 9. Примеры -6 4 + + -
- 12. Скачать презентацию







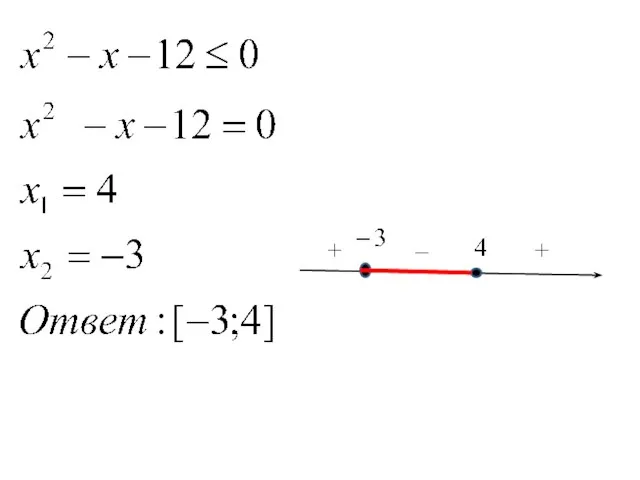
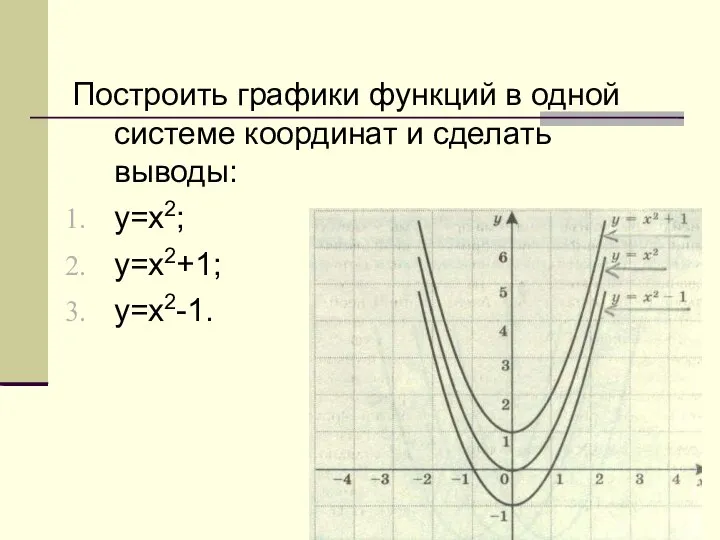 Преобразования графика квадратичной функции. Преобразования графика
Преобразования графика квадратичной функции. Преобразования графика Состав числа. Тренажер. Старшая группа
Состав числа. Тренажер. Старшая группа Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Квадратные неравенства с параметрами
Квадратные неравенства с параметрами Задача на движение
Задача на движение Множества. 8 класс
Множества. 8 класс Рисование по координатам
Рисование по координатам Презентация на тему Итоговое повторение курса алгебры за 8 класс
Презентация на тему Итоговое повторение курса алгебры за 8 класс  Окружность. Повторение
Окружность. Повторение Домашнее задание по геометрии
Домашнее задание по геометрии Графы. ЕГЭ задание 15. Урок 11 А
Графы. ЕГЭ задание 15. Урок 11 А Статистическая радиотехника. Случайный процесс, ансамбль его реализаций
Статистическая радиотехника. Случайный процесс, ансамбль его реализаций Рациональные приемы вычислений
Рациональные приемы вычислений Вставь пропущенные числа
Вставь пропущенные числа Решение задач на концентрацию при подготовке к ГИА
Решение задач на концентрацию при подготовке к ГИА Степень с натуральным показателем
Степень с натуральным показателем Обратные тригонометрические функции
Обратные тригонометрические функции Квадратные уравнения
Квадратные уравнения Расстояние между двумя точками. 9 класс
Расстояние между двумя точками. 9 класс Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Первообразная и интеграл
Первообразная и интеграл 1_теория множеств
1_теория множеств День таблицы умножения
День таблицы умножения Показательные неравенства
Показательные неравенства Задачи на построение треугольника
Задачи на построение треугольника Блиц-турнир
Блиц-турнир Презентация на тему Двугранный угол
Презентация на тему Двугранный угол  Описанная окружность. 8 класс
Описанная окружность. 8 класс