ДУ и численные методы. Системы дифференциальных уравнений. 2 семестр. Лекция 8

Введение
Во многих задачах математики, физики и техники требуется определить несколько функций, связанных между собой несколькими дифференциальными уравнениями.
Для этого необходимо располагать, вообще говоря, таким же числом уравнений. Если каждое из этих уравнений является дифференциальным, то есть имеет вид соотношения, связывающего неизвестные функции и их производные, то говорят о системе дифференциальных уравнений.

Основные понятия теории СДУ
Определение. Система уравнений вида
связывающих независимую переменную t, неизвестные функции и их производные до порядков m1,m2,… mk соответственно, называется системой обыкновенных дифференциальных уравнений в общей форме.
Сумма порядков старших производных неизвестных функций, входящих в СДУ, называется порядком СДУ.

Определение. Совокупность непрерывно дифференцируемых на (а,b)
функций
называется решением СДУ, если она обращает на интервале (а,b) каждое уравнение этой системы в тождество.

Способы представления СДУ
1. Канонический вид.

2. Нормальный вид.
Замечание:
Для неизвестных функций
y1(x), y2(x),…, yn(x) СДУ
примет вид:

Если СДУ задана в канонической форме, то ее можно записать в нормальной форме, обозначив производные искомых функций через дополнительные неизвестные функции.
Пример: записать СДУ в нормальной форме.
Обозначим , тогда .

Геометрическая интерпретация СДУ в нормальной форме
Рассмотрим для определенности нормальную систему:
Общее решение этой системы имеет вид:
Каждая из функций - уравнение цилиндрической поверхности в трехмерном пространстве,
их совокупность – кривую в Oxyz, которая является интегральной кривой исходной системы.

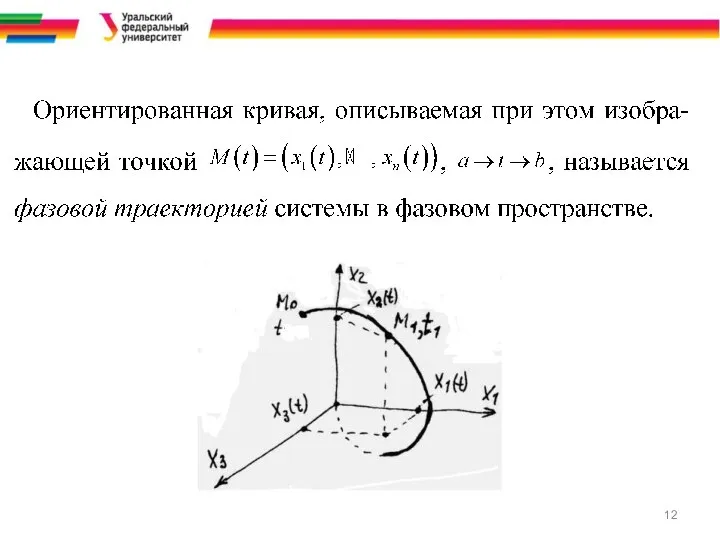
Механическая интерпретация СДУ в нормальной форме

Некоторые приемы аналитического решения СДУ
Сведение к одному уравнению (исключения неизвестных)
или в векторном виде

Пример. Найти общее решение системы уравнений:
Продифференцируем первое уравнение:
Подставим в это выражение производную у′ =2x + 2y из второго уравнения.
Подставим сюда у, выраженное из первого уравнения:
Получим ОЛДУ:

Домашнее задание
Решить СДУ сведением к одному ДУ