Слайд 2Если хочешь научиться плавать
-смело входи в воду.
Если хочешь научиться решать
задачи - решай

их!
Д. Пойа
Слайд 3Решение
1) АВ=ВС=АС, так как треугольник АВС равносторонний
2) АС = 2⋅8= 16
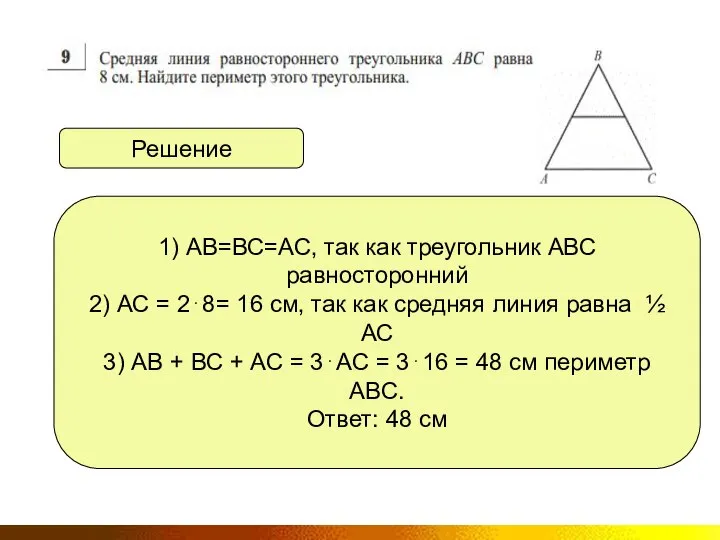
см, так как средняя линия равна ½ АС
3) АВ + ВС + АС = 3⋅АС = 3⋅16 = 48 см периметр АВС.
Ответ: 48 см
Слайд 4Решение
1) Пусть О - точка пересечения
диагоналей прямоугольника.
Диагонали прямоугольника равны,
в
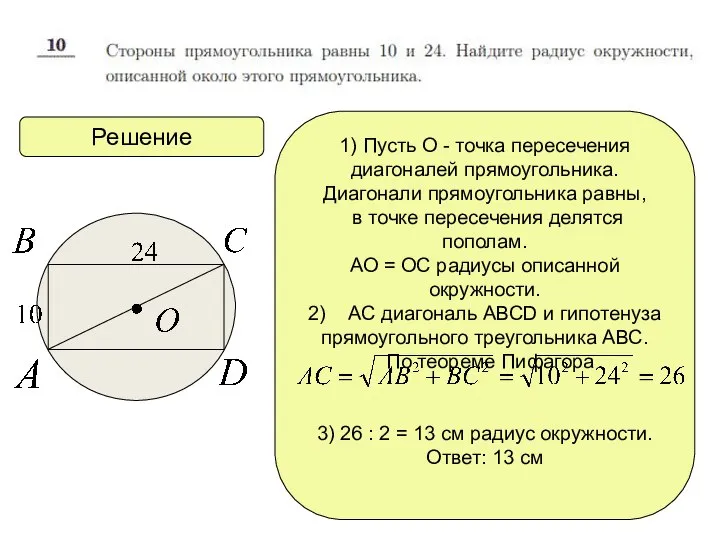
точке пересечения делятся пополам.
АО = ОС радиусы описанной окружности.
2) АС диагональ АВСD и гипотенуза
прямоугольного треугольника АВС.
По теореме Пифагора
3) 26 : 2 = 13 см радиус окружности.
Ответ: 13 см
Слайд 5Решение
1) Площадь квадрата равна квадрату его стороны.
Обозначим сторону квадрата за

х. По теореме Пифагора
Найдём площадь квадрата
Ответ:
Слайд 6Решение:
1. Достроим до прямоугольника АВСD и проведём диагонали,
О- точка пересечения диагоналей

АС и ВD.
АО=ОС=ОВ=ОD по свойству диагоналей прямоугольника.
2. АО медиана и АО = ½ ВD. По теореме Пифагора
Ответ: 2,5
Слайд 8 Решение:
Точка О - центр описанной окружности и середина гипотенузы
прямоугольного

треугольника. По теореме Пифагора
Ответ: 6,5
Слайд 9Решение:
ВН – медиана треугольника АВС и его высота, тогда
треугольник АВС равнобедренный

( из равенства
треугольников АВН и СВН). ВС=АВ=2⋅3=6.
О – точка пересечения медиан СМ и ВН.
ВО:ОН=СО:ОМ (по св-ву медианы тр-ка). ∠ МОС= ∠ВОС, так как
вертикальные. Значит ∆МОС∞∆СОВ по второму признаку
подобия треугольников .
Поэтому .
Ответ: 3
Слайд 10Решение:
По теореме Пифагора найдём гипотенузу
прямоугольного треугольника : .
Косинус угла равен

4:5=0,8
По формуле приведения ,
поэтому косинус угла на рисунке будет равен -0,8.
Ответ: -0,8
Слайд 11 Решение:
∠АОВ вписан в окружность
и опирается на дугу равную
60 градусам
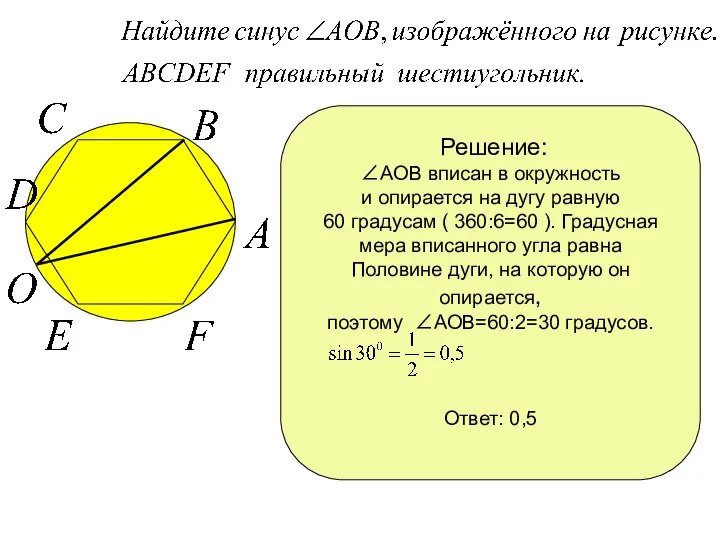
( 360:6=60 ). Градусная
мера вписанного угла равна
Половине дуги, на которую он опирается,
поэтому ∠АОВ=60:2=30 градусов.
Ответ: 0,5
Слайд 12Творческих успехов,
уважаемые коллеги!











 Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Неопределённый и определённый интеграл
Неопределённый и определённый интеграл Веселый паровоз. Мультимедийное пособие по математике
Веселый паровоз. Мультимедийное пособие по математике Проект Колодец. Деловая игра по теме Цилиндр
Проект Колодец. Деловая игра по теме Цилиндр Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел 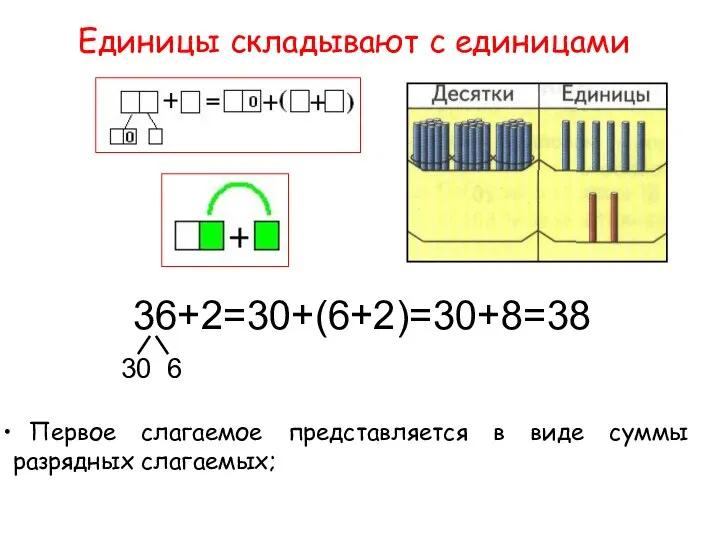 Алгоритм вычислений
Алгоритм вычислений Логика
Логика Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8
Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8 Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Пирамида. Виды пирамид
Пирамида. Виды пирамид Игра-тренажёр Округление чисел
Игра-тренажёр Округление чисел Вычисление одномерных, двумерных и интегралов c переменным верхним пределом
Вычисление одномерных, двумерных и интегралов c переменным верхним пределом Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.)
Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.) Правильные многогранники
Правильные многогранники Алгебраические выражения
Алгебраические выражения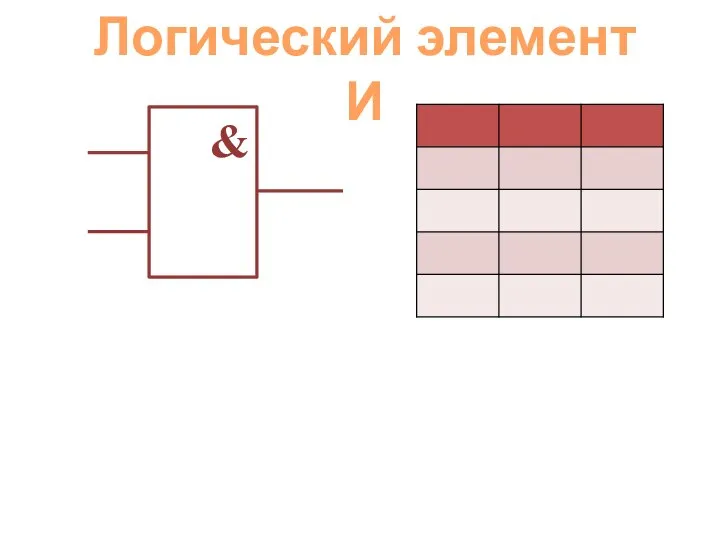 Логический элемент
Логический элемент Презентация на тему Вектор
Презентация на тему Вектор  Правила с двумя решениями. Подход Неймана – Пирсона
Правила с двумя решениями. Подход Неймана – Пирсона Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»
Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2» Презентация на тему Отрезок. Графики
Презентация на тему Отрезок. Графики  Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Окружность. 5 класс
Окружность. 5 класс Урок 14. Первый признак равенства треугольников
Урок 14. Первый признак равенства треугольников Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс)
Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс) Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)  Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Тестирование генераторов случайных чисел
Тестирование генераторов случайных чисел Презентация на тему Подготовка к ГИА 2013
Презентация на тему Подготовка к ГИА 2013