Содержание
- 2. Изучение нового материала r = 1 r = 2 где r = -1 r = 1
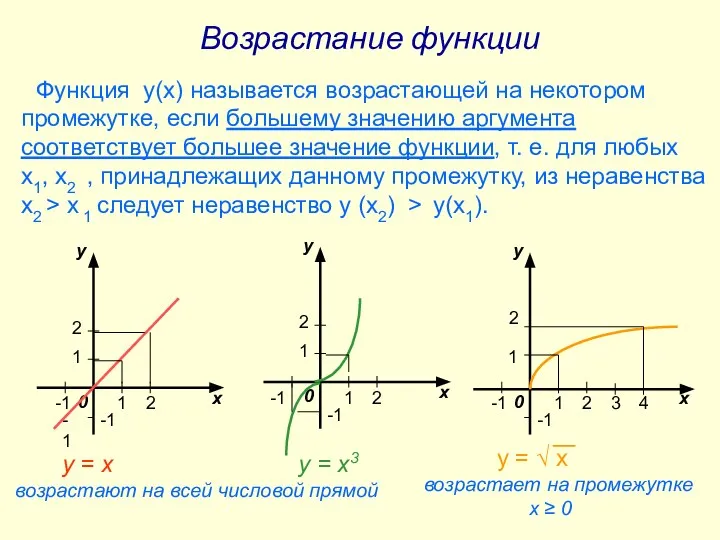
- 3. Возрастание функции Функция у(х) называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение
- 4. Убывание функции Функция у(х) называется убывающей на промежутке, если большему значению аргумента соответствует меньшее значение функции,
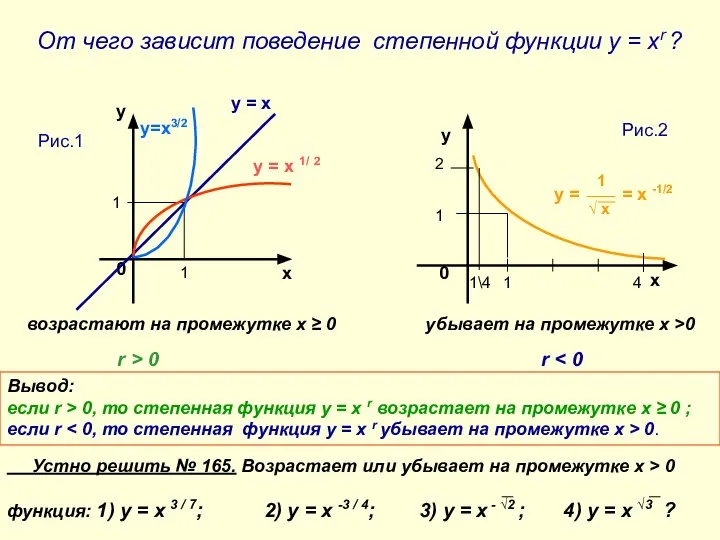
- 5. От чего зависит поведение степенной функции у = хr ? возрастают на промежутке х ≥ 0
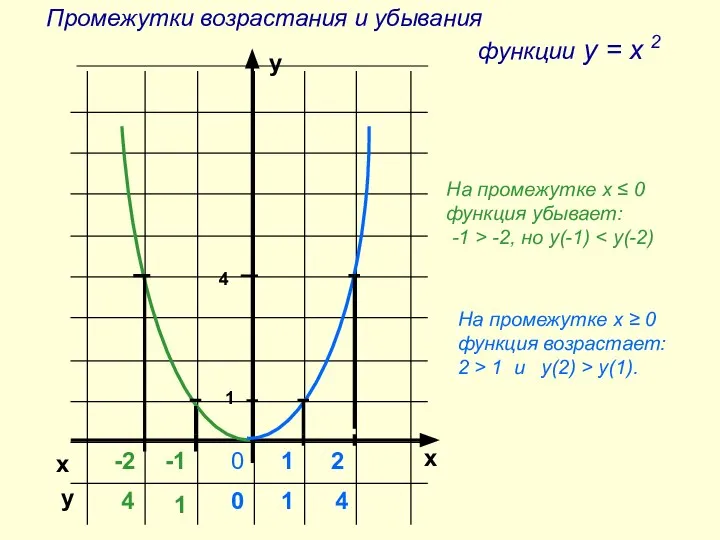
- 6. Промежутки возрастания и убывания функции у = х 2 На промежутке х ≤ 0 функция убывает:
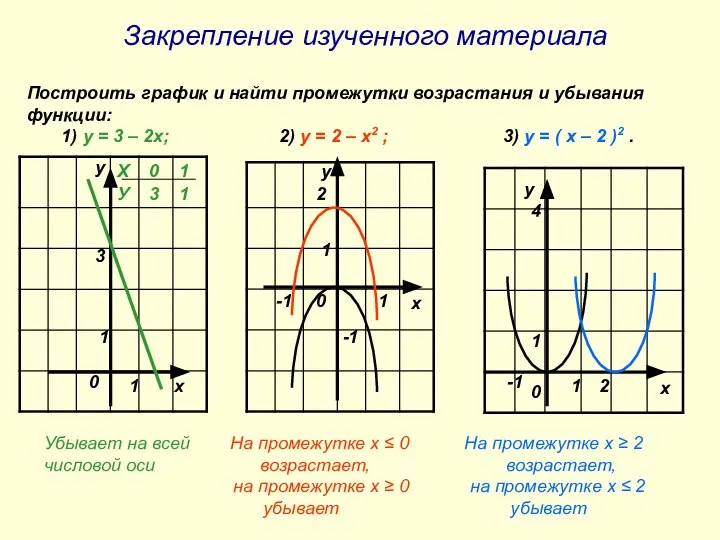
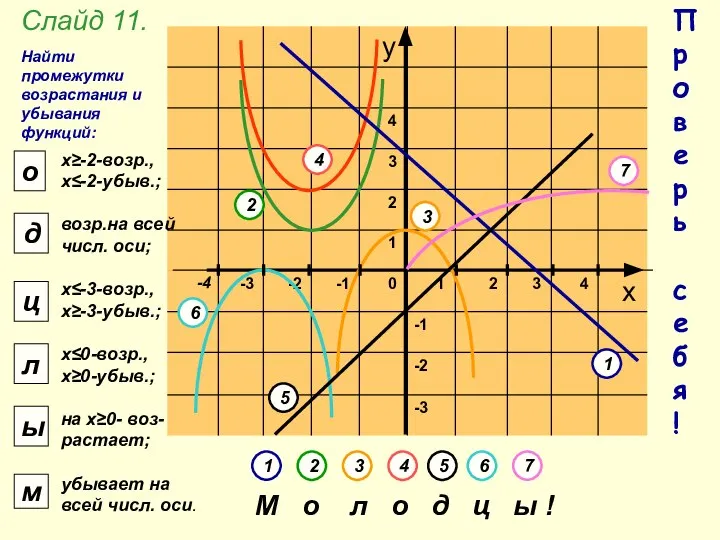
- 7. Закрепление изученного материала Построить график и найти промежутки возрастания и убывания функции: 1) у = 3
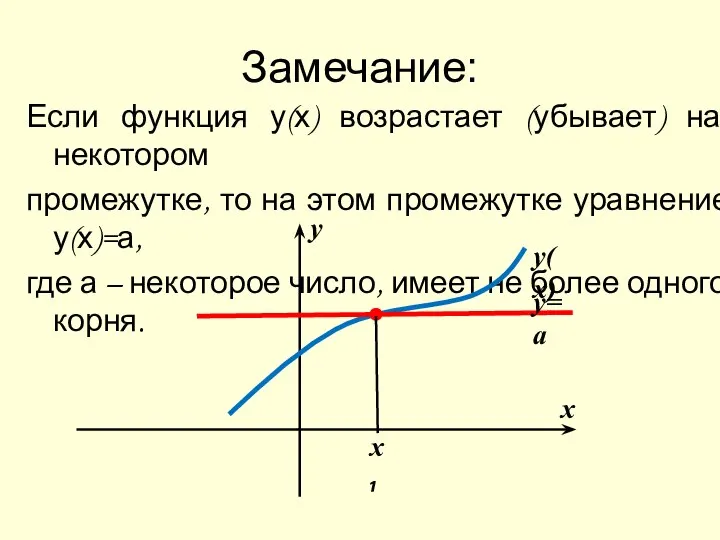
- 8. Замечание: Если функция у(х) возрастает (убывает) на некотором промежутке, то на этом промежутке уравнение у(х)=а, где
- 9. Решение уравнений вида хr =a Функция вида у=хr называется …. При r>0 функция…. При r Значит
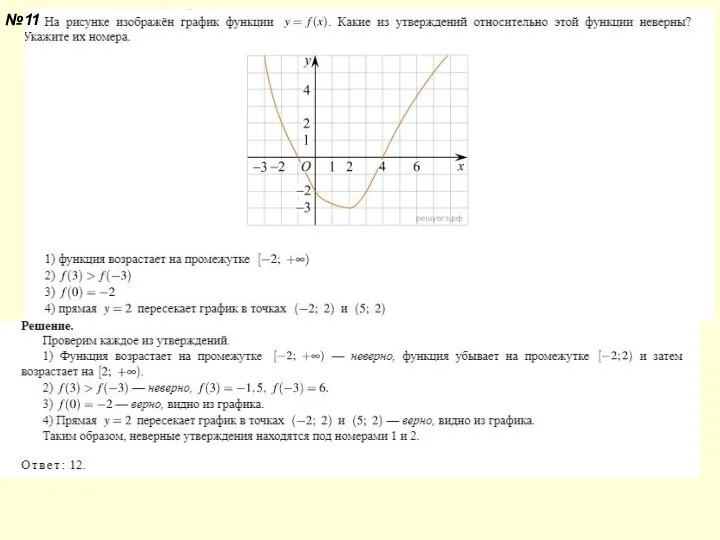
- 10. №11
- 14. 6 3 2 1 5 4 П р о в е р ь с е б
- 16. Скачать презентацию





 Среднее арифметическое. Размах. Мода
Среднее арифметическое. Размах. Мода Векторная алгебра
Векторная алгебра Презентация на тему Формулы (5 класс)
Презентация на тему Формулы (5 класс)  Презентация на тему Исследование функции с помощью производной
Презентация на тему Исследование функции с помощью производной  Аксиомы стереометрии
Аксиомы стереометрии Оператор Лапласа в полярных, цилиндрических и сферических системах координат
Оператор Лапласа в полярных, цилиндрических и сферических системах координат Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7
Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7 Виды четырехугольников
Виды четырехугольников Цилиндр
Цилиндр Симметрия вокруг нас
Симметрия вокруг нас Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла Метод координат в пространстве
Метод координат в пространстве Презентация на тему Правила дифференцирования
Презентация на тему Правила дифференцирования  Состав числа 8
Состав числа 8 Учимся писать цифры
Учимся писать цифры Длина окружности и число пи
Длина окружности и число пи Геометрия, как наука
Геометрия, как наука Чётные и нечётные числа. Подготовка к контрольной работе
Чётные и нечётные числа. Подготовка к контрольной работе Многозначная логика
Многозначная логика Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1) Вычислительная математика. Практика №1
Вычислительная математика. Практика №1 Координатная плоскость. Графики
Координатная плоскость. Графики Уравнение прямой
Уравнение прямой Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Теорема Фалеса
Теорема Фалеса Решение уравнений. Тест
Решение уравнений. Тест Методы многокритериальной оптимизации
Методы многокритериальной оптимизации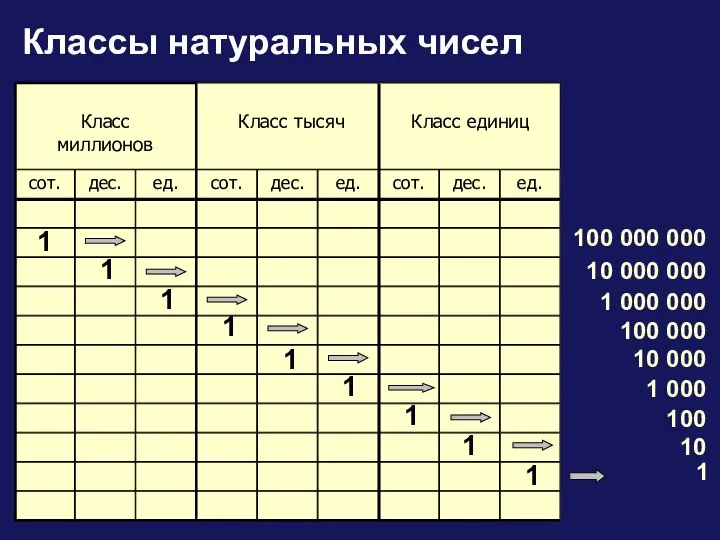 Классы натуральных чисел
Классы натуральных чисел