Содержание
- 2. 1. Какую функцию называют квадратичной? 2. С помощью каких сдвигов вдоль координатных осей из графика функции
- 3. 19. 11. 18 Классная работа График функции у = ах 2 + bх + qс Работа
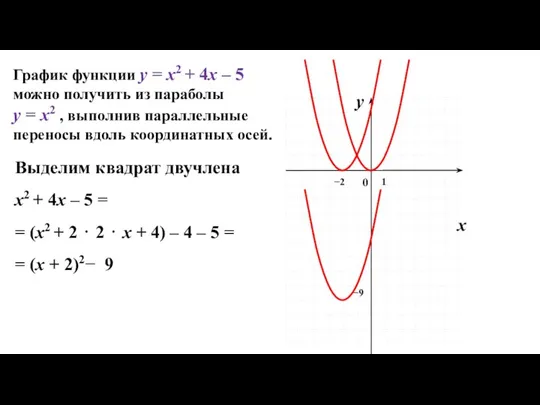
- 4. y х 0 1 График функции y = x2 + 4x – 5 можно получить из
- 5. Оказывается, для любой квадратичной функции верно утверждение: график функции у = ax2 + bx + c
- 7. Отсюда следует, что:
- 8. 1. Определить координату вершины параболы по формулам: 2. Отметить эту точку на координатной плоскости. 3. Через
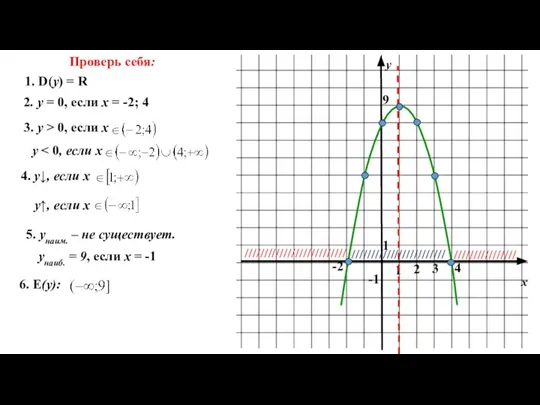
- 9. Постройте график функции у = -2х² + 2х + 8 и опишите его свойства Ось симметрии:
- 10. х у 1 1 4 2 3 -1 1. D(y) = R 2. у = 0,
- 11. № 263 (а, в) а) у = х2 - 4х + 2; в) у = 2х2
- 12. Работа с книгой: № 263 (а, в), № 264 (а; в), № 265 (а, в).
- 13. № 263 (а, в) а) у = х2 - 4х + 2; в) у = 2х2
- 14. Домашнее задание. n. 2.4; № 264 (б; г), № 265 (б; г).
- 16. Скачать презентацию







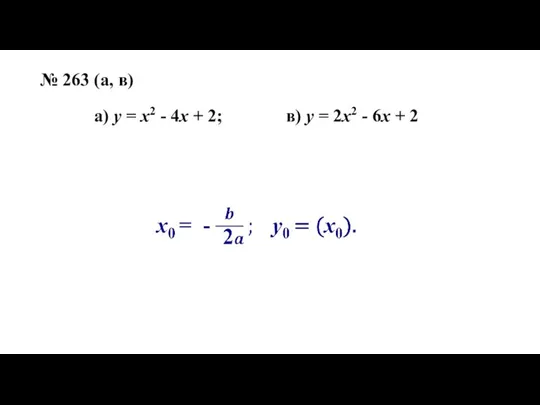



 1.6. Системы линейных алгебраических уравнений
1.6. Системы линейных алгебраических уравнений Перпендикуляр и наклонная
Перпендикуляр и наклонная Комбинированные уравнения. Задания для устного счета
Комбинированные уравнения. Задания для устного счета Преобразования графиков функций
Преобразования графиков функций Показательные уравнения
Показательные уравнения Вычислительная математика. Вычисление серии интегралов. Вычисление корней квадратного уравнения. Вычисление exp(x)
Вычислительная математика. Вычисление серии интегралов. Вычисление корней квадратного уравнения. Вычисление exp(x) Формирование счетных навыков. Требования к счетной деятельности
Формирование счетных навыков. Требования к счетной деятельности Подготовка к ГИА
Подготовка к ГИА Пирамида. Площадь поверхности пирамиды
Пирамида. Площадь поверхности пирамиды Задачи на разрезание
Задачи на разрезание itog-alg_8
itog-alg_8 Физический и геометрический смысл производной
Физический и геометрический смысл производной Прямая пропорциональность 7 класс 2012 год
Прямая пропорциональность 7 класс 2012 год Презентация на тему Многогранники. Призма
Презентация на тему Многогранники. Призма  ПГНИУ-20.09.22 МЛ Л 4
ПГНИУ-20.09.22 МЛ Л 4 Комбинаторика
Комбинаторика В гостях у деда. Аксиомы стереометрии
В гостях у деда. Аксиомы стереометрии Обобщающий урок по теме Многогранники
Обобщающий урок по теме Многогранники Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Рисуем параллелепипед
Рисуем параллелепипед Всероссийская олимпиада по функциональной грамотности Задания по математической грамотности
Всероссийская олимпиада по функциональной грамотности Задания по математической грамотности Занимательная математика
Занимательная математика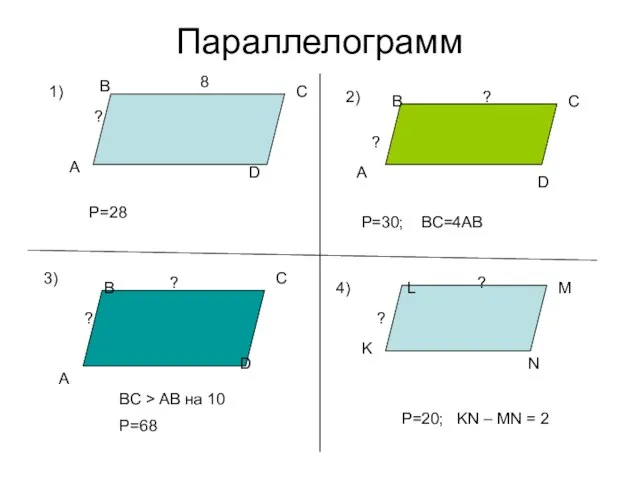 Параллелограмм
Параллелограмм Старинные меры длины
Старинные меры длины Признаки равенства треугольников
Признаки равенства треугольников Математический диктант выражениями в тетрадь
Математический диктант выражениями в тетрадь Использование логических операций в теории множеств. Инверсия
Использование логических операций в теории множеств. Инверсия