Игра Жизнь Conway's Game of Life

История «Conway's Game of Life»
В 1965 г. британский математик Джон Конвей заинтересовался проблемой, предложенной в 1940-х годах известным венгеро-американским математиком Джоном фон Нейманом, который пытался создать гипотетическую вычислительную машину, которая может воспроизводить сама себя.

История «Conway's Game of Life»
Конвей попытался упростить идеи, предложенные Нейманом, и в конце концов ему удалось создать правила, которые стали правилами математической игры (модели дискретного реального времени) «Жизнь».

История «Conway's Game of Life»
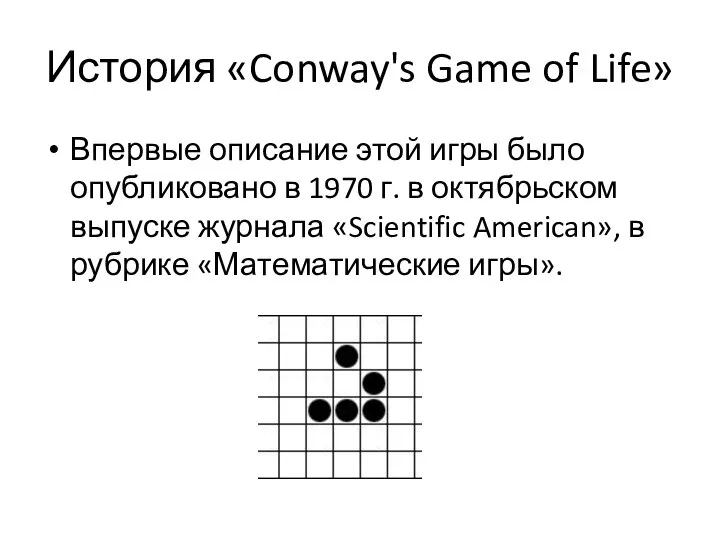
Впервые описание этой игры было опубликовано в 1970 г. в октябрьском выпуске журнала «Scientific American», в рубрике «Математические игры».

Правила «Conway's Game of Life»
Место действия игры— это разбитая на дискретные элементы (клетки) поверхность (2D-Вселенная): безграничная, ограниченная, конечная или замкнутая.
Чаще всего в качестве такой поверхности используют поверхность тора (ограниченная и замкнутая → компактная, но бесконечная).

Правила «Conway's Game of Life»
Каждая клетка на этой поверхности может находиться в двух состояниях: быть живой или быть мёртвой.
У каждой клетки есть восемь соседей.
Распределение живых клеток в начале игры называется первым поколением (оно может быть случайным или заданным).

Правила «Conway's Game of Life»
Каждое следующее поколение рассчитывается на основе предыдущего по трем правилам:
мёртвая клетка, рядом с которой находится ровно три живые клетки, оживает;
если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить;
если соседей у живой клетки меньше двух или больше трёх клетка умирает (от «одиночества» или от «перенаселённости», соответственно).

Правила «Conway's Game of Life»
Игрок не принимает прямого участия в игре, а лишь расставляет начальную конфигурацию «живых» клеток, которые затем взаимодействуют согласно правилам уже без его участия.
Эти простые правила приводят к огромному разнообразию «форм жизни», которые могут возникнуть в игре.

«Conway's Game of Life»
Вскоре после опубликования правил, было обнаружено несколько интересных шаблонов (вариантов расстановки живых клеток в первом поколении).
Некоторые такие фигуры остаются неизменными во всех последующих поколениях, состояние других периодически повторяется, в некоторых случаях со смещением всей фигуры.
Существует фигура (Diehard) всего из семи живых клеток, потомки которой существуют в течение 130 поколений, а затем исчезают.

«Conway's Game of Life»
Джон Конвей первоначально предположил, что никакая начальная комбинация не может привести к неограниченному размножению и предложил премию в $50 тому, кто докажет или опровергнет эту гипотезу.

«Conway's Game of Life»
Приз был получен группой из Массачусетского технологического института, придумавшей неподвижную повторяющуюся фигуру, которая периодически создавала движущиеся «планеры». Таким образом, количество живых клеток могло расти неограниченно. Затем были найдены движущиеся фигуры, оставляющие за собой «мусор» из других фигур.

«Conway's Game of Life»
И хотя игра состоит всего из двух простейших правил, она уже почти шестьдесят лет привлекает пристальное внимание учёных.

«Conway's Game of Life»
Многие закономерности, обнаруженные в этой игре, имеют свои аналогии в других, подчас совершенно «нематематических» дисциплинах:
биология: внешнее сходство с развитием популяций примитивных организмов;
физиология: рождение и смерть клеток Конвея аналогичны процессу возникновения и исчезновения нейронных импульсов, которые и формируют процесс мышления, а также аналогичны созданию импульсов в нервной системе многоклеточных организмов;

«Conway's Game of Life»
Многие закономерности, обнаруженные в этой игре, имеют свои аналогии в других, подчас совершенно «нематематических» дисциплинах:
астрономия: эволюции некоторых сложных колоний удивительным образом схематично повторяют этапы развития спиралевидных галактик;
физика твёрдого тела: теория автоматов, вообще, и игра «Жизнь», в частности, используются для анализа физических явлений переноса — диффузии, вязкости и теплопроводности;

«Conway's Game of Life»
Многие закономерности, обнаруженные в этой игре, имеют свои аналогии в других, подчас совершенно «нематематических» дисциплинах:
наномеханика: стационарные и пульсирующие колонии являются показательным примером простейших устройств, созданных на основе нанотехнологий;
социология: процессы доминации, вытеснения, поглощения, сосуществования, слияния и уничтожения популяций во многих аспектах схожи с явлениями, происходящими при взаимодействии больших, средних и малых социальных групп.

Контрольные вопросы
1. В каком году была появилось первое упоминание об игре «Жизнь» Джона Конвея?
1965
1930
1970
2001
2. Какую поверхность чаще всего используют для моделирования вселенной игры «Жизнь»?
Тор
Цилиндр
Эллипсоид
Шар
3. Рядом с живой клеткой находятся две живые соседки. Что произойдёт с этой клеткой на следующем шаге игры?
клетка погибнет
клетка продолжит жить
вокруг этой клетки оживут ещё две