История возникновения геометрии как науки

Геометрия
возникла очень давно, это одна из самых древних наук.

Геометрия (греческое, от ge — земля и metrein — измерять) — наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела.

Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии. Однако современная геометрия во многих своих дисциплинах выходит далеко за пределы этого определения.

Важную роль играли и эстетические потребности людей: желание украсить свои жилища

свою одежду

рисовать картины окружающей жизни

За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания

которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов

правил нахождения площадей фигур, объемов тел, построение прямых углов

Основные периоды развития
Период зарождения геометрии как математической науки.
- Период становления геометрии как самостоятельной математической науки.
- Период развития аналитической геометрии.
- Период формирования геометрии Лобачевского.

Классификация разделов геометрии
В соответствии с классификацией Феликса Клейна , в классической геометрии можно выделить следующие основные разделы.
Евклидова геометрия
Проективная геометрия
Афинная геометрия
Начертательная геометрия
Многомерная геометрия
Неевклидова геометрия

Зарождение геометрии как математической науки - протекало в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э.

Геометрия -
была перенесена в Грецию из Египта в 7 в. до н. э. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве

Этот процесс привёл, наконец, к качественному скачку. Геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались.

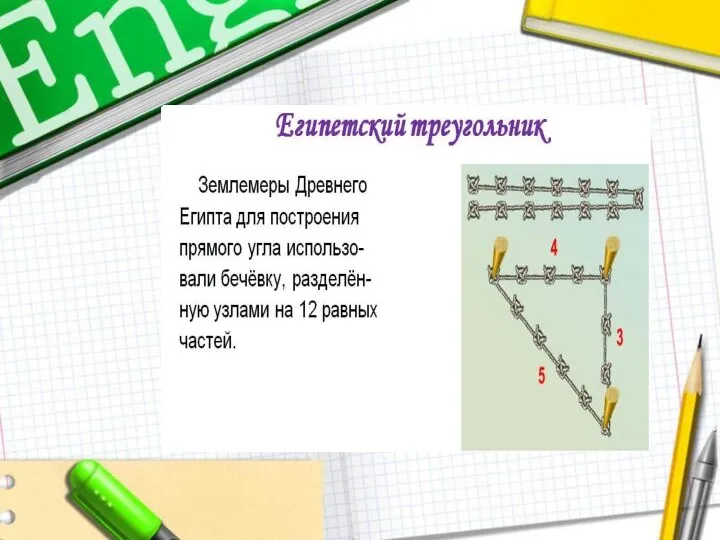
Имеются вполне достоверные сведения о значительном развитии геометрических знаний в Египте более чем за две тысячи лет до нашей эры. Узкая плодородная полоса земли между пустыней и рекой Нилом ежегодно подвергалась затоплению, и каждый раз разлив смывал границы участков, принадлежавших отдельным лицам. После спада воды требовалось с возможно большей точностью восстановить эти границы, ибо каждый из участков ценился весьма высоко.

Египетские пирамиды - одно из семи чудес света.

К задачам, которые решали алгебраическим и арифметическим методом, относятся и многие задания на определение длин, площадей при делении земельных участков, объемов земляных выемок, хозяйственных построек.

В дошедших до нас вавилонских табличках имеются задачи абстрактного характера и внешне кажущиеся не связанными с практическими нуждами. Но это не так: они возникли в результате теоретической обработки условий, первоначально порожденных потребностями практики при межевании земель, возведении стен и насыпей, при строительстве каналов, плотин, оборонительных сооружений и пр. Сохранилось немало планов земельных угодий, разделенных на участки прямоугольной, трапецеидальной или треугольной форм. Но соответствующие геометрические фигуры воспринимались ими как абстрактные, так прямоугольник они называли "то, что имеет длину и ширину", трапецию - "лбом быка", сегмент - "полем полумесяца", параллельные прямые - "двойными прямыми".

Жителям Вавилона пришлось труднее, чем жителям Египта. Так как их государство находилось между двумя реками: Евфрат и Тигр, которые разливались очень бурно, то для защиты населения и земель от наводнений они строили дамбы, обносили поля и селения насыпями. А для строительства всяких больших сооружений нужны знания.

Вавилонские ученые изучали свойства окружности. Учились измерять длину окружности. Вот как они поступали: чертили окружность и два квадрата: один – так, чтобы его углы упирались в окружность изнутри, второй квадрат побольше рисовали так, чтобы окружность помещалась в нем. Потом измеряли длину сторон большого и меньшего квадратов (это легко сделать линейкой). Получившиеся числа складывали и делили пополам ,и это число считалось длиной окружности.

К задачам, которые решали вавилоняне, относятся и многие задания на определение длин площадей при делении земельных участков, объемов земляных выемок, хозяйственных построек. Жители Вавилона внесли огромный вклад в последующее развитие геометрии.

Свой путь, как наука, геометрия начала в Греции. Греки были удивительным и умным народом, у которых многому учатся даже сейчас, спустя тысячи лет.
Они задавались такими вопросами: почему в равнобедренном треугольнике углы при основании равны, почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах.
Пожалуй, никто в истории человечества не сделал столько же открытий, сколько сделали греки.
Геометрия в Греции

Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили.

Историки науки выделяют три периода ее развития в соответствии с характером знаний:
1 - Накопление отдельных математических фактов и проблем (6 - 5B.B. до н.э.).
2 - Систематизация полученных знаний (4 - 3 в.в. до н.э.).
3 - Период вычислительной математики (3в. до н.э. - 6 в.).
Необыкновенный расцвет науки и культуры был тесно связан с общим подъемом греческого производства 6 - 4 в.в. до н.э., жизненными потребностями людей.

Фалес Милетский
был одним из великих греческих учёных,(640 - 548 г.г. до н.э.). Он принадлежал к числу «семи мудрецов» античного мира и считался основателем ионийской школы. Фалес посетил Египет, там он познакомился с астрономией и геометрией. Легенда рассказывает о том, что Фалес привел в изумление египетского царя Амазиса, измерив высоту одной из пирамид по величине отбрасываемой ею тени.

В геометрии ему приписывают ряд утверждений: Диаметр делит окружность (круг) пополам;
Теорему о равенстве вертикальных углов;
3). Углы при основании равнобедренного треугольника равны;
4). Второй признак равенства треугольников;
5). Теорему о том, что угол, вписанный в полукруг, прямой. Фалес мыслил углы не как величины, а как фигуры, имеющие некоторую форму.

Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия.

Пифагор Самосский (570 – 500 . до н. э.)
— древнегреческий философ и математик. Родился на острове Самос в Эгейском море, в семье купца Мнесарха. Путешествуя с отцом, будто бы в возрасте 18 – 20 лет, они посетили старого тогда уже Фалеса, который и пробудил интерес юноши к математике и астрономии. Он посоветовал ему поехать для основательного образования в Египет. Пифагор последовал совету. Затем был Вавилон и Индия.

По возвращении на Самос, Пифагор основал свою школу. В городе Кротоне им был основан знаменитый пифагорейский союз, бывший одновременно научной школой, политическим и религиозным сообществом, в котором Пифагор почитался чуть ли не божеством.

Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом».
Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей.

ВЕЛИКАЯ ТЕОРЕМА ПИФАГОРА
« Квадрат гипотенузы равен сумме квадратов катетов» - так гласит великая теорема Пифагора.
Об этом было известно далеко до Пифагора в Древнем Вавилоне ( видимо они вычислили это с помощью расчётов) , но доказал теорему первым Пифагор. Его доказательство не сохранилось.
Зато сейчас существует более 400 доказательств этой теоремы. Возможно, среди них есть и пифагорово доказательство

Известны упоминания систематические изложения геометрии, среди которых данное в 5 в. до н. э. Гиппократом Хиосским. Сохранились же и сыграли в дальнейшем решающую роль появившиеся около 300 до н. э. "Начала" Евклида. Упадок античного общества привёл к сравнительному застою в развитии геометрии, однако она продолжала развиваться в Индии, в Средней Азии, в странах арабского Востока.

Евклид( ок.365 - ок. 300 г. до н. э.)
жил в Александрии в эпоху, когда там образовался наиболее крупный центр греческой научной мысли. Опираясь на труды своих предшественников , среди которых были Фалес и Пифагор, Демокрит и Гиппократ, Архит, Теэтет, Евклид создал «Начала». Его «Начала» состояли из 13 книг: I –VI книги посвящены планиметрии; VII – X учению о числе; XI – XIII – стереометрии.

Составитель «Начал» — это прозвище. Оно сделалось как бы собственным именем, под которым все позднейшие греческие математики разумели Евклида, а его «Начала» сделались учебником, по которому в течение двух тысячелетий учились геометрии юноши и взрослые. До XIX в. в школах всего мира геометрия преподавалась по «Началам» Евклида. Изложение и методы доказательства многих теорем в современных учебниках те же, что в « Началах».

Труды Евклида

Для геометрии эпохи эллинизма характерен интерес к построению логически завершенных теорий . Наиболее ярко эта тенденция отразилась в творчестве Евклида Александрийского (III в. до н.э.).
В III в. до н.э. древнегреческий ученый Евклид написал книгу под названием "Начала". В ней он подытожил накопленные к тому времени геометрические знания и попытался дать законченное аксиоматическое изложение этой науки.

Написана она была настолько хорошо, что в течение 2000 лет преподавание геометрии велось либо по переводам, либо по незначительным переработкам книги Евклида.
Евклиду приписывается несколько теорем и новых доказательств, но их значимость не может быть сравнима с достижениями великих греческих геометров: Фалеса и Пифагора (VI в. до н.э.), Евдокса и Теэтета (IV в. до н.э.). Величайшая заслуга Евклида состоит в том, что он подвел итог

Он с величайшим искусством расположил материал по 13 книгам так, чтобы трудности не возникали преждевременно. Главная особенность "Начал" состоит в том, что они построены по единой логической схеме, и все содержащиеся в них теории строго обоснованы по принципу построения научных дисциплин, который намечался еще у Аристотеля.

ТРУДЫ АРХИМЕДА
Архимеду принадлежит формула для определения площади треугольника через три его стороны (неправильно именуемая формулой Герона). Архимед дал (не вполне исчерпывающую) теорию полуправильных выпуклых многогранников (архимедовы тела).

Особое значение имеет «аксиома Архимеда»: из неравных отрезков меньший, будучи повторен достаточное число раз, превзойдет больший. Эта аксиома определяет т. н. архимедовскую упорядоченность, которая играет важную роль в современной математике. Архимед построил счисление, позволяющее записывать и называть весьма большие числа. Он с большой точностью вычислил значение числа и указал пределы погрешности.

ТРУДЫ МЕНЕЛАЯ
Менелаем были написаны два сочинения: "О вычислении хорд", в 6 книгах, и "Сферика", в 3 книгах. Из них первое совсем не дошло до нас.

Из числа многих предложений, для нас впервые встречающихся в этом сочинении, самым замечательным считается обыкновенно теорема Менелая, которая прежде называлась правилом шести количеств (regula sex quantitatum). Содержание ее состоит в следующем. Если все стороны треугольника пересечь прямой, то произведение их трех отрезков, из числа не имеющих общих концов, равно произведению таких же трех остальных отрезков.

ТРУДЫ АПОЛЛОНА
АПОЛЛОНИЙ ПЕРГСКИЙ (ок. 260 — 170 до н. э.), древнегреческий математика и астроном, ученик Евклида. В основном труде «Конические сечения» (8 книг) дал полное изложение их теории.

Для объяснения видимого движения планет построил теорию эпициклов. Идеи Аполлона Пергского оказали большое влияние на развитие естествознания нового времени. Гипербола является коническим сечением. Она может быть получена, если секущая плоскость пересекает обе полости конической поверхности, не проходя через вершину.

Третий период
Аналитическая геометрия изучает фигуры и преобразования, задаваемые алгебраическими уравнениями в прямоугольных координатах, используя при этом методы алгебры. Дифференциальная геометрия, возникшая в 18 в. в результате работ Л. Эйлера, геометрия Монжа и др., исследует уже любые достаточно гладкие кривые линии и поверхности, их семейства (т. е. их непрерывные совокупности) и преобразования. Её название связано в основном с её методом, исходящим из дифференциального исчисления.

Период развития аналитической геометрии
Аналитическая геометрия изучает фигуры и преобразования, задаваемые алгебраическими уравнениями в прямоугольных координатах, используя при этом методы алгебры. Дифференциальная геометрия, возникшая в 18 в. в результате работ Л. Эйлера, геометрия Монжа и др., исследует уже любые достаточно гладкие кривые линии и поверхности, их семейства (т. е. их непрерывные совокупности) и преобразования.

К 1-й половине 17 в. относится зарождение проективной геометрии в работах Ж. Дезарга и Б. Паскаля. Она возникла из задач изображения тел на плоскости; её первый предмет составляют те свойства плоских фигур, которые сохраняются при проектировании с одной плоскости на другую из любой точки.

Само учение о геометрическом изображении (в прямой связи с задачами черчения) было ещё раньше (1799) развито и приведено в систему Монжем в виде начертательной геометрии. Во всех этих новых дисциплинах основы (аксиомы, исходные понятия) геометрии оставались неизменными, круг же изучаемых фигур и их свойств, а также применяемых методов расширялся

ТРУДЫ ЭЙЛЕРА

В элементарной геометрии Эйлер обнаружил несколько фактов, не замеченных Евклидом:
Три высоты треугольника пересекаются в одной точке (ортоцентре). В треугольнике ортоцентр, центр описанной окружности и центр тяжести лежат на одной прямой — «прямой Эйлера».
Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности (окружности Эйлера).
Число вершин (В), граней (Г) и рёбер (Р) у любого выпуклого многогранника связаны простой формулой: В + Г = Р + 2.

Второй том «Введения в анализ бесконечно малых» (1748) — это первый в мире учебник по аналитической геометрии и основам дифференциальной геометрии.
Термин аффинные преобразования впервые введён в этой книге вместе с теорией таких преобразований.
В 1760 году вышли фундаментальные «Исследования о кривизне поверхностей». Эйлер обнаружил, что в каждой точке гладкой поверхности имеются два нормальных сечения с минимальным и максимальным радиусами кривизны, и плоскости их взаимно перпендикулярны.
1771 год: опубликовано сочинение «О телах, поверхность которых можно развернуть на плоскость».

Четвёртый период
в развитии геометрия открывается построением Н. И. Лобачевским в 1826 новой, неевклидовой геометрия , называемой теперь Лобачевского геометрией. Лобачевский рассматривал свою геометрию как возможную теорию пространственных отношений; однако она оставалась гипотетической, пока не был выяснен (в 1868) её реальный смысл и тем самым было дано её полное обоснование.

Первый принцип заключается в том, что логически мыслима не одна евклидова геометрия , но и другие "геометрии".
Второй принцип - это принцип самого построения новых геометрических теорий путём видоизменения и обобщения основных положений евклидовой геометрии.

Третий принцип состоит в том, что истинность геометрической теории, в смысле соответствия реальным свойствам пространства, может быть проверена лишь физическим исследованием и не исключено, что такие исследования установят, в этом смысле, неточность евклидовой геометрии. Современная физика подтвердила это. Однако от этого не теряется математическая точность евклидовой геометрии, т.к. она определяется логической состоятельностью (непротиворечивостью) этой геометрии.

Никола́й Ива́нович Лобаче́вский
(20 ноября (1 декабря) 1792, Нижний Новгород — 12 (24) февраля 1856, Казань), великий русский математик, создатель геометрии Лобачевского, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии».

Первые попытки Лобачевского доказать пятый постулат относятся к 1823 году. К 1826 году он пришел к убеждению в том, что V постулат не зависит от остальных аксиом геометрии Евклида и 11(23) февраля 1826 года сделал на заседании факультета казанского университета доклад «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных», в котором были изложены начала открытой им «воображаемой геометрии», как он называл систему, позднее получившую название неевклидовой геометрии. Доклад 1826г. вошел в состав первой публикации Лобачевского по неевклидовой геометрии.

Неевклидова геометрия
Нельзя сказать, что неевклидова геометрия единственно правильная. На данный момент к ней нет никаких претензий. Но, может быть, через много лет она устареет. Так или иначе, но наука никогда не будет стоять на месте.
Геометрия Лобачевского не единственная, существуют и другие, например, геометрия Римана:
Геометрия Римана - многомерное обобщение геометрии на поверхности, представляющее собой теорию римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка сравнительно с размерами области). Геометрия Римана получила своё название по имени Б. Римана, который заложил её основы в 1854.

Статьи «О началах геометрии», напечатанной в журнале Казанского университета «Казанский вестник» в 1829-1820гг. дальнейшему развитию и приложениям открытой им геометрии были посвящены мемуары «Воображаемая геометрия», «Применение воображаемой геометрии к некоторым интегралам» и «Новые начала геометрии с полной теорией параллельных», опубликованные в «Ученых записках» соответственно в 1835, 1836 и 1835-1838 гг. Переработанный текст «Воображаемой геометрии» появился во французском переводе в Берлине, там же в 1840г. вышли отдельной книгой на немецком языке «Геометрические исследования по теории параллельных линий» Лобачевского. Наконец, в 1855 и 1856 гг. он издал в Казани на русском и французском языках «Пангеометрию».

Высоко оценил «Геометрические исследования» Гаусс, который провел Лобачевского (1842) в члены-корреспонденты Геттингенского ученого общества, бывшего по существу Академией наук ганноверского королевства. Однако в печати с оценкой новой геометрической системы Гаусс не выступил. Высокая оценка Гауссом открытия Лобачевского была связана с тем, что Гаусс, еще с 90-х годов XVIII в. занимавшийся теорией параллельности линий ,пришел к тем же выводам, что и Лобачевский. Свои взгляды по этому вопросу Гаусс не публиковал, они сохранились только в его черновых записках и в немногих письмам к друзьям.

Независимо от Лобачевского и Гаусса к открытию неевклидовой геометрии пришел венгерский математик Янош Бояи (1802-1860), сын Ф. Бояи. Когда Я. Бояи пришел к тем же идеям, что Лобачевский и Гаусс, отец не понял его, однако предложил напечатать краткое изложение его открытия в виде приложения к своему руководству по математике, вышедшему в 1832г. Полное название труда Я. Бояи – «Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)» и его обычно коротко называют просто «Аппендикс». Открытие Я. Бояи не было признано при его жизни; Гаусс, которому Ф. Бояи послал "Аппендикс", понял его, но никак не способствовал признанию открытия Я. Бояи.

Наиболее полно изложена система Лобачевского в его «Новых началах с полной теорией параллельных» (1835-1838). Изложение геометрии у Лобачевского основывается на чисто топологических свойствах прикосновения и сечения, конгруэнтность тел и равенство отрезков определяются по существу с помощью движения. В позднейших работах Лобачевский ввел координаты и вычислил из геометрических соображений целый ряд новых определенных интегралов, которым он специально посвятил работу «Применение воображаемой геометрии к некоторым интегралам»

Классическая геометрия XIX века
XIX век принес с собой новый глубокий переворот и в содержании геометрии, и в ее методах, и в самых взглядах на ее сущность. Наиболее характерной чертой новой геометрии была ее алгебраизация. Но из самых корней алгебраического метода росли противоречия, имевшие двоякий источник.
Во-первых, сама алгебра не так уж сильна. Границы классической геометрии определялись теми вопросами, которые алгебраически сводятся к уравнениям 1-й и 2-й степени

Геометрия XX века
Подобно тому, как проективная геометрия создалась из разрозненных материалов, скоплявшихся с Дезарга в течение двух веков, так из многообразных отрывочных идей, рассеянных по всей истории геометрии, в XX в. складывается особая дисциплина — топология. К началу XX века относится зарождение векторно-моторного метода в начертательной геометрии, применяющегося в строительной механике, машиностроении. Этот метод разработан Б. Майором и Р. Мизесом, Б.Н. Горбуновым.Геометрическая сторона построенной Эйнштейном теории относительности, особенно оттененная Минковским, заключается в том, что мироздание, не в его статическом состоянии в определенный момент, а во всей его извечной динамике, Эйнштейн и Минковский рассматривают как многообразие, элемент которого определяется четырьмя координатами.