Квадратные неравенства

Определение
Неравенства вида
ax² + bx + c > 0 и ax² + bx + c < 0,
(ax² + bx + c ≥ 0; ax² + bx + c ≤ 0) где x – переменная, a, b и c некоторые числа и a ≠ 0, называют неравенствами второй степени с одной переменной или квадратными неравенствами

Способы решения
Метод ИНТЕРВАЛОВ
Графический способ

Метод ИНТЕРВАЛОВ
1) Найти корни соответствующего
квадратного уравнения ах²+вх+с = 0;
2) Корни уравнения нанести на числовую ось;
3) Разделить числовую ось на интервалы;
4) Определить знаки функции в каждом из интервалов;
5) Выбрать подходящие интервалы и записать ответ.

Например

Наносим на числовую прямую корни уравнения и определяем знаки
-6 1 х
5) Запишем ответ:
(-∞; -6]U[1; +∞)
+
+

Решить неравенства
1) х(х+7)≥0;
2) (х-1)(х+2)≤0;
3) х- х²+2<0;
4) -х²- 5х+6>0;
5) х(х+2)<15

Графический способ
1) Определить направление ветвей параболы, по знаку первого коэффициента квадратичной функции.
2) Найти корни соответствующего квадратного уравнения;
3) Построить эскиз графика и по нему определить промежутки, на которых квадратичная функция принимает положительные или отрицательные значения
4) Выбрать нужный промежуток и записать ответ

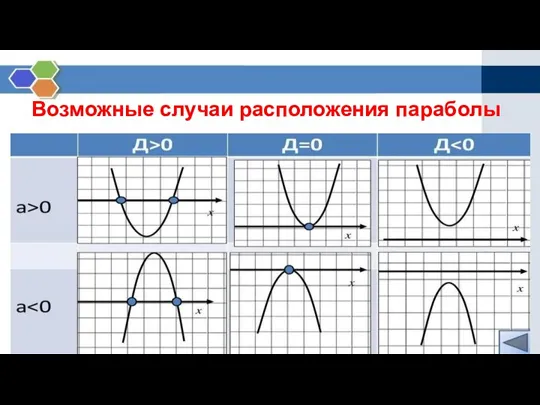
Возможные случаи расположения параболы

Например
Решить неравенство х²+5х-6≤0
Решение: 1). рассмотрим функцию
у = х²+5х-6,
это квадратичная функция, графиком является парабола, т.к. а =1, то ветви направлены вверх.

- 6
х
+
+
4). Запишем ответ:
(-∞; -6]U[1; +∞)

Решить неравенства
1) х²-3х<0;
2) х²- 4х>0;
3) х²+2х ≥ 0;
4) -2х²+х+1 ≤ 0