Приращение функции. Нахождение значения функции в точке

Нахождение значения функции в точке.
Найти значение функции f(x)= x2 + 2x в точке x0 = -3.
Решение: f(x0) = f(-3) = (-3)2+ 2∙(-3) = 9 - 6 = 3
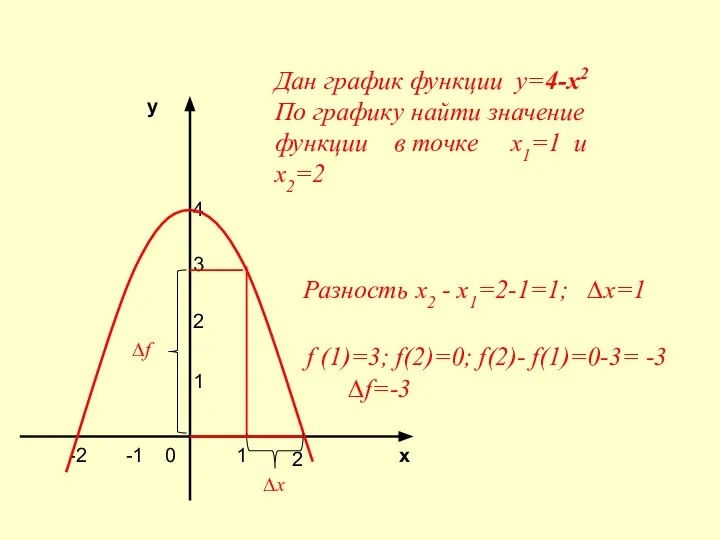
Ответ: f(-3) = 3

4
3
2
1
у
х
2
-2
-1
1
0
Дан график функции у=4-х2
По графику найти значение функции в точке х1=1 и х2=2
Разность х2 - х1=2-1=1; ∆x=1
f (1)=3; f(2)=0; f(2)- f(1)=0-3= -3
∆f=-3
∆x
∆f

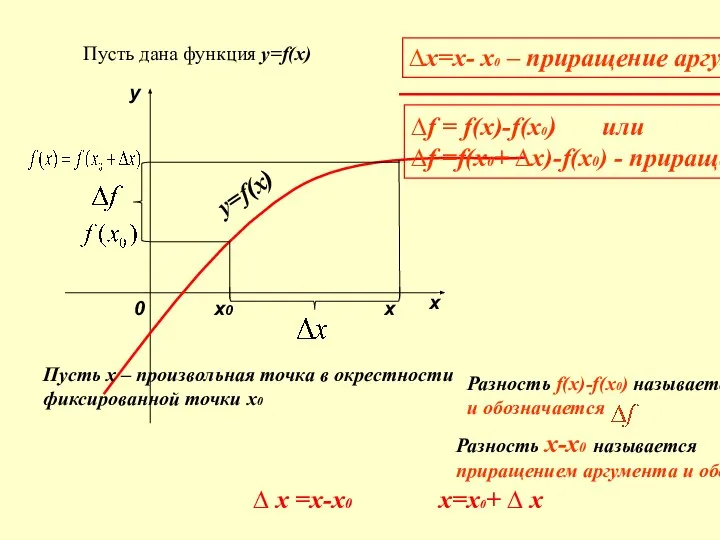
у=f(х)
Пусть дана функция у=f(х)
y
x
0
х
х0
Пусть х – произвольная точка в окрестности
фиксированной точки х0
Разность х-х0 называется
приращением аргумента и обозначается
Разность f(x)-f(x0) называется приращением функции
и обозначается
∆f = f(x)-f(x0) или
∆f =f(x0+ ∆x)-f(x0) - приращение функции
∆х=х- х0 – приращение аргумента
∆ x =x-x0 х=х0+ ∆ x

Определение.
Приращением аргумента функции называется величина, равная разности между конечным и начальным значением аргумента: ∆ x =x-x0
Определение.
Приращением функции называется величина, равная разности между конечным и начальным значением функции ∆f =f(x) - f(x0) = f(х0 + х)– f(x0).

Δ, δ (название: де́льта, греч. δέλτα) — 4-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 4. Происходит от Финикийской буквы — далет, название которой означало «дверь» или «вход в палатку». От буквы «дельта» произошли латинская буква D и кириллическая Д. Обозначение приращения функции (аргумента) буквой дельта впервые применил швейцарский математик и механик Иоганн Бернулли (1667-1748)

Пример 1
Найти приращение аргумента и приращение функции y=x2 при переходе от х0=1,2 к точке х=2,5
Решение: ∆ x= х-х0
∆ x=2,5-1,2=1,3,
∆f =f(x) - f(x0)
∆f=2,52-1,22=6,25-1,44= 4,81
Ответ: 1,3; 4,81

Пример 2:
Найти приращение аргумента и приращение функции в точке х0, если
Решение:

Найдите приращение функции f в точке х0, если
f(x) = 3x+1, x0 = 5, ∆x = 0, 01.
Решение: х=х0+∆x, х= 5+0,01=5,01
f(х0)=f(5)=3·5+1=16;
f (x)=f(5,01)= 3·5,01+1=16,03
Δf = f(x) - f(x0); Δf = 16,03-16=0,03
Ответ: 0,03

Найти приращение функции y=f(x) при переходе от точки х к точке х+∆x, если f(x)= х2 .
Решение: Δf = f(x) - f(x0)=f(х+ ∆x)-(x)
f(x)=x2
f(х+ ∆x) =(х+ ∆x)2=x2+2x∆x+∆x2
Δf= x2+2x∆x+∆x2 - x2=2x∆x+∆x2
Ответ: 2x∆x+∆x2