Метод Гаусса

Составим для нее расширенную матрицу, отделив столбец правых частей вертикальной чертой:
знак равенства.
правую часть уравнения;

Вспомним элементарные преобразования, не изменяющие решение системы.
Для расширенной матрицы системы Р допустимы:
Преобразования коэффициентов при неизвестных и правых частей системы удобно выполнять в матричной форме.
Метод Гаусса состоит в последовательном исключении неизвестных с помощью элементарных преобразований.
Вычисления проводятся в два этапа, называемых ПРЯМЫМ и ОБРАТНЫМ ХОДОМ.
ЗАМЕЧАНИЕ: рекомендуется нумеровать столбцы или проставлять под столбцами соответствующие неизвестные:

Прямой ход
Приведем расширенную матрицу системы Р к ступенчатому виду с помощью элементарных преобразований :
Возможны две
ситуации:

которое не имеет решений.
Решение закончено, обратный ход метода Гаусса не нужен.
система несовместна.
Какой ответ следует дать ?

и система уравнений совместна.
Выделим базисный минор и отбросим нулевые строки:

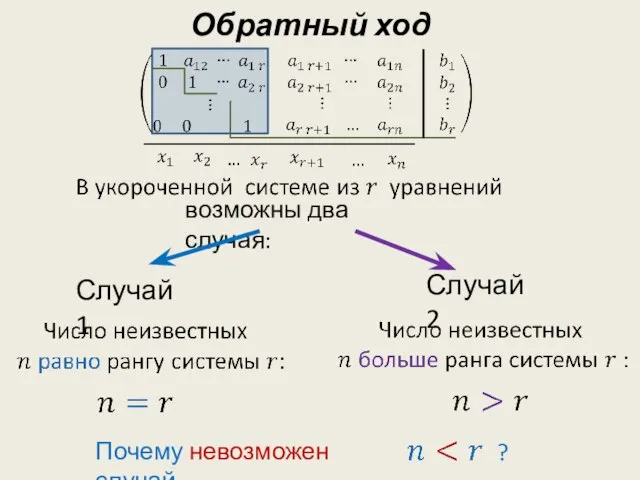
Обратный ход
возможны два случая:
Случай 1
Случай 2
Почему невозможен случай
?

Случай 1
то есть матрица системы стала треугольной :
Если вернуться к уравнениям, то получим
Решая последовательно уравнения системы снизу вверх, каждый раз будем иметь дело с уравнением, содержащим только одно неизвестное.
(называется определенной)

Случай 2
назовем их БАЗИСНЫМИ.
ВОПРОС: сколько свободных неизвестных?
БАЗИСНЫЕ
СВОБОДНЫЕ

Придадим свободным переменным любые значения и подставим их в уравнения:
Перейдем от матричной формы записи к уравнениям:
БАЗИСНЫЕ
СВОБОДНЫЕ
БАЗИСНЫЕ
СВОБОДНЫЕ

Выразим базисные переменные через свободные. Для этого перенесем в правую часть уравнений слагаемые со свободными переменными
(изменив знак на противоположный!!!):
Придавая свободным переменным другие значения, получим другие значения базисных. Система будет иметь БЕСКОНЕЧНОЕ МНОЖЕСТВО решений.
БАЗИСНЫЕ
СВОБОДНЫЕ
Вычислим базисные переменные(как в случае 1), решая последовательно уравнения системы снизу вверх.
(называется неопределенной)