Слайд 2I. СВЕДЕНИЕ К АЛГЕБРАИЧЕСКОМУ.

Слайд 3Пример:
Пусть .
Уравнение примет вид:
- не удовлетворяет условию
Ответ: .

Слайд 4II. ОДНОРОДНЫЕ И СВОДИМЫЕ К НИМ.

Слайд 5 Уравнение вида
называется однородным уравнением I степени.

Слайд 6 Пример:
Множество значений x, удовлетворяющих уравнению
, не является решением данного уравнения.

Поэтому можно обе части уравнения разделить на .
Получим:
Ответ: .
Слайд 7 Уравнение вида
называется однородным уравнением II степени.

Слайд 8Пример:
Решение:
Множество значений x, удовлетворяющих уравнению , не является решением данного уравнения.
Разделим обе

части уравнения на .
Получим:
Слайд 9Пусть .
Уравнение примет вид:
Ответ:

Слайд 10III. ЕСЛИ В УРАВНЕНИИ СОДЕРЖИТСЯ ПРОИЗВЕДЕНИЕ ФУНКЦИЙ SIN(АX)SIN(BX), SIN(AX)COS(BX), COS(AX)COS(BX), ТО ТАКИЕ

УРАВНЕНИЯ РЕШАЮТСЯ ПРЕОБРАЗОВАНИЕМ ПРОИЗВЕДЕНИЯ В СУММУ (РАЗНОСТЬ) И НАОБОРОТ.
Слайд 15Если в уравнении содержатся чётные степени sinx и cosx, то понижают степень

уравнения с применением понижающих формул:
Слайд 19VI. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА.

Слайд 20Пример
Решение:
Разделим обе части уравнения на
Получаем:
Ответ:

Слайд 21VII. ПРИМЕНЕНИЕ УНИВЕРСАЛЬНОЙ ПОДСТАНОВКИ.

Слайд 23Пример
Решение:
Пусть: . Уравнение примет вид . О.Д.З. .
не удовлетворяет условию
Ответ: ;

.
Слайд 24Пример 2:
Решение:
Проверка:
Ответ: ; .

Слайд 25VIII. ВВЕДЕНИЕ НОВОГО ПЕРЕМЕННОГО.

Слайд 26! Если в уравнении содержится сумма или разность sinx и cosx и

их произведения, то уравнение решается введением нового переменного:
Слайд 27Пример:
Пусть:
(Решите самостоятельно)
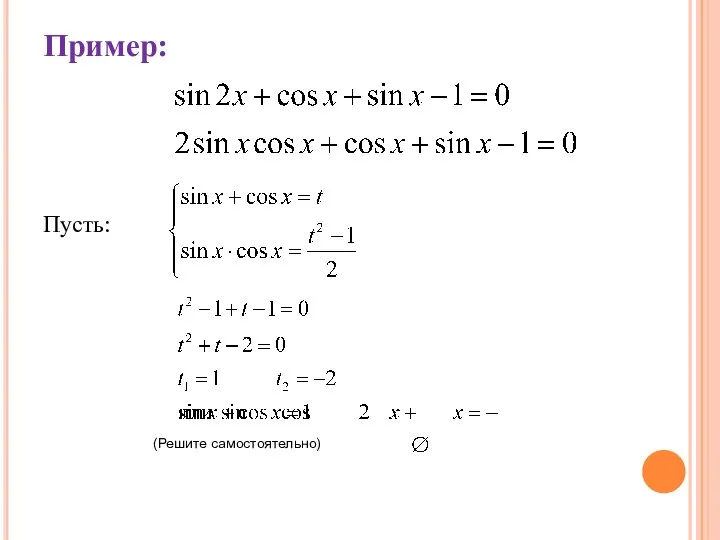
Слайд 28IX. ИСПОЛЬЗОВАНИЕ ПОНЯТИЯ ОГРАНИЧЕННОСТИ (МИНИМАКС).











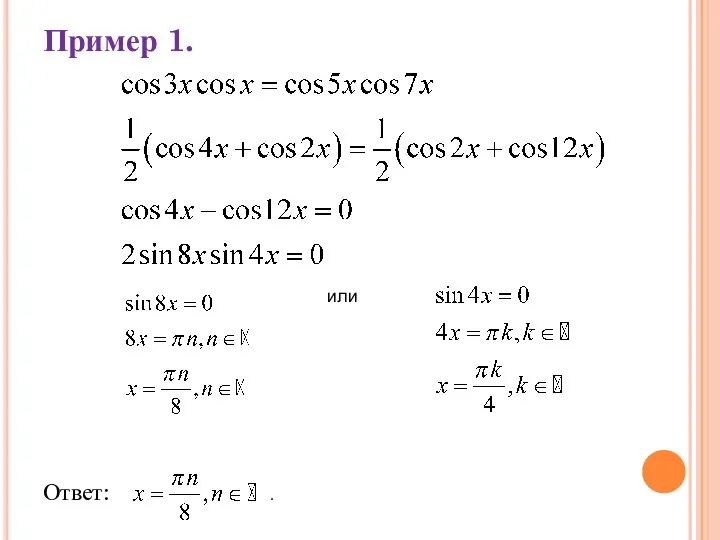



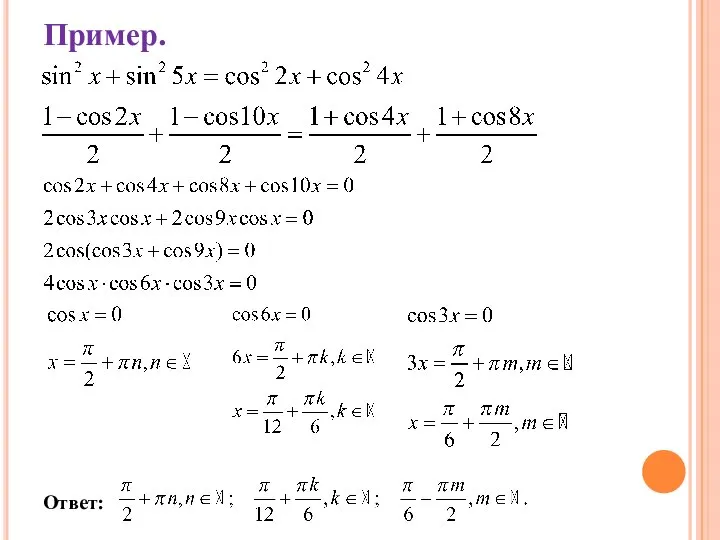









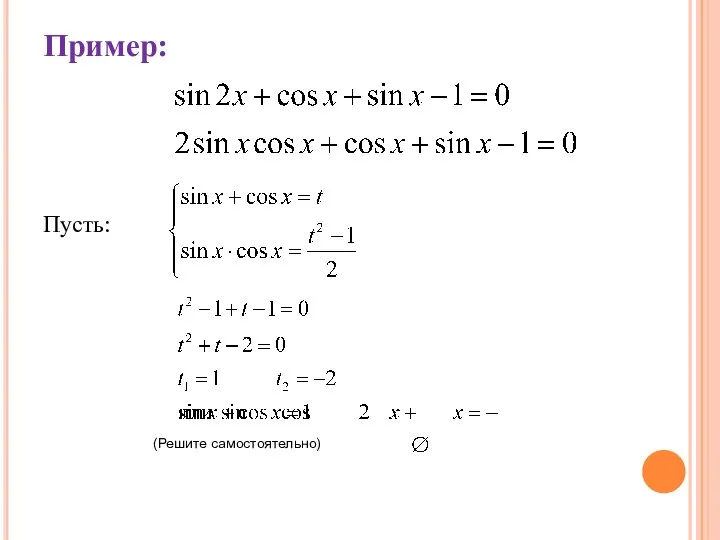


 Приемы устных вычислений в пределах 100. 3 класс
Приемы устных вычислений в пределах 100. 3 класс Презентация на тему Площади и объемы
Презентация на тему Площади и объемы  Симметрия в искусстве
Симметрия в искусстве Векторы. Свойства равных векторов
Векторы. Свойства равных векторов Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач
Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач Решение тригонометрических уравнений. Уравнения, сводящиеся к алгебраическим
Решение тригонометрических уравнений. Уравнения, сводящиеся к алгебраическим Примеры арифметических операций
Примеры арифметических операций Интегривование тригонометрических функций
Интегривование тригонометрических функций Шар. Сфера
Шар. Сфера Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, сводящиеся к квадратным Вписанный угол
Вписанный угол График функции y = kf (x)
График функции y = kf (x) Презентация на тему Знаки больше, меньше, равно (1 класс)
Презентация на тему Знаки больше, меньше, равно (1 класс)  Задание на треугольники
Задание на треугольники Сложение вида
Сложение вида Деление дробей
Деление дробей Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл 08.09
08.09 Справочный материал. 9 класс
Справочный материал. 9 класс Решение тестовых задач. Готовимся к ЕГЭ
Решение тестовых задач. Готовимся к ЕГЭ Преобразование тригонометрического выражения
Преобразование тригонометрического выражения Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Синус, косинус, тангенс
Синус, косинус, тангенс Уравнение древности. Франсуа Виет
Уравнение древности. Франсуа Виет Графики кусочных функций
Графики кусочных функций Решение задач
Решение задач Вычисление площадей
Вычисление площадей Единицы, десятки
Единицы, десятки