Содержание
- 2. Авторский сайт: vasmirnov.ru
- 3. Учебник геометрии Л.С. Атанасяна и др.
- 4. Учебник геометрии А.В. Погорелова
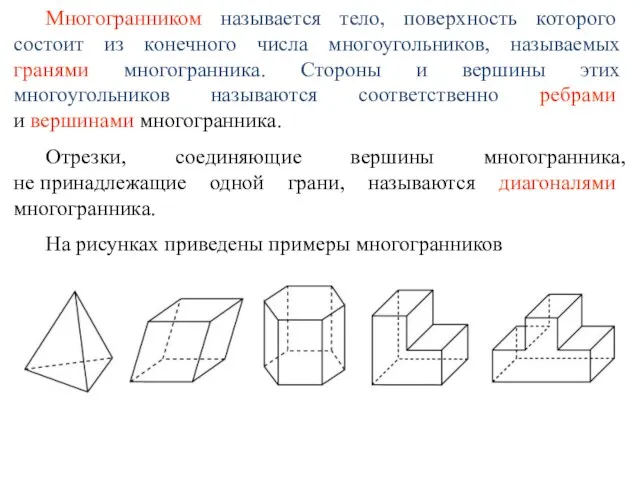
- 6. Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников, называемых гранями многогранника. Стороны и вершины
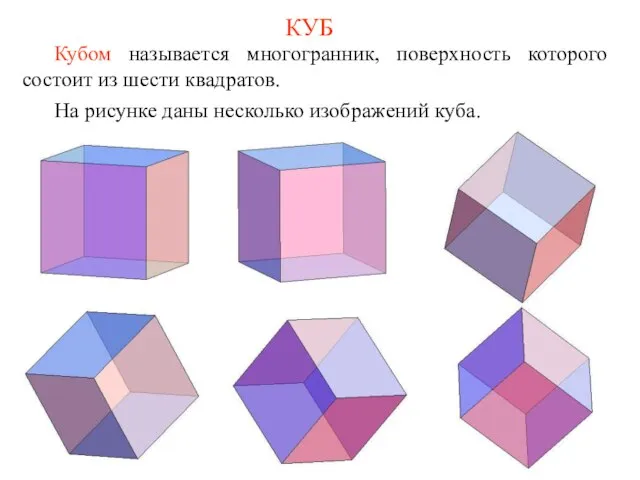
- 7. КУБ Кубом называется многогранник, поверхность которого состоит из шести квадратов. На рисунке даны несколько изображений куба.
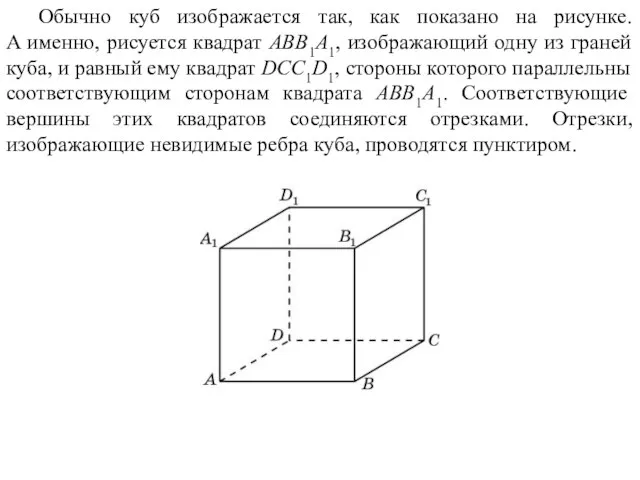
- 8. Обычно куб изображается так, как показано на рисунке. А именно, рисуется квадрат ABB1A1, изображающий одну из
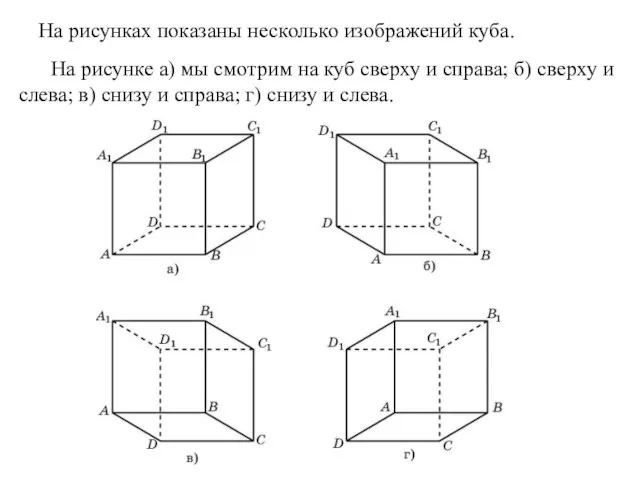
- 9. На рисунках показаны несколько изображений куба. На рисунке а) мы смотрим на куб сверху и справа;
- 10. Упражнения Сколько вершин (В), рёбер (Р) и граней (Г) имеет куб? Ответ: В = 8, Р
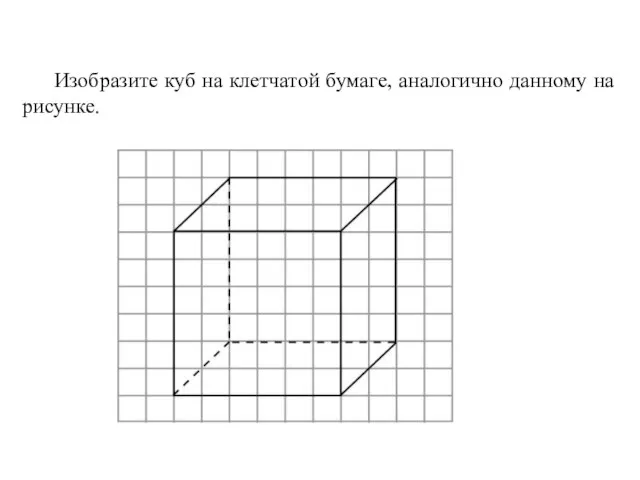
- 11. Изобразите куб на клетчатой бумаге, аналогично данному на рисунке.
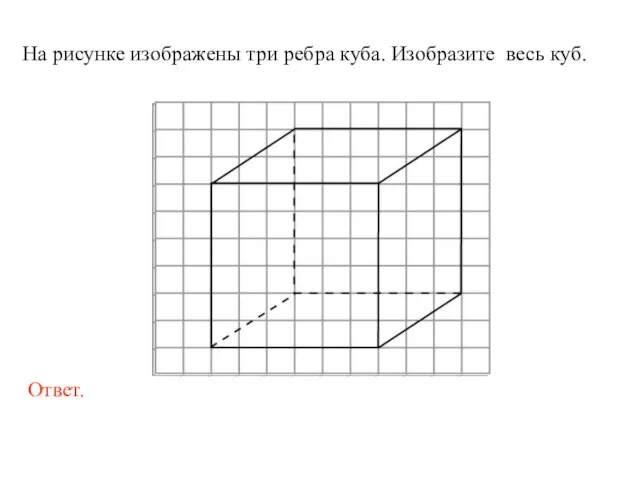
- 12. На рисунке изображены три ребра куба. Изобразите весь куб.
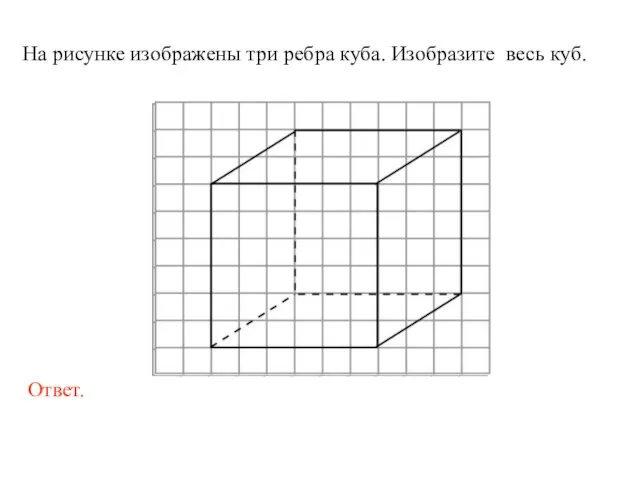
- 13. На рисунке изображены три ребра куба. Изобразите весь куб.
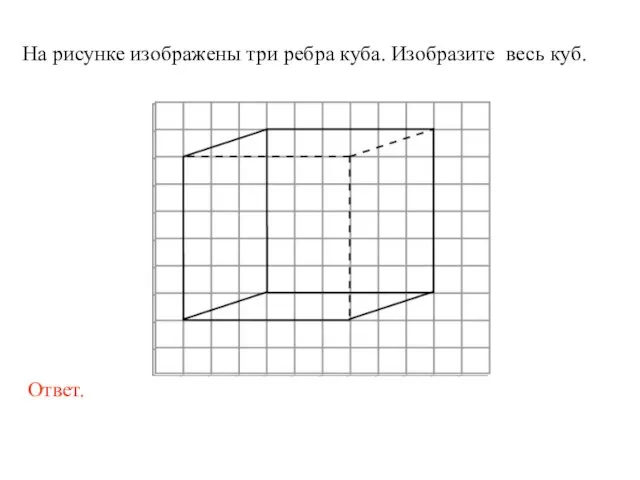
- 14. На рисунке изображены три ребра куба. Изобразите весь куб.
- 15. На рисунке изображены три ребра куба. Изобразите весь куб.
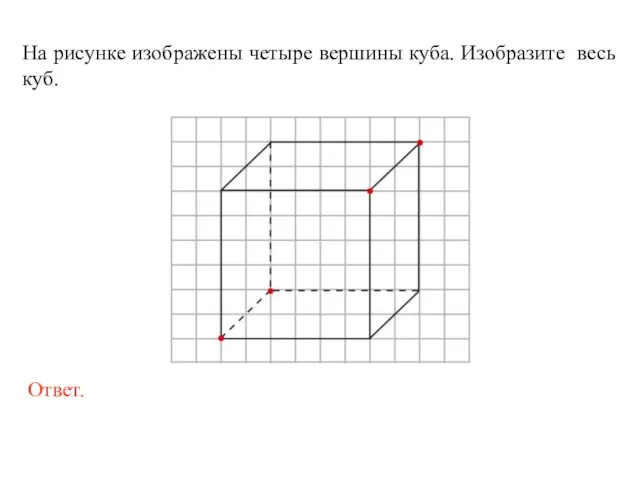
- 16. На рисунке изображены четыре вершины куба. Изобразите весь куб.
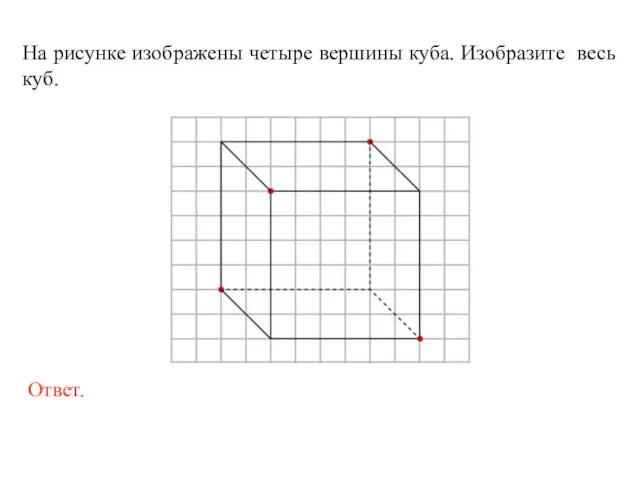
- 17. На рисунке изображены четыре вершины куба. Изобразите весь куб.
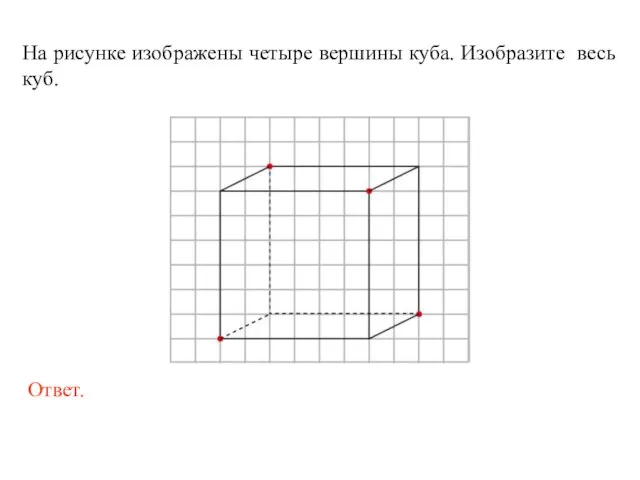
- 18. На рисунке изображены четыре вершины куба. Изобразите весь куб.
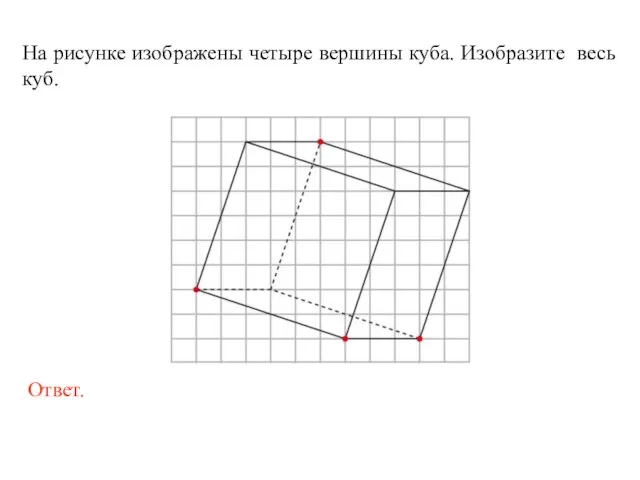
- 19. На рисунке изображены четыре вершины куба. Изобразите весь куб.
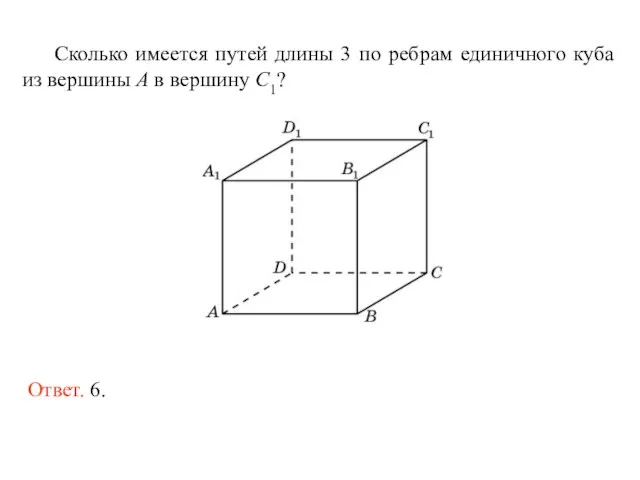
- 20. Сколько имеется путей длины 3 по ребрам единичного куба из вершины A в вершину C1? Ответ.
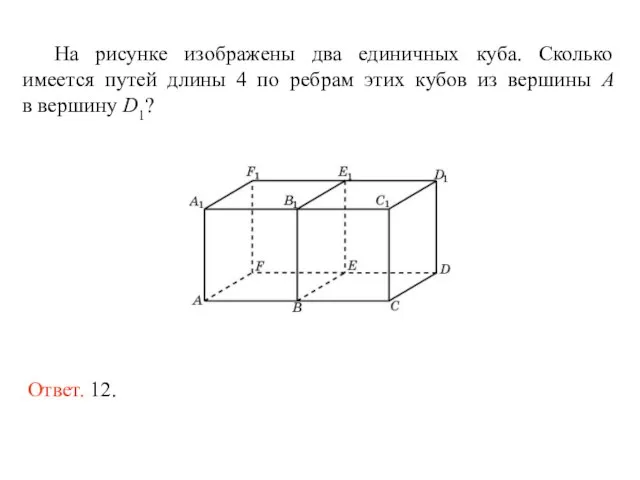
- 21. На рисунке изображены два единичных куба. Сколько имеется путей длины 4 по ребрам этих кубов из
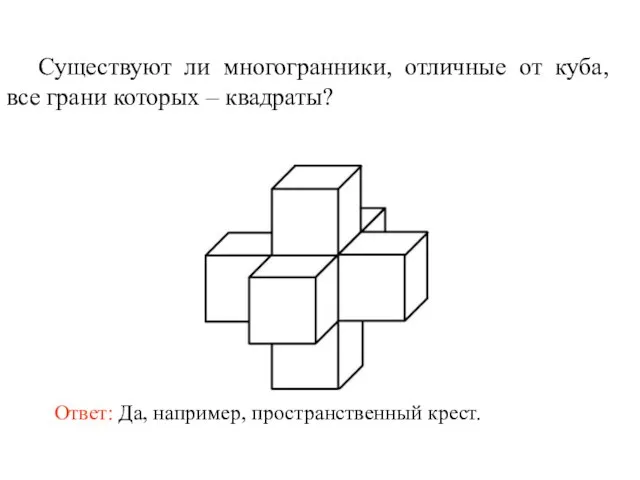
- 22. Существуют ли многогранники, отличные от куба, все грани которых – квадраты?
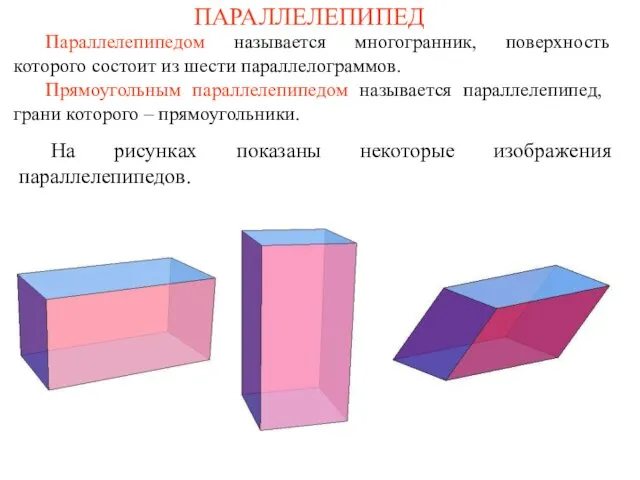
- 23. На рисунках показаны некоторые изображения параллелепипедов. ПАРАЛЛЕЛЕПИПЕД Параллелепипедом называется многогранник, поверхность которого состоит из шести параллелограммов.
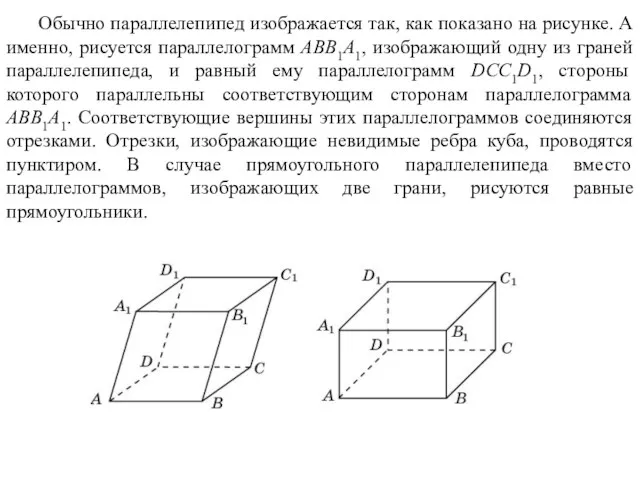
- 24. Обычно параллелепипед изображается так, как показано на рисунке. А именно, рисуется параллелограмм ABB1A1, изображающий одну из
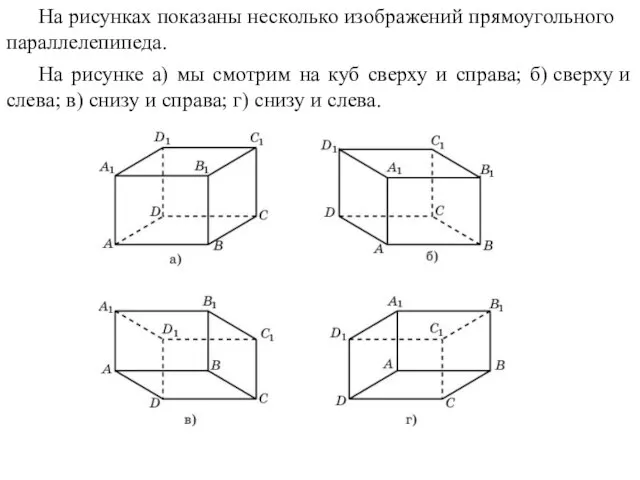
- 25. На рисунках показаны несколько изображений прямоугольного параллелепипеда. На рисунке а) мы смотрим на куб сверху и
- 26. Упражнения Укажите номера рисунков, на которых изображен параллелепипед? 1 2 3 4 5 6 Ответ: 1,
- 27. Сколько вершин (В), рёбер (Р) и граней (Г) имеет параллелепипед? Ответ: В = 8, Р =
- 28. Изобразите прямоугольный параллелепипед на клетчатой бумаге, аналогично данному на рисунке.
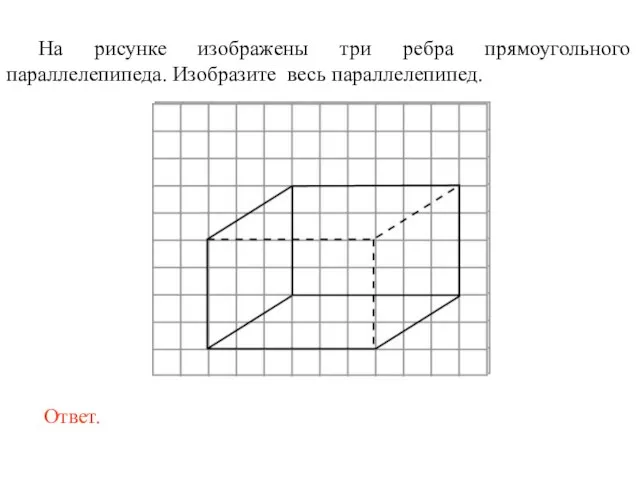
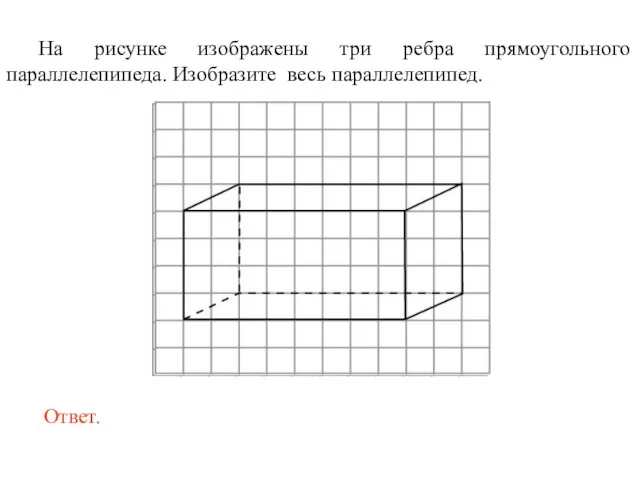
- 29. На рисунке изображены три ребра прямоугольного параллелепипеда. Изобразите весь параллелепипед.
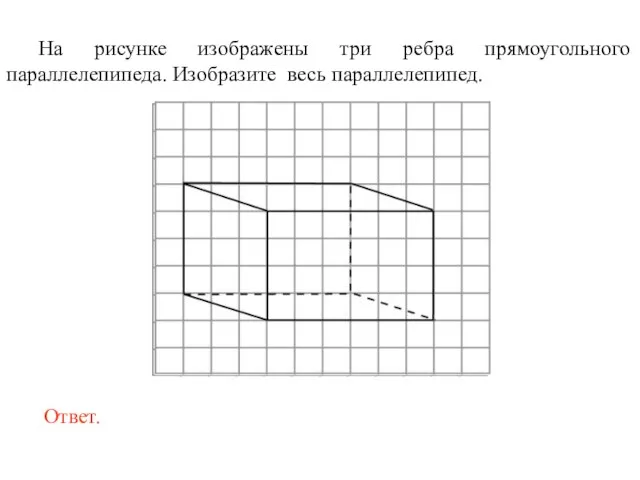
- 30. На рисунке изображены три ребра прямоугольного параллелепипеда. Изобразите весь параллелепипед.
- 31. На рисунке изображены три ребра прямоугольного параллелепипеда. Изобразите весь параллелепипед.
- 32. На рисунке изображены три ребра прямоугольного параллелепипеда. Изобразите весь параллелепипед.
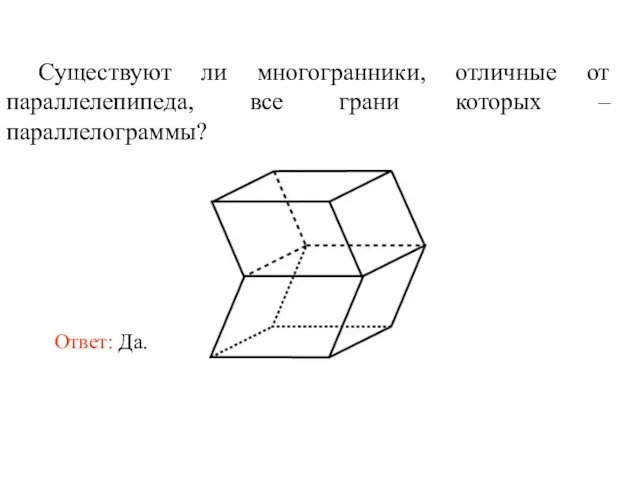
- 33. Существуют ли многогранники, отличные от параллелепипеда, все грани которых – параллелограммы?
- 34. Определение призмы в учебнике Л.С. Атанасяна и др.
- 35. Определение призмы в нашем учебнике Призмой называется многогранник, поверхность которого состоит из двух равных многоугольников, называемых
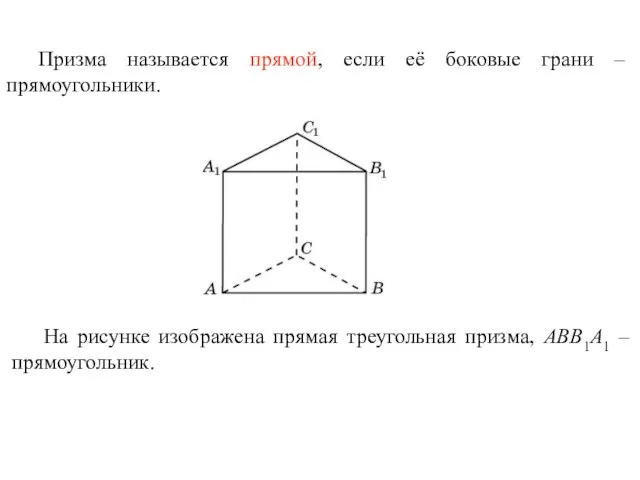
- 36. Призма называется прямой, если её боковые грани – прямоугольники. На рисунке изображена прямая треугольная призма, ABB1A1
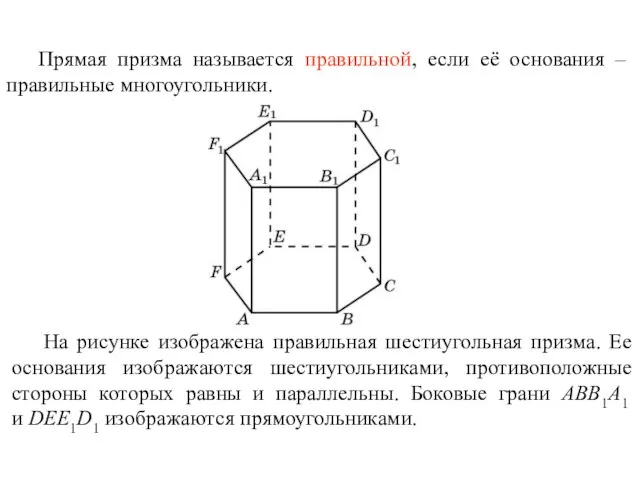
- 37. Прямая призма называется правильной, если её основания – правильные многоугольники. На рисунке изображена правильная шестиугольная призма.
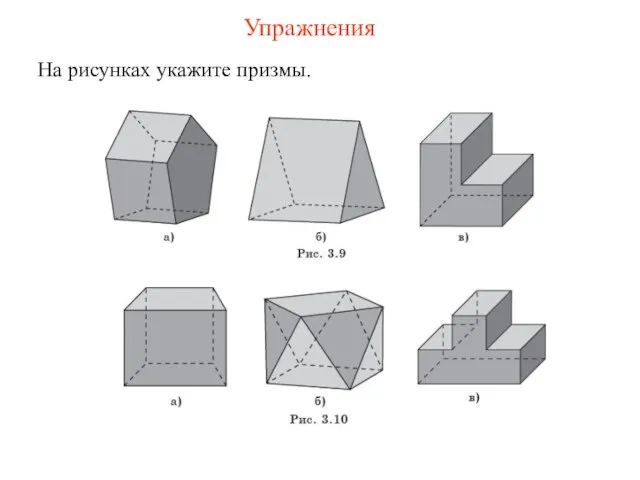
- 38. На рисунках укажите призмы. Упражнения
- 39. Сколько вершин (В), рёбер (Р) и граней (Г) имеет n‑угольная призма? Ответ: В = 2n, Р
- 40. Существует ли призма, которая имеет: Ответ: Нет. а) 4 ребра? Ответ: Нет. Ответ: Да. Ответ: Да.
- 41. Какой многоугольник лежит в основании призмы, которая имеет: Ответ: Шестиугольник. а) 18 рёбер? б) 24 вершины?
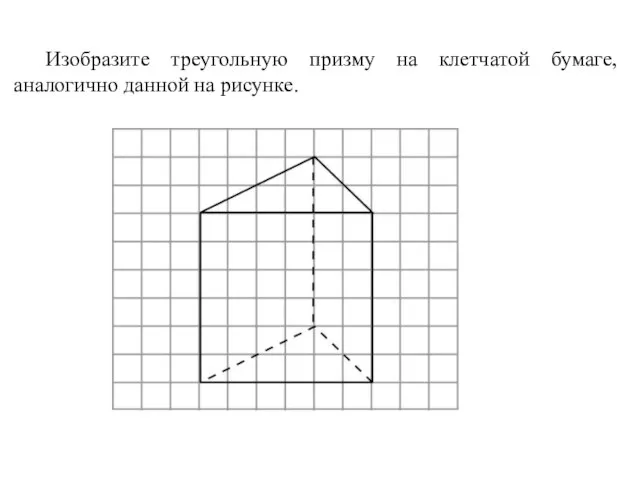
- 42. Изобразите треугольную призму на клетчатой бумаге, аналогично данной на рисунке.
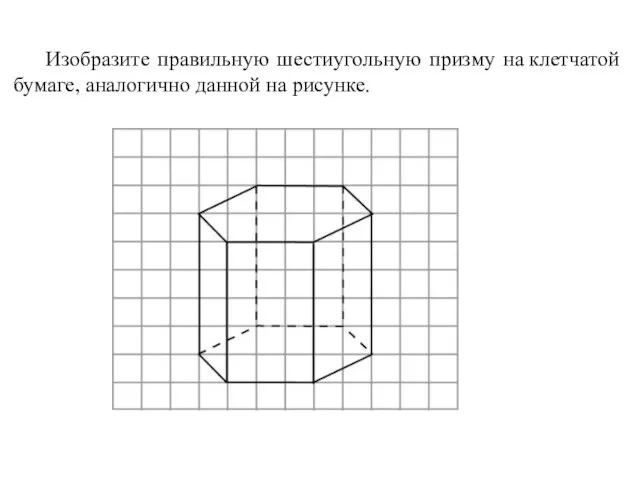
- 43. Изобразите правильную шестиугольную призму на клетчатой бумаге, аналогично данной на рисунке.
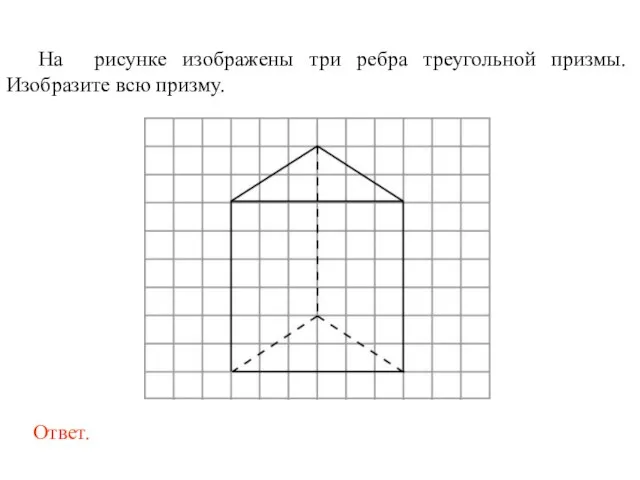
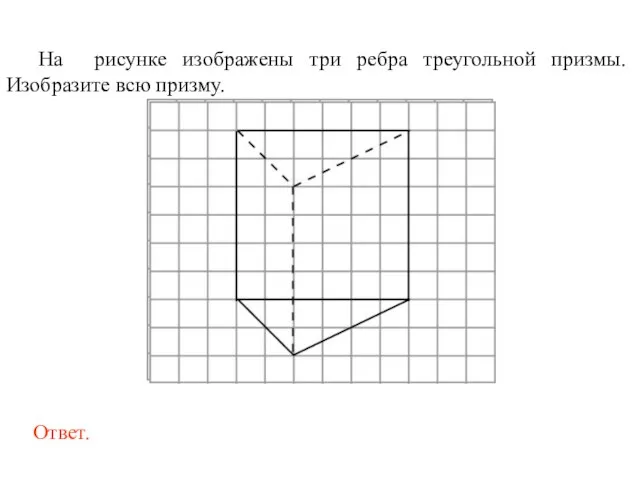
- 44. На рисунке изображены три ребра треугольной призмы. Изобразите всю призму.
- 45. На рисунке изображены три ребра треугольной призмы. Изобразите всю призму.
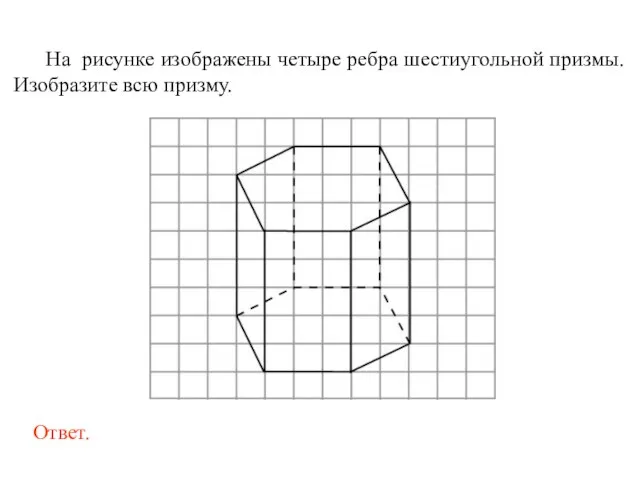
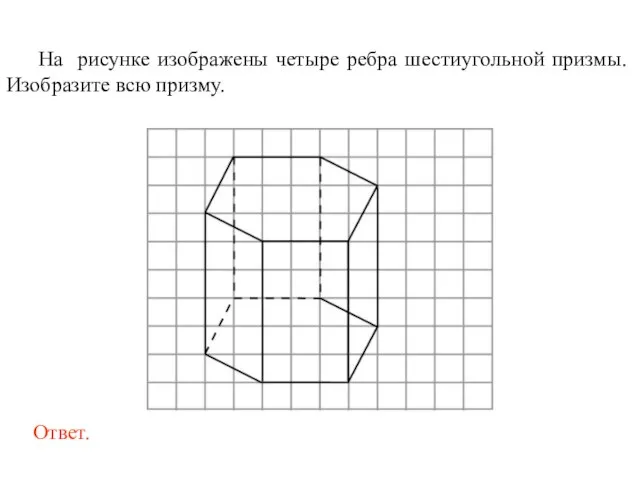
- 46. На рисунке изображены четыре ребра шестиугольной призмы. Изобразите всю призму.
- 47. На рисунке изображены четыре ребра шестиугольной призмы. Изобразите всю призму.
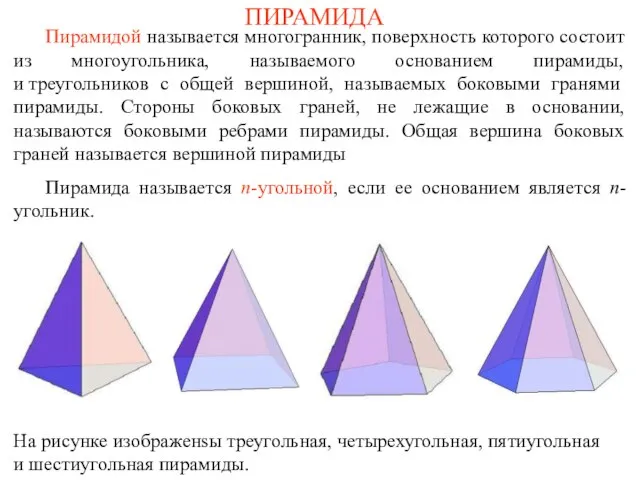
- 48. ПИРАМИДА Пирамидой называется многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников с общей
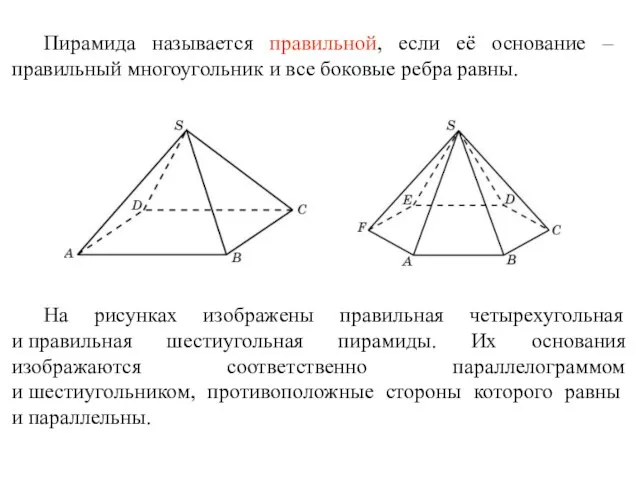
- 49. Пирамида называется правильной, если её основание – правильный многоугольник и все боковые ребра равны. На рисунках
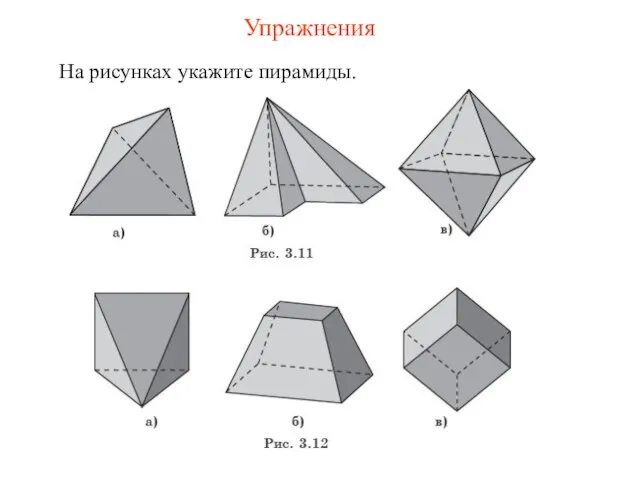
- 50. На рисунках укажите пирамиды. Упражнения
- 51. Сколько вершин (В), рёбер (Р) и граней (Г) имеет n‑угольная пирамида? Ответ: В = n +
- 52. Существует ли пирамида, которая имеет: а) 10 ребер? б) 6 рёбер? в) 24 ребра? г) 33
- 53. Какой многоугольник лежит в основании пирамиды, которая имеет: Ответ: 59-угольник. а) 8 рёбер? б) 22 вершины?
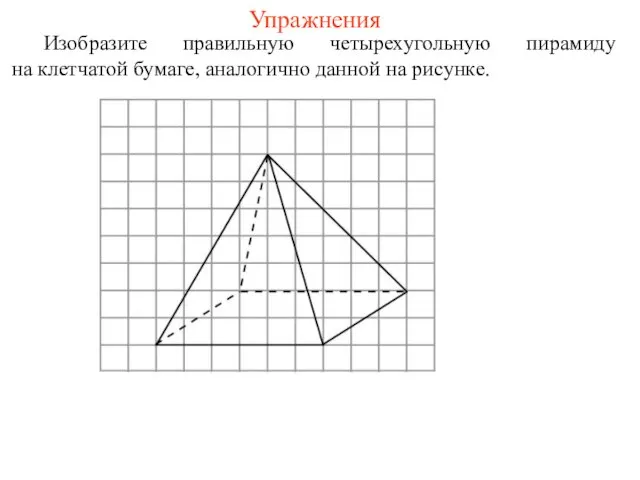
- 54. Упражнения Изобразите правильную четырехугольную пирамиду на клетчатой бумаге, аналогично данной на рисунке.
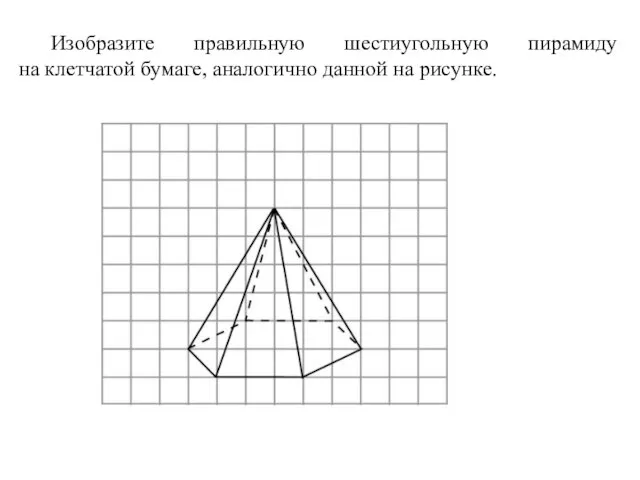
- 55. Изобразите правильную шестиугольную пирамиду на клетчатой бумаге, аналогично данной на рисунке.
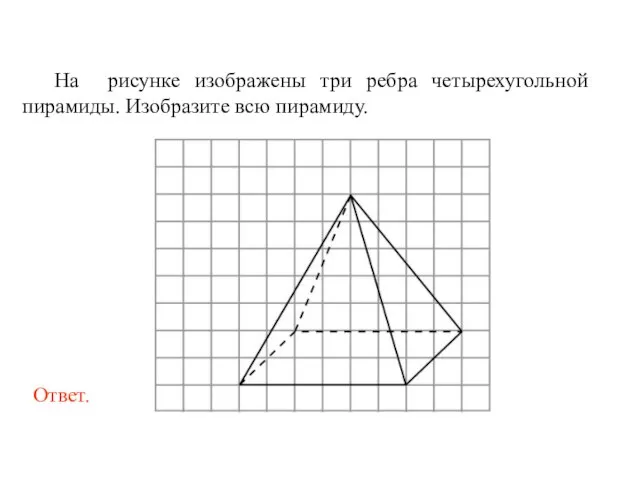
- 56. На рисунке изображены три ребра четырехугольной пирамиды. Изобразите всю пирамиду.
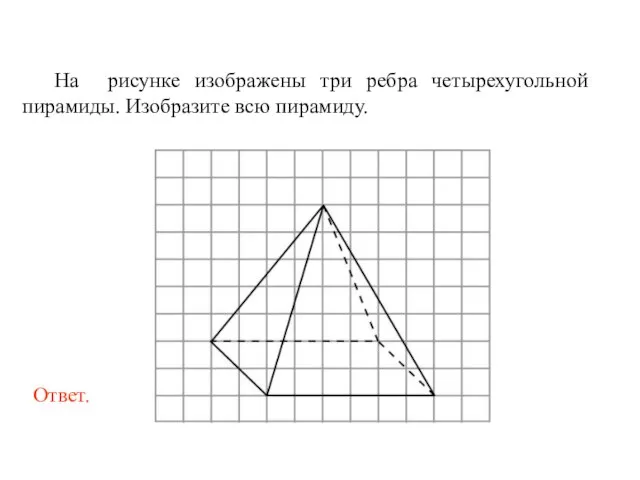
- 57. На рисунке изображены три ребра четырехугольной пирамиды. Изобразите всю пирамиду.
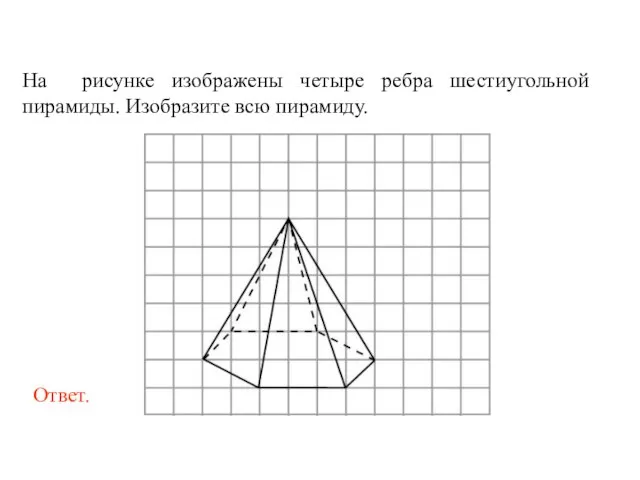
- 58. На рисунке изображены четыре ребра шестиугольной пирамиды. Изобразите всю пирамиду.
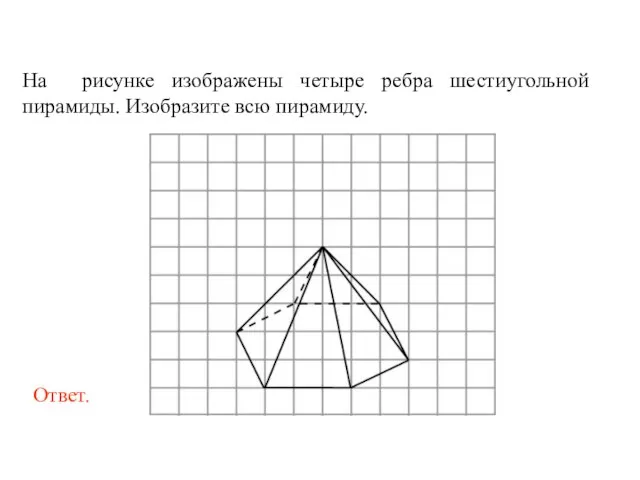
- 59. На рисунке изображены четыре ребра шестиугольной пирамиды. Изобразите всю пирамиду.
- 60. У многогранника шесть вершин и в каждой из них сходится четыре ребра. Сколько у него рёбер?
- 61. У многогранника двенадцать граней и все они пятиугольные. Сколько у него рёбер?
- 62. Существуют ли многогранник, у которого: а) 5 ребер? Нет. б) 6 ребер? Да, тетраэдр. в) 7
- 63. * Докажите, что у любого многогранника сумма чисел сторон всех его граней является чётным числом. Выведите
- 64. * Докажите, что у любого многогранника сумма чисел рёбер, выходящих из всех его вершин, является чётным
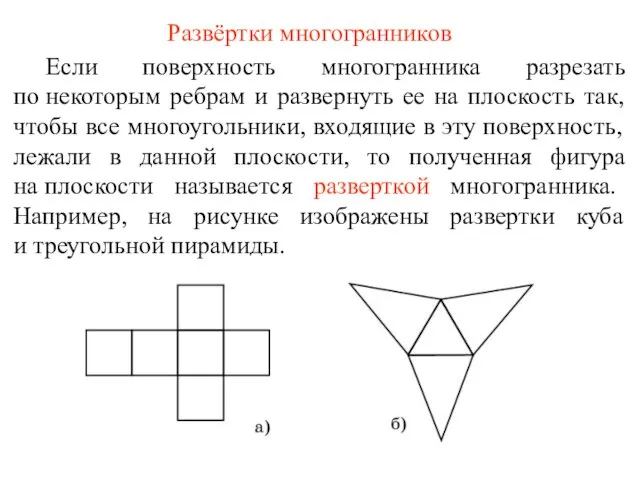
- 65. Развёртки многогранников Если поверхность многогранника разрезать по некоторым ребрам и развернуть ее на плоскость так, чтобы
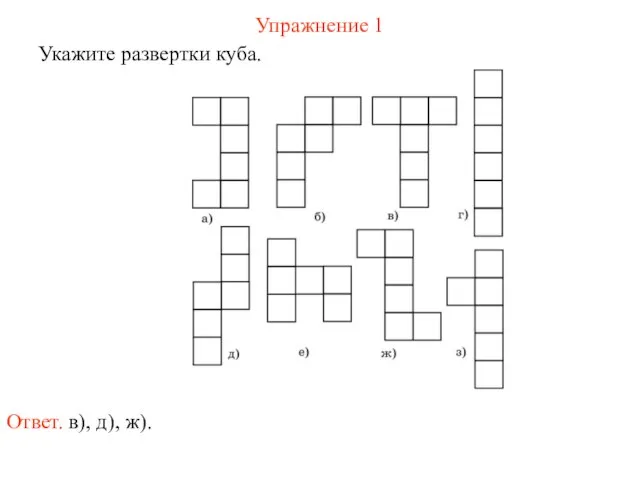
- 66. Упражнение 1 Укажите развертки куба. Ответ. в), д), ж).
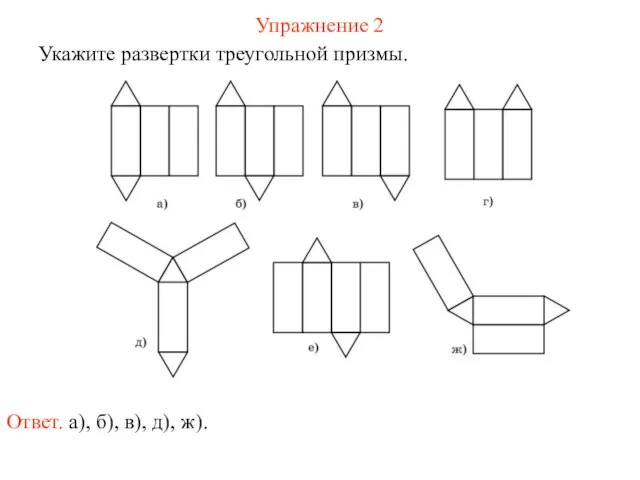
- 67. Упражнение 2 Укажите развертки треугольной призмы. Ответ. а), б), в), д), ж).
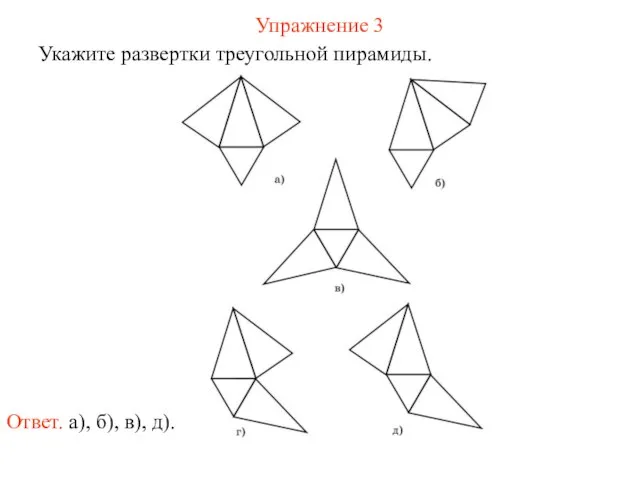
- 68. Упражнение 3 Укажите развертки треугольной пирамиды. Ответ. а), б), в), д).
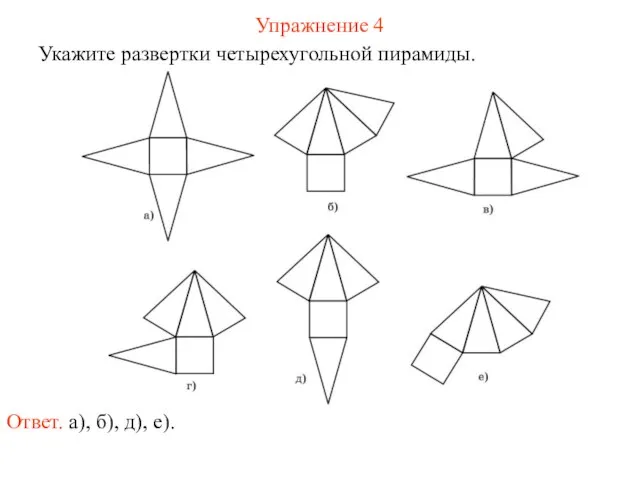
- 69. Упражнение 4 Укажите развертки четырехугольной пирамиды. Ответ. а), б), д), е).
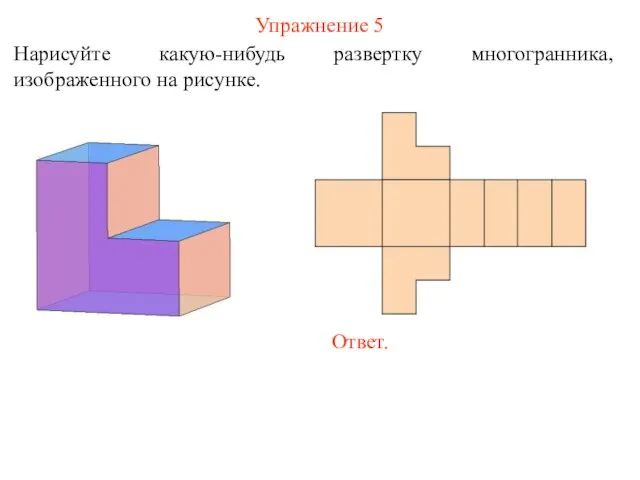
- 70. Упражнение 5 Нарисуйте какую-нибудь развертку многогранника, изображенного на рисунке.
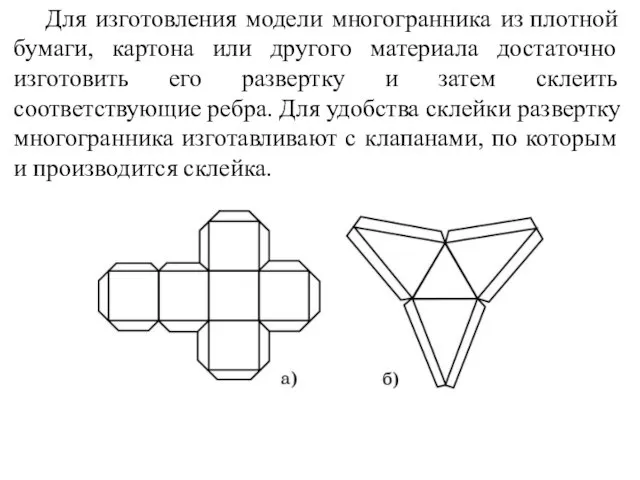
- 71. Для изготовления модели многогранника из плотной бумаги, картона или другого материала достаточно изготовить его развертку и
- 72. КУБ Для изготовления модели многогранника из плотной бумаги, картона или другого материала достаточно изготовить его развертку
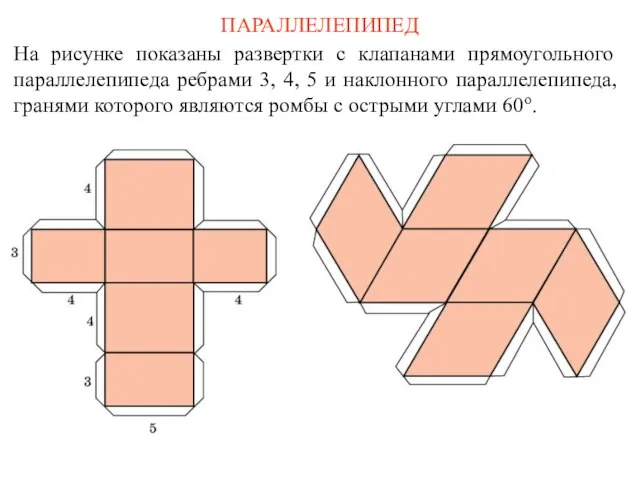
- 73. ПАРАЛЛЕЛЕПИПЕД На рисунке показаны развертки с клапанами прямоугольного параллелепипеда ребрами 3, 4, 5 и наклонного параллелепипеда,
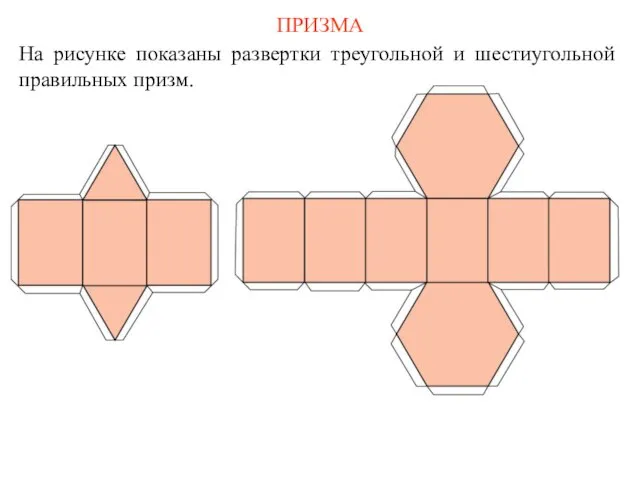
- 74. ПРИЗМА На рисунке показаны развертки треугольной и шестиугольной правильных призм.
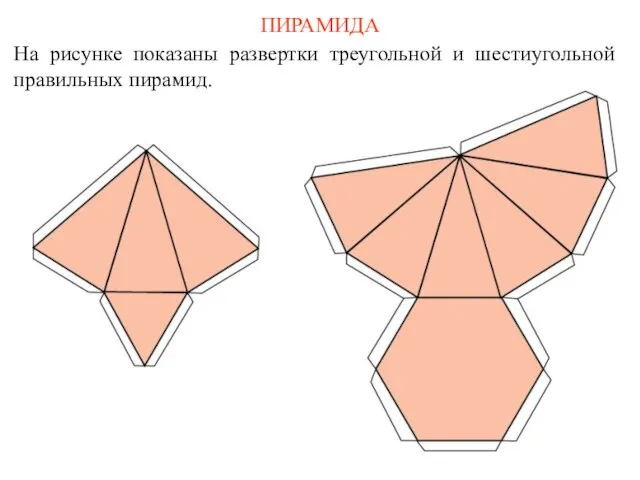
- 75. ПИРАМИДА На рисунке показаны развертки треугольной и шестиугольной правильных пирамид.
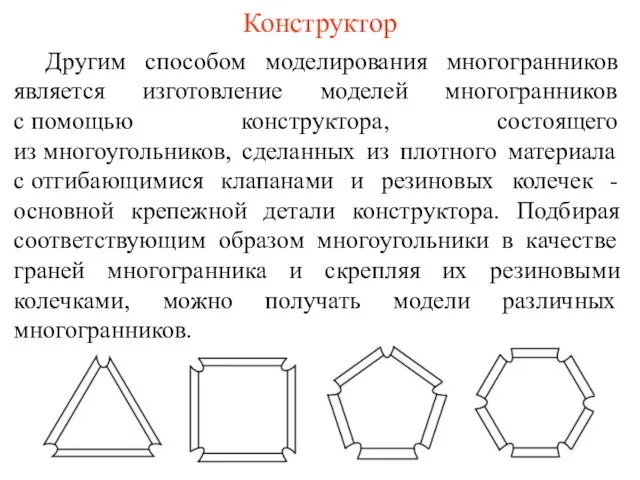
- 76. Другим способом моделирования многогранников является изготовление моделей многогранников с помощью конструктора, состоящего из многоугольников, сделанных из
- 77. Моделирование многогранников в программе GeoGebra Программа GeoGebra это свободно распространяемая программа, которую можно скачать с официального
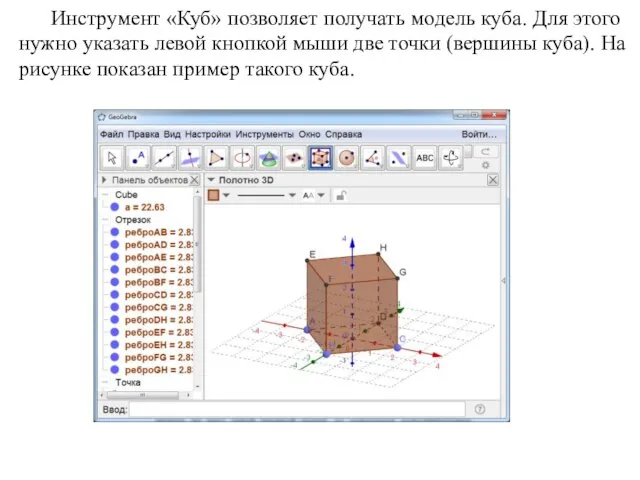
- 78. Инструмент «Куб» позволяет получать модель куба. Для этого нужно указать левой кнопкой мыши две точки (вершины
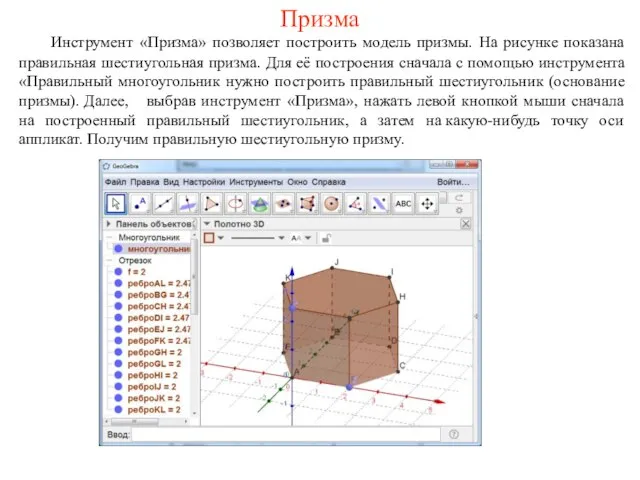
- 79. Инструмент «Призма» позволяет построить модель призмы. На рисунке показана правильная шестиугольная призма. Для её построения сначала
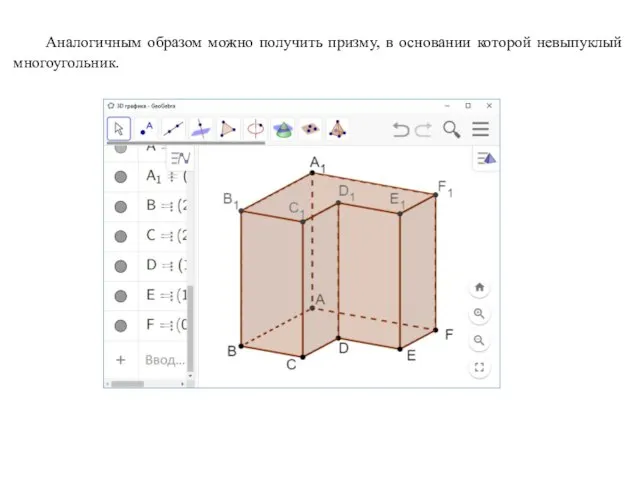
- 80. Аналогичным образом можно получить призму, в основании которой невыпуклый многоугольник.
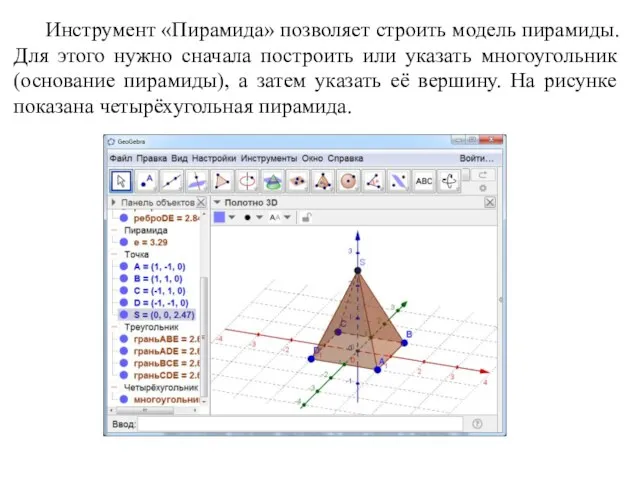
- 81. Инструмент «Пирамида» позволяет строить модель пирамиды. Для этого нужно сначала построить или указать многоугольник (основание пирамиды),
- 83. Скачать презентацию

























 Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Смешанные числа
Смешанные числа Задача из учебника Арифметика Леонтия Магницкого
Задача из учебника Арифметика Леонтия Магницкого Презентация на тему Теорема о сумме углов треугольника
Презентация на тему Теорема о сумме углов треугольника  В стране математики
В стране математики Презентация на тему СОСТАВ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА
Презентация на тему СОСТАВ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА  Перехідна та імпульсна перехідна функції
Перехідна та імпульсна перехідна функції Сигнальные карточки
Сигнальные карточки Математическая грамотность (7 класс)
Математическая грамотность (7 класс) Проценты. Счет и вычисления – основа порядка в голове
Проценты. Счет и вычисления – основа порядка в голове Множества и основные операции над ними
Множества и основные операции над ними Классификация видов моделирования систем
Классификация видов моделирования систем Трансформация координат и модели высоты
Трансформация координат и модели высоты Задача на тему: Прогрессия
Задача на тему: Прогрессия Единицы времени
Единицы времени Таблица истинности
Таблица истинности Словарь Владимира Ивановича Даля
Словарь Владимира Ивановича Даля Математический КВН
Математический КВН Четырехугольники
Четырехугольники Презентация на тему Конкретный смысл действия умножения (2 класс)
Презентация на тему Конкретный смысл действия умножения (2 класс)  Задания по математике для 3 класса
Задания по математике для 3 класса Теорема Пифагора
Теорема Пифагора Деление на 3
Деление на 3 Развертка. Создание объёмных фигур из плоскости
Развертка. Создание объёмных фигур из плоскости Способы построения параллельных прямых
Способы построения параллельных прямых Устный счет
Устный счет Аналитикалық геометрия
Аналитикалық геометрия Построение сечений
Построение сечений